Para explicar la estructura fina de los niveles de energía de los electrones en el átomo de hidrógeno, Uhlenbeck y Goudsmit [1] propusieron como hipótesis que el electrón, además de masa y carga, tenía un momento angular intrínseco (el espín) y por tanto un momento magnético. Pauli [2] introdujo la formulación matemática del espín en el contexto de la mecánica cuántica no relativista, asumiendo que sus valores son semienteros y que la función de onda tiene dos componentes, pero sin ofrecer una explicación de su origen. El origen «natural» del espín es la combinación de la relatividad y la cuántica en la ecuación de Dirac para el electrón [3]. La función de onda en mecánica cuántica es un vector en un espacio de Hilbert y la invariancia relativista ante transformaciones del grupo de Poincaré (el grupo inhomogenéo de Lorentz) requiere que las componentes de la función de onda pertenezcan a una representación irreducible de dicho grupo, como afirma el teorema de Wigner [4], que se basó en trabajos matemáticos previos (como los de Weyl [5]). Para una partícula de espín arbitrario, la ecuación cuántica relativista fue obtenida por Majorana (1932), Dirac (1936) y Proca (1936). Por tanto, una partícula tiene un espín s si la función de onda que representa sus estados tiene 2s+1 componentes (donde por componentes entendemos funciones de tipo espinor en el caso de espín semientero y funciones complejas en el caso de espín entero). Explicar el espín sin utilizar las matemáticas de la teoría de grupos aplicada a la mecánica cuántica es casi imposible, igual que lo es explicar el origen del momento angular en mecánica clásica.
¿Por qué el espín tiene las mismas unidades que el momento angular? Porque su origen es similar; el momento angular tiene su origen en la invariancia ante el grupo de rotaciones en el espacio de un sistema cuántico, por lo que la función de onda que lo representa debe ser una representación irreducible de dicho grupo. Las componentes del momento cumplen las leyes del álgebra de Lie so(3) asociada al grupo de Lie SO(3) de las rotaciones en el espacio. Las componentes del espín también cumplen las leyes de un álgebra de Lie, sl(2,C), asociada al grupo de Lorentz SO(1,3). Como el momento angular está asociado al grupo de rotaciones, su interpretación clásica como un «giro» es natural, sin embargo, dicha interpretación clásica para el espín no tiene sentido (salvo que hablemos de un «giro» en un espacio abstracto o espacio interno). En mi opinión, no ayuda nada a la intuición clásica el imaginar como «giros» las transformaciones de Lorentz entre sistemas de referencia inerciales; sin embargo, quizás ayude a algunos lectores, en dicho caso, hay que imaginar el momento angular y el espín como asociados a los «giros» tetradimensionales en el espacio de Minkowski.
Imaginar un electrón como una partícula «puntual» girando, aunque sea solo porque las unidades del espín son las mismas que las del momento angular, yo creo que no ayuda a la intuición clásica sobre su origen. En mi opinión, debemos aceptar que el espín es un concepto cuántico relativista sin análogo clásico no relativista. A mí me gusta decir que el espín está asociado al hecho de que la función de onda de una partícula relativista tiene varias componentes, es decir, el campo asociado a dicha partícula corresponde a varios «campos componentes» acoplados, como el campo electromagnético corresponde a campos eléctricos y magnéticos acoplados (o «unificados»). Mucha gente me dice que esta descripción es demasiado abstracta y no ayuda a su imaginación e intuición. Supongo que uno se acostumbra con el uso a este tipo de conceptos abstractos.
El teorema de Emmy Noether, que relaciona magnitudes físicas conservadas con la invariancia ante simetrías continuas (grupos de Lie) en un sistema físico (clásico o cuántico), nos muestra que el espín y el momento angular tienen un origen común. Por ello, sus unidades y sus propiedades son similares (sus componentes están evaluadas en un álgebra de Lie), por lo que se pueden sumar (dando lugar al llamado momento orbital).
De hecho, el operador de spín es un pseudovector (vector axial) como lo es el momento angular
, es decir, bajo rotaciones se comporta como un vector ordinario, pero no cambia ante simetrías (reflexiones especulares) en el espacio.
La función de onda de una partícula tiene
componentes indexadas por el valor del espín cuyos valores discretos son
(para una partícula de espín
), es decir, tiene un valor para cada punto del espacio
y para cada valor de la componente
del vector de espín
(donde
es la proyección ortogonal del vector de espín en dicho eje de coordenadas). Una partícula de espín cero tiene una función de onda con una sola componente
. Una partícula de espín 1/2 tiene una función de onda con dos «componentes»
y
. Y así sucesivamente. ¿»Componentes» entre comillas? La invariancia relativista de la ecuación de Dirac exige que la función de onda cuántica para un electrón tenga cuatro componentes en dos parejas, es decir, que sea un biespinor compuesto de dos espinores. En general, las componentes de la función de onda para partículas de espín semientero son espinores, a diferencia de las componentes «vectoriales» de las de espín entero. Esta diferencia, de origen matemático debido a las leyes de la relatividad combinadas con la mecánica cuántica, parece extraña y casi imposible de entender a quien ignora los detalles matemáticos. Un físico lo único que puede decir es que la Naturaleza es así. Mientras no tengamos una explicación a por qué la Naturaleza es cuántica y relativista no podremos explicar el origen último de estas propiedades. En el momento presente aún estamos muy alejados de poder entender por qué la Naturaleza es cuántica y relativista.
¿Por qué la función de onda tiene que ser descrita mediante una representación de un grupo? El principio más fundamental de la mecánica cuántica es que los estados de un sistema forman parte de un espacio de Hilbert (un espacio vectorial con un producto interior que es completo). No sabemos por qué, pero así es la Naturaleza. La descripción matemática de la acción de un grupo de simetría sobre un espacio de Hilbert requiere utilizar una representación, es decir, requiere describir las transformaciones del grupo como matrices que se multiplican por los vectores del espacio de Hilbert. La teoría de la representación de grupos es muy abstracta, pero su importancia es capital en física cuántica. En matemáticas, una representación de un grupo G es un homomorfismo de G en el grupo D(G) cuyos elementos son operadores en una espacio vectorial L (eligiendo una base de L los elementos de D(G) son matrices); L es el llamado espacio de representación y su dimensión es el grado (o dimensión) de la representación de D(G). Hay muchos tipos de representaciones de grupos, pero en física cuántica se utilizan representaciones unitarias, en las que las matrices son unitarias (matrices cuya inversa es igual a su adjunta conjugada y que preservan el producto interior del espacio de Hilbert).
Dado un campo, sea , dos observadores en sendos sistemas inerciales conectados por una transformación de Lorentz-Poincaré
(en componentes
) deben observar el mismo campo
; la covariancia relativista exige que el campo (es decir, la física) sea el mismo, aunque sea observado desde puntos de vista diferentes. Sin embargo, no tiene por qué cumplirse que
. En general, si el campo
tiene varias componentes, dichas componentes podrán «mezclarse» haciendo que
, donde
es una matriz que «representa» la transformación de Lorentz-Poincaré
; en componentes podemos escribir que
. El tipo y las propiedades de las matrices
depende del grupo de simetría considerado; para el grupo de Lorentz-Poincaré dichas matrices están caracterizadas por una propiedad, el espín, que relaciona las propiedades de estas matrices con el número de «componentes» del campo. La teoría de la representación de grupos de simetría se desarrolló a principios del s. XX junto a la mecánica cuántica (su nicho natural), aunque sus orígenes se pueden encontrar en la segunda mitad del s. XIX cuando los matemáticos estudiaron los orígenes de la geometría y su relación con los grupos de simetría.
Profundizar en estas cuestiones matemáticas quizás nos llevaría demasiado lejos. Cuando la gente me pregunta por qué los físicos no saben explicar con palabras sencillas lo que es el espín, yo suelo contestar que entender el espín es tan difícil como entender el momento angular. Hay libros enteros dedicados al momento angular, sus propiedades y cómo operar con él en sistemas multipartícula (algunos ejemplos en Google Books). No es fácil manejar el momento angular y el espín utilizando la intuición física clásica, por lo que la mayoría de los físicos trabajamos estos conceptos de forma operativa, obviando imágenes que nos confundan. Con el uso uno acaba teniendo la sensación de que los entiende, pero quizás sea solo una ilusión. Lo que debe quedar claro al lector es que las reglas matemáticas para manejar el momento angular y el espín en los cálculos están perfectamente claras y que, además, no existe ninguna analogía clásica que reproduzca todas y cada de una de estas reglas matemáticas; en los últimos 90 años ningún físico y ningún matemático ha logrado una analogía clásica adecuada que permite entender al lego estos conceptos tan abstractos y a la vez tan importantes. Repito, todas las analogías clásicas fallan (al menos las que yo he podido leer). Por cierto, hay algunas analogías clásicas «buenas» para ciertos valores del espín, pero no funcionan para todos.
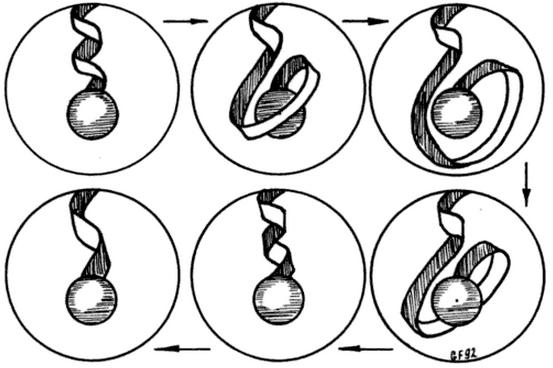
Para finalizar, las figuras que acompañan esta entrada corresponden al «truco del cinturón de Dirac» (también llamada «cinta de Dirac») para explicar por qué un electrón tiene que «girar» 720 grados para recuperar su estado original (cuando para un objeto clásico basta un giro de 360 grados). Hay muchos vídeos de youtube, pero a mí me gusta el siguiente (que no explicaré en detalle). Os animo a profundizar usando Google, si os apetece.
Algunas referencias clásicas:
[1] Naturwissenschaften 13: 953-954, 1925; Nature 117: 264-265, 1926.
[2] Zeitschrift für Physik 43: 601-623, 1927.
[3] Proc. Roy. Soc. Lond. A 117: 610-624, 1928; Proc. R. Soc. Lond. A 118: 351-361, 1928.
[4] Gruppentheorie (Friedrich Vieweg und Sohn, Braunschweig, Germany, 1931), pp. 251-254.
[5] Math. Zeitschrift 23: 271-309, 1925; Math. Zeitschrift 24: 328-376, 1926; Math. Zeitschrift 24: 377-395, 1926; Math. Zeitschrift 24: 789-791, 1926.
NOTA: Las dos figuras que abren esta pieza son de George K. Francis (ResearchGate), autor de «A Topological Picturebook,» Springer (1988).



Cierto es…La manera más simple de «imaginar» el espín es como una coordenada «interna» adicional que es necesario especificar en el espacio-tiempo. Un número y que interpretamos como algún tipo de rotación es un espacio interno de la propia partícula. A diferencia de las coordenadas usuales (que toman cualquier valor real), el espín es una «dimensión» que sólo toma (aparentemente y excepción hecha de la representación de espín continuo de Majorana que generalmente se descarta) valores discretos. Las representaciones unitarias irreducibles del grupo de Lorentz o del de Poincaré tienen muchas sutilezas (está también la representación del campo de «infinitas componentes» de Majorana, de la que hay poco escrito en general, pese a que Wigner redescubrió el trabajo de Majorana sobre ese punto: las representaciones unitarias infinodimensionales del grupo de Poincaré).
Está bien el artículo, aunque personalmente esas representaciones pictóricas para el espín 1/2 siempre me han parecido artificiales, dado que no conecemos en nuestra experiencia cotidiana usual de algo «normal» (aparentemente) que para volver a ser igual tenga que girarse 720 grados sexagesimales. Las tijeras de Dirac o equivalentemente el truco del libro y el vaso que hay que pasarse acrobáticamente «sobre uno mismo» sirven para visualizar el concepto, pero esconde mucho de lo que hay detrás del espín 1/2 (intrínsecamente cuántico). Yo aún no he visto jamás algún ejemplo «más simple» sobre cómo visualizar eso. Quizás no pueda hacerse. Del espín 3/2 tampoco he visto nada (es que pensar en algo que lo giras ¿cuánto sería en ese caso?Porque si el gravitón es igual si giramos 180 grados … ¿Serían 270 el campo de Rarita-Schwinger? No es «natural» en las analogías el espín semientero, se resiste a cualquier cosa «simple» hasta ahora), pero sí recuerdo en cierto libro de divulgación ejemplos de espín cero, uno y hasta 2 con imágenes de ciertas cartas de una baraja francesa. Es que los espines semienteros se atragantan en nuestra «percepción ordinaria» aunque algún día espero dar con algo para entenderlos de forma «intuitiva y transparente» y no tan abstracta (que parece ser la única hasta ahora, bien con estas construcciones, bien con trucos como la representación de Majorana-Penrose).
Una reciente entrada en TRf enrollandose en el giro del electrón:
http://motls.blogspot.com.es/2012/12/the-electron-is-spinning-after-all.html
Si, yo también la leí. Es curioso el Sr. Motl, él sí que cree que el spin corresponde en verdad a un giro interno de la partícula (mejor dicho: cuerda).
me encantan este tipo de entradas, nos permiten intuir los vericuetos de las discusiones de la física teórica. Sin llegar a pedir analogías sobre lo que es el espín, ¿qué pasaría si los estados de un sistema cuántico no formaran parte de un espacio de Hilbert, o formaran parte de un espacio vectorial no Hilbert, si es que eso existe?
CreatingClouds, para que la función de onda (vector en el espacio vectorial) sea interpretada como amplitud de probabilidad y las probabilidades de todos los estados posibles sumen la unidad es necesario que sea un espacio de Hilbert. Si fuera algo muy parecido, como un espacio prehilbertiano (cuyo producto interior no es completo) en ciertos sistemas cuánticos las probabilidades de todos los estados posibles no sumarían la unidad. Desde un punto de vista probabilístico no tiene sentido.
La unitariedad es natural en toda teoría natural física. Que no se conserve la probabilidad en un sentido es totalmente no físico.
Lo que son las interpretaciones… viendo a la señorita danzando con esos vasos me recordó a lo que veían los antiguos egipcios en la constelación Taweret (osa mayor).
Sobre interpretaciones, ví un vídeo de Feynman hace unos días en el que decía lo siguiente (con mis propias palabras):
Para nosotros son naturales la fuerzas de contacto entre objetos, y cuando hablamos de fuerzas a distancia a los menos acostumbrados a ellas, a veces se recurren a analogías como los muelles simulando la interacción para que consigan entenderlas… cuando es todo lo contrario, son las fuerzas de contacto las que son consecuencia de las fuerzas a distancia (electromagneticas de repusión). Entonces, ¿porqué hemos de esforzarnos en explicarles las fuerzas a distancia a partir de cosas conocidas, en vez de explicarles las cosas conocidas a partir de las fuerzas a distancia, que es como relamente funciona la naturaleza?
Sucede lo mismo con el espín o cualquier otra cosa cuántica. Los fenómenos cuánticos no es que no los entendamos, los entendemos muy bien, lo que pasa es que es así como funciona el universo, no como nosotros lo vemos a gran escala (es como comparar macroeconomía y microeconomía, el macroeconomista sabe que en el fondo, todo se mueve de acuerdo a las reglas de la microeconomía, fundamentalmente que cada individuo busca su propio beneficio). Entonces creo que no hay que enfocarse en hacer entender a la gente cosas cuánticas a partir de cosas conocidas, ya que al final pensarán que son cosas muy raras que no tenemos claro como explicar, sino que hay que explicarles las cosas conocidas a partir de las cosas cuánticas.
El spin es una de esas propiedades en las que más claramente se manifiesta la cada vez más difusa linea que separa matemáticas y realidad. Las matemáticas nos permiten describir de forma increíblemente precisa fenómenos totalmente diferentes y separados por un rango de escala enorme, nos permiten captar las simetrías fundamentales, predecir nuevos fenómenos y «explicar» como funciona la naturaleza en su nivel fundamental. El «problema» en estos casos es que la «explicación» que obtenemos no está basada en las cosas cotidianas a las que el cerebro está acostumbrado y para las que ha sido diseñado por la evolución sino que está basada en estructuras matemáticas abstractas como la función de onda, los spinors o los vectores en espacios de Hilbert. Por tanto parece lógico preguntarse: si estas estructuras matemáticas describen tan fielmente la realidad ¿es porque son reales? Si no son reales ¿como se explica su enorme eficacia al describir nuestro Universo? Si son reales ¿Que son? ¿Donde están?
¿De que están hechas? Quizás sea necesario cambiar la definición misma de realidad. En el caso del spin se ha medido físicamente un momento angular intrínseco en las partículas por lo tanto parece que algo está girando pero ¿Que es lo que gira? ¿Es un punto sin dimensiones o es algo como una esfera? Evidentemente estas preguntas surgen de nuevo de nuestra necesidad de hablar de los fenomenos cuánticos en términos de algo cotidiano y eso es imposible, sin embargo, quizás algunas de las preguntas se podrían explicar en términos de dimensiones ocultas del espacio (los espacios internos de las partículas), quizás el spin es una prueba de la existencia de esas nuevas dimensiones o quizás todas estas preguntas no tengan siquiera sentido dentro de la física o esten fuera de nuestra capacidad de conocimiento. Personalmente, desde mi punto de vista inexperto siempre me ha parecido que podría haber una conexión entre los números complejos y algún tipo de dimensión oculta del espacio.
«¿De que están hechas? Quizás sea necesario cambiar la definición misma de realidad. En el caso del spin se ha medido físicamente un momento angular intrínseco en las partículas por lo tanto parece que algo está girando pero ¿Que es lo que gira? ¿Es un punto sin dimensiones o es algo como una esfera?»
Hola Planck, tus reflexiones me parecen muy interesantes. Yo creo que los tiros podrían ir por las dimensiones ocultas que ya comentas y que lo que gira no es un punto ni una bola sino una cuerda o brana (= el electrón), en varias dimensiones (esperemos que 11)
Saludos
Podría ser Pablo, de hecho creo que algunos físicos identifican algunas de las dimensiones extra de la teoría de cuerdas con esos espacios internos en los que parecen actuar las partículas (como el espacio en el que actua el spin).
Confundir la herramienta matemática con la realidad fue el error de los pitagóricos, fue también el error de platón, que nos llevó al descarrilamiento, haciéndonos creer que el espíritu tienen existencia real objetiva y finalmente es el error de Hegel que confunde el método con la materia de estudio.
La matemática implicada para explicar el espín, es necesaria para poder tener una construcción teórica de utilidad, ahí en su campo acotado, es paradójicamente, una explicación simplista, de una realidad muy compleja.
Las teorías físicas, que no se nos olvide, son producciones creativas de un ser vivo con un cerebro, con las adaptaciones necesarias para la sobrevivencia. La física y la matemática son construcciones mentales… no es la realidad.
Me temo que el tema es más complejo que eso, física y matemáticas están absolutamente ligadas, sino fíjate en el debate sobre la existencia ontológica o epistemológica de la función de onda cuántica. Las teorías físico-matemáticas son construcciones mentales abstractas pero que reflejan la coherencia interna de la naturaleza (sus leyes fundamentales), estas no son la realidad en si misma pero son un «reflejo» de ella y representan las relaciones entre las magnitudes físicamente medibles (la realidad). La función de onda en si misma no es medible físicamente aunque contiene toda la información física (medible) de un sistema cuántico sin embargo, los observables (representados por operadores hermíticos que operan en espacios de Hilbert) que están incluidos en la función de onda si corresponden a magnitudes físicas medibles pero solo podemos medir la cantidad definida por el operador hermítico que representa la proyección ortogonal de la función de onda sobre el subespacio de Hilbert asociado al autovalor que queremos medir, o sea la probabilidad de hallar el observable al hacer una medida. ¿Realmente no ves que física, matemáticas y realidad están inextricablemente unidas?
O sea, que los legos en la materia debemos desistir de entender algo si no tenemos preparación matemática suficiente. Ya hace un tiempo que no leo nada sobre física y creo que en parte es por el convencimiento de haber llegado al límite de lo que puedo entender sin la ayuda de falsas analogías.
No sé si la matemática es real o no, pero es evidente que sin dominar la matemática no entiendes la física, del mismo modo que el présbita, el miope y el hipermétrope no ven un carajo sin la ayuda de las lentes. Sobre la realidad o irrealidad de la matemática tenemos que a) es irreal e inaccesible a la razón humana, b) es virtual pero accesible a la razón humana, y c) es real y por tanto accesible a la razón humana. Los supuestos b y c falsan el supuesto a, pero de lo que se trata, al menos en mi opinión, es enfatizar que sin el dominio de la herramienta matemática no es posible entender la física.
Encontrarle una “métrica” a las matemáticas fue uno de los problemas del milenio que David Hilbert propuso en su día a la comunidad matemática. Supongo que conoces la conclusión a la que llegó Gödel con sus teoremas de incompletitud. Aunque en realidad el programa de Hilbert consistía en encontrar un formalismo lógico y consistente para la matemática, lo de “métrica” es una licencia que me tomo. ¿Entes matemáticos, dimensiones matemáticas? Ni idea, no platonicemos mucho no sea que venga uno a llamarnos descarriados ;-D