¿Por qué aprender a jugar bien al ajedrez es tan difícil? Un nuevo estudio afirma que la razón podría ser que la dinámica del aprendizaje por refuerzo de estos juegos bipersonales es caótica (está caracterizada por un atractor extraño). Las estrategias de juego aprendidas se comportan como órbitas (trayectorias) del sistema dinámico y son impredecibles debido su gran sensibilidad a los detalles del proceso (pequeños cambios en el proceso de aprendizaje conducen a grandes cambios en el resultado final) ). El estudio de Tobias Galla (Universidad de Mánchester, GB) y J. Doyne Farmer (Universidad de Oxford, GB; Instituto de Santa Fe, Nuevo México, EEUU), publicado en PNAS, ha consistido en la simulación por ordenador de miles de juegos de dos jugadores en los que se simulaba la toma de decisiones propia de una persona. Obviamente, eran juegos muy sencillos, pero los autores creen que si se observa la dinámica caótica para juegos tan sencillos también se debería observar en juegos más complejos (como el ajedrez o el póker). Como siempre, el nicho natural de la teoría de juegos son los mercados financieros, por ello los autores creen que su estudio podría tener implicaciones socioeconómicas; quizás los mercados son impredecibles debido a que aprender cómo evolucionan está controlado por una dinámica caótica. El artículo técnico es Tobias Gallaa, J. Doyne Farmer, «Complex dynamics in learning complicated games,» PNAS 110: 1232-1236, Jan 22, 2013. Vía «Una explicación científica para la imposibilidad de dominar por completo algunos juegos,» CORDIS, Jan 11, 2013.
7 Comentarios
Deja un comentario
Por Francisco R. Villatoro, publicado el 11 febrero, 2013
Categoría(s): Ciencia • Matemáticas • Mathematics • Noticias • Science
Etiqueta(s): Ajedrez, Ciencia, Economía, Física computacional, Matemáticas, Noticias, PNAS, Póker, Teoría de juegos
⇦ Un motor magnético muy atractivo, aunque no sea un móvil perpetuo • Ya han finalizado las colisiones protón-plomo en el LHC del CERN ⇨
Categoría(s): Ciencia • Matemáticas • Mathematics • Noticias • Science
Etiqueta(s): Ajedrez, Ciencia, Economía, Física computacional, Matemáticas, Noticias, PNAS, Póker, Teoría de juegos
⇦ Un motor magnético muy atractivo, aunque no sea un móvil perpetuo • Ya han finalizado las colisiones protón-plomo en el LHC del CERN ⇨


Me encantó
Uhm! No sé qué decir, pero yo estaba convencido de que los límites al aprendizaje de este dichoso juego lo establecen principalmente:
a) La dedicación (jugar muy bien al ajedrez, quiero decir por encima de la ratio ELO 2000, equivale en cierto modo a tocar bien un instrumento musical).
b) Una enseñanza guiada por un maestro de nivel. Los libros, como es obvio, no detectan los posibles «vicios» del alumno.
c) La capacidad necesaria, algo así como el don nativo para combinar.
Yo he querido al ajedrez más de lo que el ajedrez me ha querido a mí. En su tiempo podía jugar a ciegas y ganaba contra aficionados. Pero ahora no paso de los 1850 ELO, y, lo que es peor, no soy capaz de intuir qué diablos hay en la cabeza de un jugador de rango superior. No sé cómo discurren sus estrategias, y si alguna vez lo he preguntado, al parecer tampoco el jugador de nivel es muy consciente de ello.
Está claro, por otra parte, de que las estrategias en ajedrez pueden resultar de combinaciones tácticas a gran profundidad. Esto lo ponen en evidencia los programas de jugar al ajedrez, que desde hace años baten (basados en PC) a los campeones del mundo, y cuyos algoritmos se basan en lo que se llama «la fuerza bruta», es decir ir podando el árbol de combinaciones valorando según criterios no muy sofisticados (valor de las piezas, casillas amenazadas, etc.).
Concedo la intervención del proceso caótico en el caso en que se aprende exclusivamente por experiencia, es decir en base a partidas entre aficionados. Pero ese no es el modelo ideal. En la URSS, por ejemplo, el ajedrez formaba parte del aprendizaje temprano, y los alumnos aventajados se seleccionaban y eran invitados a trabajar duro, aleccionados por maestros de gran nivel. Aunque yo creo que en mi caso, ni así.
Pones al mismo nivel el ajedrez y el poker. Mi opinión es que el segundo es un juego de azar.
El artículo dice que lo caótico es el aprendizaje del ajedrez o el póker, no los juegos en sí.
No he leído el artículo original, pero la recensión de CORDIS me parece un poquito amarilla.
Yo creía saber que Arthur Samuel (http://infolab.stanford.edu/pub/voy/museum/samuel.html) ¡en la década de 1950! aplicó -sin saberlo- técnicas de aprendizaje por refuerzo al juego de las damas y consiguió un programa que jugaba bastante bien. Yo creía saber que G. Tesauro, aplicando técnicas de aprendizaje por refuerzo, consiguió en los 90 que su programa de backgammon fuera el jugador más potente del mundo. Y, aunque no soy un experto, creía saber que el aprendizaje por refuerzo se había aplicado con cierto éxito al ajedrez (http://www.cs.princeton.edu/courses/archive/fall06/cos402/papers/chess-RL.pdf) y que incluso se estaba intentando aplicar al Go (http://www.incompleteideas.net/sutton/papers/silver-sutton-mueller-12.pdf).
Pero quizás todo esto eran tonterías y lo importante es hablar de caos y atractores… si lo pudiéramos mezclar además con evolucionismo y cambio climático, ¡sería la bomba!
Sin animo de incordiar al resto me parece que es muy legitima la aproximación dada. Existe la posibilidad que termine demostrándose incorrecta, para eso estamos en ciencia, pero lo que si entreveo, a titulo personal eso si, es que en nada des legitima a otras aproximaciones. Mi humilde valoración es que es simplemente otra óptica a la misma realidad. Puede que las técnicas por refuerzo sean efectivas pero puede que esta aproximación de la explicación del porque no son tan efectivas como debieran, por ejemplo. No se si me he explicado bien.
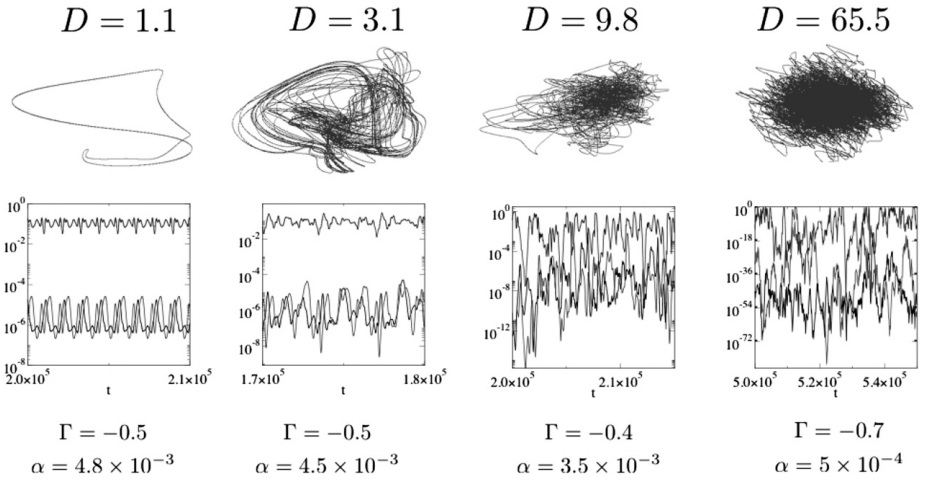
Las gráficas por si solas no explican la pregunta. Sería bueno que se describiera los eje de coordenadas que representan y los valores de alfa. Ya que no se sabe que variables se están trabajando y por lo tanto la interpretación se hace imposible para cualquier persona si ya para una persona que sabe de matemáticas y de funciones se hace imposible.