La edición de 2013 del catálogo de revistas con índice de impacto de Thomson Reuters (llamada JCR 2012, por Journal of Citation Reports) comprende 10.853 revistas clasificadas en 232 categorías en sus ediciones de Ciencia (Science JCR) y Ciencias Sociales (Social Sciences JCR); entre ellas, 379 reciben por primera vez su índice impacto. Además, 33 han salido fuera del JCR 2013 respecto al JCR 2012, es decir, han dejado de ser revistas con índice de impacto. Publicado desde 1975, el JCR continúa siendo utilizado para clasificar las revistas científicas (y con ellas los propios artículos) en «buenos» y «malos» a la hora de evaluaciones (como la de los sexenios en España).
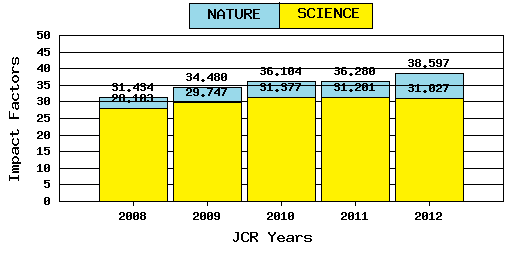
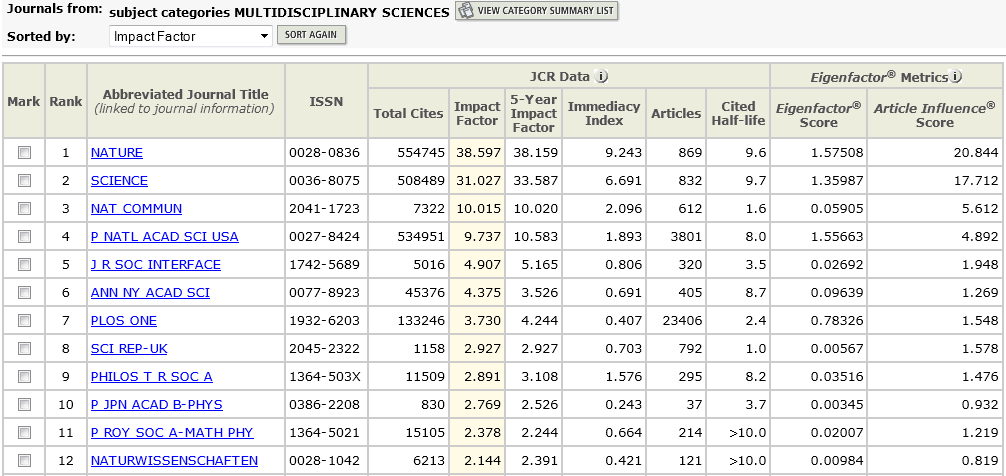
La figura que abre esta entrada muestra las 12 revistas con mayor índice de impacto. Obviamente, no tiene sentido dicho listado, pues el factor de impacto depende del área. Sin embargo, muchos se sorprenderán de que no esté Science cerca de Nature. En el JCR 2013, Science ocupa el lugar número 20 con 31,027, mientras Nature mantiene un honroso puesto número 7 con 38,597. En el último lustro Nature siempre ha estado por encima de Science y además ha logrado incrementar su distancia.
En el campo de las revistas multidisciplinares, PNAS ocupa el cuarto puesto y PLoS ONE baja su índice de impacto (casi seguro que por haber publicado demasiados artículos; de hecho, 13781 en 2011 y 6722 en 2010).
España tiene 75 revistas impactadas en el JCR 2012 y en esta figura tienes las 12 primeras por factor de impacto. No quiero enrollarme más con este asunto.
Entre las 33 revistas que han desaparecido (que en 2012 no tendrán factor de impacto, pero que podrían recuperarlo y tienen 2 años para ello) me gustaría destacar cuatro que afectan a colegas cercanos: International Journal of Computational Intelligence Systems, Journal of Database Management, Journal of Parallel and Distributed Computing, y Mobile Information Systems. También me gustaría destacar la desaparición de la Revista Clinica Espanola.
Por cierto, en las áreas en las que yo publico estoy contento porque todas las revistas en las que he publicado en 2012 han subido de factor de impacto respecto al de 2011. Así que estoy de enhorabuena.
Bueno, no os aburro más. Que sepáis que los que publicáis de forma asidua tenéis que daros un paseo por el nuevo JCR 2012.




Gracias por la noticia, este año se me pasaba. Por cierto, entre las desaparecidas está afortunadamente «ENERGY EDUC SCI TECH» (ISSN 1301-8361), una estafa turca con IF = 31.677 dedicada a publicar prácticamente sólo a turcos y con un 80-90% de autocitas. Veo que el sistema funciona.
aqui os dejo un link para consultas
http://wokinfo.com/products_tools/analytical/jcr/
Lo gracioso de las revistas de impacto es que, como alguien se el ocurra publicar un novedad sobre algo firmemente establecido (pongamos por ejemplo el teorema de Pitágoras), es obvio que no va a encontrar ninguna referencia (como no sea un libro de texto) que poder citar. Pues bien, en la revistas de impacto, como no dores la píldora a unos cuantos investigadores de tu área (muchas veces sin venir a cuento), simplemente no publicas.
No es cierto, Bruno, si tu novedad es una «buena» o «bonita» sorpresa sobre algo bien conocido, será muy fácil de publicar. El problema es que tu «novedad» no sea ninguna novedad, sino una simple «chorrada» para los expertos, entonces te será muy difícil publicarlo. No tienes que dorar la píldora a nadie, sólo tienes que hacer bien tu trabajo. Un buen trabajo siempre se publica fácil. Lo díficil es publicar «basura» (aún así, hay mucha «basura» que acaba siendo publicada porque el sistema no es perfecto).
¡Dios te oiga!, pero me consta que no es así, no por experiencia propia, sino por referencia (muy fiables) de terceros, sobre un trabajo interesante y coherente, relacionado con la teoría de los números complejos, que ya me dirás qué referencias se pueden citar en ese terreno, cuando posiblemente fuese Gauss el último en trabajar en ella.
Perdona, Bruno, pero sobre los números complejos hay miles de artículos publicados todos los años en la actualidad. Muchos amigos míos trabajan en Análisis Complejo y es un campo de las matemáticas muy activo y en el que sigue habiendo muchas cuestiones abiertas.
«incredible claims require incredible evidences». Y si las evidencias están ahí te aseguro que la revista se lo pensará dos veces antes de hacer el ridículo y dejar escapar el pescado.
Por otra parte, también se arriesgan a hacer el ridículo si las evidencias no son tales (están mal demostradas o incompletas) o si repiten resultados ya publicados (recuerdo el ig-nobel de la cola de caballo nada menos que en PRL, que Francis nos contó que ya estaba resuelto). Si no eres capaz de delimitar bien el campo de trabajo en el que te has basado y demostrar cierta inquietud en buscar resultados parecidos o las implicaciones que tendría el resultado (que lo haría indudablemente visible a la comunidad científica), les va a resultar muy difícil a los editores determinar si hay novedad o si no es incluso una trivialidad.
Supongo que lo que se entiende por comunidad científica no se ciñe en exclusiva a los papers publicados, hay científicos (físicos, matemáticos, etc.) que trabajan aislados o en grupos reducidos que comparten episteme y fórmulas incluso sin publicarlas. También se da el caso de autores que no publican porque uno con más autoridad aconseja no hacerlo. O imaginemos las sesiones informales de dos, tres o cuatro físicos que se reúnen en torno a una mesa a cuadrar ecuaciones cotejando sus resultados y cuyo objetivo principal no se halla en publicar sino en el placer de la investigación. Hay un flujo de información considerable que se establece entre científicos particulares que no siempre se extiende a la comunidad científica por razones diversas pero cuyo valor es incuestionable. Es decir, son intangibles que dependen en buena medida del carisma de uno o varios científicos y que tienen el mismo valor (para ellos) que la publicidad que otorga un paper. Además, la mayor o menor calidad de un paper está sometida a crítica, y no es raro que se produzcan batallas crueles por reivindicar tal o cual teorema, batallas que crean enconos y rencores y que pueden atascar el despliegue de ciertos asuntos a investigar. Las revistas científicas no trabajan con intangibles ni con carismas, en este sentido tratan de ofrecer una información objetiva y un marco de consenso que posibilita el avance de la ciencia, lo que me parece bien. Pero hay otros aspectos de la cuestión que van más allá de los criterios canónicos para decidir lo que es valioso y lo que no lo es.
Artemio, la ciencia no publicada no es ciencia (puede ser «paraciencia» pero nunca ciencia). La ciencia es el acervo común que está publicado por los llamados científicos. Lo no publicado no pertenece a dicho acervo y por tanto no es ciencia. Quien afirme que hace ciencia sin publicar nada se engaña a sí mismo. Otra cosa es que pretenda publicar su trabajo en el futuro y durante cierto tiempo trabaje en solitario; pero para convertir en ciencia su trabajo debe publicarlo y debe recibir el consenso de la comunidad. Sin consenso de la comunidad científica no hay ciencia posible.
Bruno, un apunte tangencial a tu comentario. El número complejo puede representarse como la suma de un número real y un número imaginario, que es un múltiplo real de la unidad imaginaria y que se indica con la letra i. Los números imaginarios se usan habitualmente por los físicos teóricos, en particular por los teóricos de cuerdas. Los cuerdistas tienen que describir el hiperespacio (un espacio con muchas dimensiones) y para ello les resulta más fácil trabajar con números imaginarios como la raíz cuadrada de menos 1. Los desarrollos matemáticos de esta forma de proceder conducen a resultados paradójicos tal que a.b = -b.a, un resultado que no casa con los números ordinarios. Esto quiere decir que los números complejos se han desarrollado bastante en el campo de la física teórica, aunque supongo que los papers publicados sobre este asunto no ponen el énfasis en la mutación que ha sufrido la matemática gaussiana sino en los aspectos aparentemente hiperdimensionales del universo. Ojo, no defiendo la consistencia de la teoría de cuerdas, sólo apunto que los números complejos se han desarrollado bastante desde la época de Gauss. Saludos.
Francis, estoy de acuerdo contigo y no digo nada en contrario en mi comentario anterior. Pero la ciencia es ciencia, sea o no publicada y publicitada. Una cosa es hacer ciencia y otra afirmar que la ciencia es ciencia sólo cuando se publica. Por otro lado, el hecho de que ciertos resultados se publiquen no garantiza el consenso de la comunidad, por el contrario es frecuente que conciten el rechazo y el descrédito de los que publicaron y anunciaron a los cuatro viento sus hallazgos. El británico Frederick Guthrie, que tuvo problemas con sus publicaciones en la Royal Society, fue uno de los fundadores de la Physical Society. Guthtrie blindó la sociedad a los que no fueran físicos. El consenso a veces es caprichoso y no siempre es un indicador fiable para calibrar la calidad del trabajo científico, la historia de la ciencia está llena de ejemplos.
Cuidado, Artemio, no te equivoques, la ciencia no está llena de ejemplos de ciencia hecha en contra del consenso. Hay muy pocos ejemplos y todos tenían a favor el consenso de una buena parte de la comunidad. La ciencia es una labor colectiva y comunal, y siempre lo ha sido. Quien opine lo contrario sabe como de historia de la ciencia.
Francis, no me quiero enredar en un debate que me temo resultará estéril, así que fiel a mi escepticismo saludable mantengo mis dudas confiado en que la naturaleza humana es la que es. Sólo un apunte breve; hay un episodio oscuro de la historia de la física que involucró a Newton y Robert Hookes y que tiene que ver tanto con el consenso (lo que esto signifique) y la lucha de egos. Supe del asunto por un artículo de Naukas escrito por Javier Maravall en su condición de colaborador invitado. La cosa es que Hooke le reclamó a Newton y a sus colegas científicos la autoría de la ley de la gravitación universal. Escribe Maravall:
“En 1666 Hooke exponía ante la Royal Society su trabajo sobre “La inflexión de un movimiento directo en uno curvo por la intervención de un principio activo”: el primer artículo conocido donde se explanaba el concepto de que una fuerza atractiva en el centro de un sistema planetario cambie la trayectoria rectilínea de un cuerpo a otro curvilínea; es decir, una exposición de la inercia y por consiguiente de la primera ley de Newton».
“Después de corregir un par de errores cometidos por Newton en su correspondencia, Hooke escribió un párrafo clave en su contribución a la gravitación, principal evidencia para Hooke de que fue él quien sugirió a Newton la ley cuadrático-inversa: “Mi suposición es que la atracción se halla siempre en una proporción doble a la distancia del centro recíproco, y en consecuencia que la velocidad se hallará en proporción subduplicada respecto a la atracción y por consiguiente, como supone Kepler, recíproca a la distancia.”
Lo sorprendente del caso es que a pesar de los intentos de Halley para reconocer las aportaciones de Hooke, en la primera parte de los Principia no apareció ningún agradecimiento hacia él, y la Sociedad no le respaldó en sus quejas a Newton. La naturaleza humana es la que es, y si bien el consenso está favor de Newton, los hechos muestran una perspectiva del asunto que no está clara.
https://naukas.com/2013/06/11/el-genio-olvidado-de-robert-hooke/