El fondo cósmico de microondas observado por el telescopio espacial Planck de la ESA permite estudiar la topología del universo. Nada exige que sea simplemente conexo, luego nada prohíbe que sea multiconexo. En dicho caso se observarían múltiples imágenes de una misma galaxia. Y también múltiples imágenes de las anisotropías térmicas en la radiación de fondo cósmico de microondas.
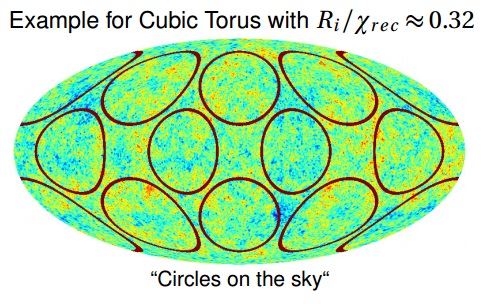
El telescopio espacial Planck no ha observado «círculos en el cielo» con lo que se descarta que el universo sea múltiplemente conexo. Nos lo cuenta Dmitry Pogosyan, «Topology of the Universe from Planck CMB,» [PDF Slides] 29 Jan 2015, Cosmology on Safari, Bonamanzi, KwaZulu-Natal, 26-30 Jan 2015 [Programme].
Por cierto, la clasificación de Thurston (teorema de geometrización) de las variedades riemannianas en tres dimensiones nos ofrece 18 tipos de espacios locamente euclídeos (17 son multiconexos y están asociadoss a los 17 grupos cristalográficos o isométricos); 10 son cerrados (compactos) y 8 son abiertos (no compactos). Más información en M. Lachieze-Rey, J.P.Luminet, «Cosmic Topology,» Physics Reports 254: 135-214, 1995, doi: 10.1016/0370-1573(94)00085-H, arXiv:gr-qc/9605010.
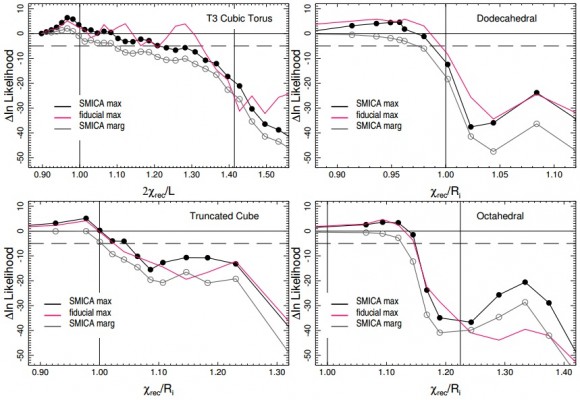
Fijando posibles topologías para el espaciotiempo se puede determinar por ordenador la señal esperada en el fondo cósmico de microondas. Dicha señal se compara con las observaciones y permite estimar la verosimilitud estadística de que dicha topología describa el universo observado.
La inferencia estadística nos permite estimar los parámetros de un modelo con máxima verosimilitud. Mediante simulaciones por ordenador por el método de Montecarlo se simulan posibles señales y se comparan sus parámetros estadísticos con la señal observada. La colaboración Planck suele usar un método de estimación fiducial (o de Fisher), que evita tener que conocer la distribución de probabilidad a priori (requisito de la estimación bayesiana). El problema es que la interpretación de los resultados fiduciales es más complicada que en el caso bayesiano (donde ayudan mucho las probabilidades condicionales).
En cualquier caso, los nuevos resultados sobre la topología del universo a partir de los análisis del telescopio Planck (sin polarización) apuntan a un universo simplemente conexo. Cuando se publiquen los mapas de polarización del fondo cósmico de microondas de Planck se podrán repetir estos análisis y confirmar de forma independiente que nuestro universo es simplemente conexo.



hola profesor Francisco
Que significa que nuestro universo sea monoconexo? significa que es plano? pero si es plano que forma tiene y fuera de el que hay? si el unverso tiene 3 dimensiones espaciales macroscopicas que hay afuera o esta dentro de una dimension mayor? y si tiene curva, significa que se curva en una 4 dimension espacial?
Ignacio, el universo es plano (según Planck su curvatura es Ωk = 0,000 ± 0,005 al 95% CL). La curvatura es un concepto de geometría intrínseca (por ejemplo la superficie de un cilindro, de un toro (dónut) o de un cono tienen curvatura cero, pues se pueden cortar y desplegar en un plano). El universo lo es todo y no existe el afuera o el adentro. Resulta difícil de imaginar pero así es.
Otra cuestión es la topología, si el universo es abierto («infinito» como un plano) o cerrado («finito» como un toro). Podría ser una especie de «cono» cuyo vértice es el falso vacío preinflacionario. No lo sabemos aún.
Lo que debes recordar es que no podemos imaginar un espaciotiempo de 4 dimensiones, o un espacio de 3 dimensiones. Vivimos en 3 dimensiones y sólo podemos imaginar superficies de 2 dimensiones. Sin embargo, desde el punto de vista matemático podemos describir cualquier (hiper)superficie en tres dimensiones sin necesidad de sumergirla en ningún espacio de dimensión superior.
Saludos
Francisco
Igual y la estoy liando al tratar de compaginar las matemáticas con la imaginación, pero si el espacio se puede representar con 3 dimensiones y la 4 dimensión es la temporal, entonces ¿podemos imaginar al universo como una esfera en continua expansión y en cuyo centro se «encuentra» el big bang? ¿o es precisamente a eso a lo que se refiere que sea multiconexo o no?
Si es monoconexo, entonces no podemos imaginarlo como una esfera, aunque se me ocurre que, dado que en el período de inflación, el espacio se expandió más rápido que la velocidad de la luz, es posible que la luz de una región no pueda darle una sola vuelta al universo, menos siendo que en la actualidad sigue expandiéndose.
Una disculpa si soy demasiado lioso, pero creo que tengo más imaginación que inteligencia matemática, y hasta eso de la imaginación es un poco dudoso.
Saludos.
Miguel Espinosa:
Respecto a la primer pregunta: No, no puedes representar al universo de esa forma.
El big bang no es «el centro» de la esfera en expansión. Estrictamente hablando el modelo FRWL no es válido cerca de la singularidad inicial pues en el «lugar» donde el factor de escala se hace cero la densidad de energía diverge (al igual que el escalar de Ricci). Pero intuitivamente el problema con la imagen del big bang como el centro de la expansión es que el big bang es la propia esfera en expansión.
Lo curioso del asunto de la topología es que es difícil descartar diversos modelos de forma observacional y aún con topología «trivial» no es fácil distinguir (que yo sepa) S^3 de RP^3 (el espacio proyectivo 3-dimensional).
Si los datos dicen que el universo es monoconexo bueno… no es cierto que la 3-esfera sea la única 3-variedad conexa (primer grupo de homología trivial) salvo homeomorfismo hay un contraejemplo hermosísimo a esta afirmación llamado «espacio de Poincaré» cuya construcción justamente señala muchas de las sutilezas de la conjetura de Poincaré
La superficie del cilindro y el cono tienen curvatura nula, pero la del toro, no (me refiero, por supuesto, a estas superficies inmersas en un espacio tridimensional euclidiano y monoconexo).
Por curiosidad, ¿al decir cono se refiere a la «trompeta de Gabriel» (me gusta más llamarlo así que «trompeta de Picard»), que también se ha sugerido para describir la topología del Universo?
Recordé las publicaciones de J-P Luminet.
Copio aquí un comentario que he visto en facebook, del cual comparto la duda:
» …que cada dos puntos estén unidos por infinidad de geodésicas. » ¿Puedes explicar un poco como sería posible esto?
Gracias.
Por ejemplo, en un toro plano todo par de puntos está unido por infinitas geodésicas (ojo, no son todas el camino más corto entre los dos puntos, sólo caminos «localmente rectos»).
¿Antonio, perdona, qué es un «toro plano»?
Albert: un toro plano es aquel que tiene curvatura nula.
¿Alguna vez has jugado a un videojuego en el que vas en una nave espacial y si llegas al borde derecho de la pantalla sales por el izquierdo y si llegas al borde superior sales por el inferior? Pues ese tipo de espacio de dos dimensiones es un toro plano.
En ese caso estoy de acuerdo, ¿pero cómo extiendes el ejemplo a una variedad con signatura de Lorentz?
Según el artículo:
Por cierto, la clasificación de Thurston (teorema de geometrización) de las variedades riemannianas en tres dimensiones nos ofrece 18 tipos de espacios locamente euclídeos (17 son multiconexos y están asociadoss a los 17 grupos cristalográficos o isométricos); 10 son cerrados (compactos) y 8 son abiertos (no compactos). Más información en M. Lachieze-Rey, J.P.Luminet, “Cosmic Topology,” Physics Reports 254: 135-214, 1995, doi: 10.1016/0370-1573(94)00085-H, arXiv:gr-qc/9605010.
A ver, no es necesario que copies y pegues un trozo del artículo, evidentemente eso ya lo he leído.
La duda iba relacionada a otra frase: ” …que cada dos puntos estén unidos por infinidad de geodésicas.” en el contexto de una variedad con signatura de Lorentz (es decir, para nuestro universo).
Pero parece que Francis ha decidido editar el post y eliminar esa parte, imagino que porque lo que la frase decía es incorrecto.
Saludos.
A eso es a lo que te respondía. De los 18 tipos de variedades, 17 son multiconexos. Luego ejemplos hay. Y si quieres ver los detalles de por qué son multiconexos, tienes el enlace al artículo técnico.
Por otra parte, veo que también ha cambiado el nombre de ‘monoconexo’ por ‘simplemente conexo’, que es una definición distinta.
No nos estamos entendiendo. Lo que has respondido, extraído del artículo, hace referencia a variedades tres dimensionales localmente euclídeas. Eso es por tanto no aplicable a una variedad cuatro dimensional localmente Lorentz.
Ah, vale. De todas formas, como el universo a gran escala es prácticamente plano, me extrañaría que no se pudieran adaptar las geodésicas de los ejemplos al caso del universo real. Otro asunto sería cómo tener en cuenta la dimensión temporal. Ahí ya no sé si se podría adaptar el ejemplo, no conozco mucho de relatividad (soy matemático, no físico).
La dimensión temporal es clave, si uno habla únicamente de las coordenadas espaciales no se refiere a geodésicas, ahí estaba el origen de la duda.
Saludos.
Albert: explican en forma didáctica qué es un toro plano (a partir de la séptima figura y lo llaman euclidean 2-torus.
Rectifico:
Albert: aquí explican en forma didáctica qué es un toro plano a partir de la séptima figura y lo llaman euclidean 2-torus.
https://www.youtube.com/watch?v=FF3FgYpBWUk&feature=youtu.be
Habría que hacerle mucho caso a este vídeo?
De ser así, esta forma de espiral logarítmica no concuerda con la investigación llevada en diciembre del año pasado de que la geometría del espacio-tiempo seguia una proporción áurea?http://www.abc.es/ciencia/20141216/abci-tambien-espacio-tiempo-esta-201412161107.html
(ya se que es del abc… pero si alguien aun así puede aclararme algo seria de ayuda)
ANONIMO, ¿sabes lo que es la línea blanca que ha sido curvada para formar una espiral? Las espirales que se ven en el vídeo son simulaciones para una cosmología Bianchi VIIh (obtenidas con el software BIANCHI2). Esta cosmología predice espirales, pero, lo siento, no tienen nada que ver con el número áureo.
El artículo citado en el vídeo es Planck Collaboration, «Planck 2013 results. XXVI. Background geometry and topology of the Universe,» arXiv:1303.5086 [astro-ph.CO]. Puedes leer en dicho artículo que los parámetros cosmológicos de la cosmología Bianchi VIIh están en desacuerdo («disagreement») con lo observado. Las espirales que aparecen en el vídeo se muestran en el artículo porque se usaron para estudiar esta cuestión.
El resultado más reciente es Planck Collaboration, «Planck 2015 results. XVIII. Background geometry & topology,» arXiv:1502.01593 [astro-ph.CO]. Va más allá y afirma que el desacuerdo con la cosmología Bianchi VIIh ahora es fuerte («strong disagreement»).
Lo siento, nuestro universo no es Bianchi VIIh.
Saludos
Francis
Saludos Dr Francis
Una consulta, una geometría del universo plana, no excluye una topología cerrada? como se dará cuenta mis conocimientos de topología son casi nulos, de ante mano gracias.
si alguien mas se anima a responderme, igualmente gracias.