
El campo de Higgs no explica la masa del protón (938 MeV/c²) y, de hecho, el protón tendría masa incluso si los quarks no tuvieran masa (que es lo que explica el campo de Higgs)(*). Mediante simulaciones por ordenador se puede repartir la masa del protón en cuatro factores. Se publica en Physical Review Letters el resultado más preciso hasta el momento. La masa de sus quarks contribuye un 9% del total, y su energía cinética y potencial da cuenta de un 32%. La energía cinética y potencial de los gluones (que unen a los quarks entre sí) contribuye un 36%. El 23% restante es debido a un cuarto de la anomalía de traza (debida a la corriente no conservada asociada a que las correcciones cuánticas no preservan la invariancia de escala de la cromodinámica cuántica (QCD) en el límite quiral). Calcular estos números es tan difícil que sus errores aún son de unos tantos por ciento.
Como ya expliqué en «La masa de un protón, la masa de sus quarks y la energía cinética de sus gluones», LCMF 30 Abr 2012, la masa del protón se reparte en cuatro términos 〈HQCD〉= 〈Hm〉+ 〈HE〉 + 〈Hg〉 + 〈Ha〉/4, donde la H significa hamiltoniano y QCD cromodinámica cuántica. El término 〈Hm〉 = 9(2)(1)% representa la contribución de la masa de todos los quarks y antiquarks del protón, incluyendo los quarks de valencia. El término 〈HE〉 = 32(4)(4)% representa la energía cinética y potencial de los quarks y antiquarks del protón. El término 〈Hg〉 = 36(5)(4)% representa la energía cinética y potencial de los gluones del protón. Finalmente, el término 〈Ha〉/4 = 23(1)(1)% representa la energía de los gluones debida a la anomalía de traza para Nf = 2 +1 sabores de quarks (es decir, teniendo en cuenta los quarks extraños en el protón).
El artículo es Yi-Bo Yang, Jian Liang, …, Zhaofeng Liu, «Proton Mass Decomposition from the QCD Energy Momentum Tensor,» Phys. Rev. Lett. 121: 212001 (19 Nov 2018), doi: 10.1103/PhysRevLett.121.212001, arXiv:1808.08677 [hep-lat]; más información en André Walker-Loud, «Viewpoint: Dissecting the Mass of the Proton,» Physics 11: 118 (19 Nov 2018) [link], y Emily Conover, «Physicists finally calculated where the proton’s mass comes from. Only 9 percent of the subatomic particle’s bulk comes from the mass of its quarks,» ScienceNews, 26 Nov 2018.
(*) [PS 29 Nov 2018] Como nos aclara Rogue Quark, @RogueQuark, «aunque los quarks de la simulación tuvieran masa cero, el protón tendría masa no nula, precisamente por los otros términos que contribuyen al hamiltoniano; los autores usan 2 + 1 sabores (tomando el u y el d como degenerados) porque emplean DWF, que es una regularización supercara computacionalmente. Con otras regularizaciones fermiónicas se simulan 2+1+1 o incluso 1+1+1+1, a valores físicos de la masa de los quarks. En cualquier caso, la contribución del charm a la masa del protón es pequeña (¡pero podría ser apreciable!). Nosotros hemos calculado el contenido de charm del nucleón, pero los errores son enormes todavía». Si no existiera el campo de Higgs, el protón tendría masa, como nos cuentan Chris Quigg, Robert Shrock, «Gedanken Worlds without Higgs: QCD-Induced Electroweak Symmetry Breaking,» Phys. Rev. D 79: 096002 (2009), doi: 10.1103/PhysRevD.79.096002, arXiv:0901.3958 [hep-ph]. [/PS]
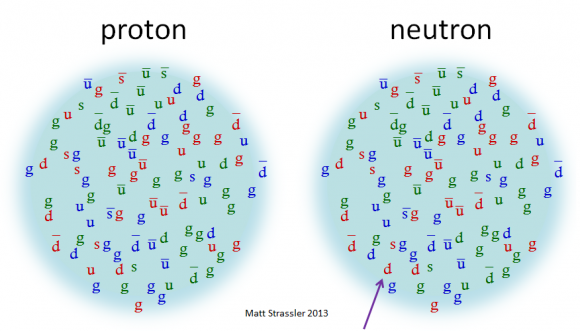
Recuerda que la suma de la masa de los quarks de valencia del protón, dos quark arriba (u) cada uno con unos 2.4 MeV/c² y un quark abajo (d) de unos 5.0 MeV/c² totalizando 9.8 MeV/c², da cuenta solo de 1% de su masa. La energía de los gluones en el protón es tan alta que se producen gran número de parejas quark-antiquark virtuales, cuya masa también contribuye a la masa del total. Por tanto, el 9% de la masa del protón debida al Higgs incluye la masa de quarks y antiquarks arriba (u), abajo (d) e, incluso, extraño (s). Por ello, las nuevas simulaciones mediante QCD en el retículo (Lattice QCD) usan un modelo de tres sabores (2+1) para los quarks en el protón.
Podemos tener una idea sencilla de la energía cinética de los quarks en el interior del protón aplicando el principio de indeterminación de Heisenberg. Como el diámetro del protón es de un femtómetro (10−15 m), su momento lineal es muy grande, resultando una energía cinética de unos 300 MeV (que da cuenta más o menos de un tercio de la masa del protón). El cálculo preciso publicado en PRL calcula un 32%, lo que indica que nuestra estimación grosera no es tan mala.

Los cálculos numéricos se han realizado en el Laboratorio Nacional Oak Ridge de EE UU (donde se encuentra Summit, que usa tecnología de IBM, el superordenador número uno en el TOP500 Nov 2018). A pesar de ello, el coste computacional es tan alto que los resultados tienen un gran error. Los futuros superordenadores en la escala de los exaflops serán imprescindibles para reducir el error en estos cálculos, fundamentales para muchos tests de precisión del modelo estándar (p. ej. la futura determinación de la masa de los neutrinos). Por ello hay que seguir trabajando para reducir los errores aún más.


Hola Francis,
Muy interesante articulo. Hablando de neutrinos, que opinas sobre este resultado de MiniBoone
A. A. Aguilar-Arevalo et al. (MiniBooNE Collaboration), “Significant excess of electronlike events in the MiniBooNE short-baseline neutrino experiment,” Phys. Rev. Lett. 121, 221801 (2018).
Un saludo
Javier, puedes leer «MiniBooNE y LSND observan un exceso a 6.1 sigmas cuyo origen apunta a neutrinos estériles», LCMF, 01 Jun 2018.
¿La anomalía de traza tiene que ver con que el campo gluón interactúe consigo mismo?
Paco:
Habrías de ser más explícito porque la pregunta es sutil, pero en principio no tiene que ver una cosa con la otra. Podrías tener una teoría Yang-Mills SU(N) con N>1 con lagrangiano L = (1/g^2)Tr[F] (donde F es el tensor de campo) pura en la que los gluones autointeractuan y libre de anomalía de traza, en este caso en particular la traza del tensor de energía momento T va como Tr(T) = β(g)Tr[F^2] y es cero porque Tr[F^2]=0, si añadís términos cinéticos para fermiones quirales en el lagrangiano Tr(T) no será cero y de hecho será proporcional a la corrección a un lazo (fermiónico) a la función beta. Los «culpables» de la no anulación de la anomalía de traza son los fermiones quirales (quarks) que se acoplan a los gluones
Lo fascinante del asunto es si se introducen n(>>1) sabores de quarks no quirales el lagrangiano clásico tendrá simetría global SU(n)xSU(n) (y un U(1) extra de número bariónico) pero al cuantizar ocurre que efectos no perturbativos del vacío de QCD producen el rompimiento de simetría SU(n) x SU(n) —> SU(n) y el tensor de energía momento adquiere un valor de expectación a la manera que describí en el primer párrafo.
Saludos.
Gracias por la respuesta.
Pero me temo que aunque llego a bastantes cosas para ser un playmóbil (lego), a tanto creo que no llego xD
Quiero entender de tu explicación (precaución: posible estupidez incoming) que la anomalía que al igual que con los electrones que son levógiros y dextrógiros y sólo uno de ellos interacciona con los fotones, a los quarks les pasa lo mismo con los gluones. Y eso tiene como consecuencia la anomalía.
Del segundo párrafo no consigo sacar demasiado, lo siento 🙁
Es que he estado buscando y no encuentro explicación, aunque sea algo inexacta, a la anomalía de traza. Me refiero a una explicación que no consista en un desarrollo matemático. Me valdría en inglés también.
Aunque soy plenamente consciente de que puede no existir esa explicación sin matemáticas o puede ser una mierda de explicación xD.
Gracias también por escribir, tus comentarios son siempre muy interesantes, aunque yo que leo mucho entradas antiguas, me da la sensación de que antes escribías más.
Paco:
Una disculpa no pretendía ser pedante. Es difícil explicar lo que es una anomalía sin matemáticas, es aún más difícil explicar la anomalía de traza porque su origen no es entendido hasta la fecha, nadie en el mundo os podrá contar su explicación profunda, es uno de los problemas gigantes en la física teórica 🙂 y por ello es tan emocionante como la física de frontera 🙂
La anomalía de traza tiene relación con confinamiento en gluones, a modo muy burdo se puede decir que el hecho de que no podamos hacer un experimento para detectar una carga de color aislada es equivalente a que que las excitaciones mas relevantes del vacío serán las siguientes:
1) un par de fermiones unidos por una «cadena de gluones» o líneas de flujo del campo de color ( cuerda abierta 😉 )
2) una línea cerrada de gluones (cuerda cerrada ;D )
Podeís reflexionar y notar que ambos estados son compatibles con el hecho de que es imposible observar cargas de color libres. La animación en wikipedia de estas cuerdas y como «se rompen» de manera que no se observen cargas de color es muy ilustrativa https://en.wikipedia.org/wiki/Color_confinement. Ahora bien, la cuerda abierta tiene una «longitud característica», mi analogía para explicar la anomalía de traza es que esa longitud rompe la invarianza ante escala de la teoría clásica, la teoría cuántica ya no es invariante ante cambios de escala porque si hay confinamiento habrá una escala característica.
Cuando las simetrías se rompen, aparecen bosones de Goldstone o goldstinos, las «cuerdas abiertas» mencionadas deben su existencia a esta rotura de la simetría de escala, estas cuerdas serán los bosones de Goldstone que indican que se rompió la simetría mencionada, este es el origen del octeto de mesones en QCD, los mesones son los bosones de Goldstone. Burdamente eso es la anomalía de traza.
Precauciones:
-Decir que sólo esas dos excitaciones son «relevantes» es una simplificación, un mesón no es un par de quarks así como un hadrón no es un trío de de ellos , un artículo de Francis al respecto https://francisthemulenews.wordpress.com/2012/04/30/la-masa-de-un-proton-la-masa-de-sus-quarks-y-la-energia-cinetica-de-sus-gluones/
-Decir que «la anomalía de traza es un fallo en ser invariante ante escala» también es simplificar bastante pero me parece que muy razonable, después de todo en una teoría de norma pura el valor de expectación de la traza del tensor de energía momento es la masa del bosón de norma, pero en caso de que quieras profundizar está discusión viene bien: https://physics.stackexchange.com/questions/70823/the-phrase-trace-anomaly-seems-to-be-used-in-two-different-ways-whats-the-re/70827
Lo mencionado es una consecuencia de la anomalía de traza y no explica cual es su origen. El origen de esta debe ser un efecto del vacío QCD y entenderlo es uno de los problemas más vitales de la física contemporánea. Posiblemente analogías con materia condensada puedan ayudarte a profundizar:
https://en.wikipedia.org/wiki/Fermionic_condensate
Este artículo es muy provocativo: https://francis.naukas.com/2016/10/25/semimetales-de-weyl-arcos-de-fermi-y-anomalias-quirales/
Te comparto un artículo divulgativo clásico sobre confinamiento.
Black Holes and Confinement, Edward Witten.
https://www.sns.ias.edu/ckfinder/userfiles/files/CurrentScienceVol81(4).pdf
Saludos!
Por cierto: Las componentes derechas e izquierdas del campo del electrón se acoplan al campo del fotón, no es verdad que una si lo haga y la otra no (y similarmente con quarks y gluones).
Hay que tener mucho cuidado con los nombres, se le llama «límite quiral» a cuando se asume que la masa de los quarks es cero, en ese caso el lagrangiano tendrá simetría global SU(n) x SU(n) y los generadores de la simetría de cada factor de ese producto actuan sobre las componentes izquierdas y derechas respectivamente y cuando se rompe esa simetría (a la manera que describí en mi primer comentario) la teoría se vuelve «quiral «https://en.wikipedia.org/wiki/Chiral_symmetry_breaking pero no debes pensar que una componente deja de acoplarse a los gluones y la otra no.
Muchísimas gracias.
He tardado en responder porque éste tipo de cosas hay que pillarlas con ganas y despejado para que exista alguna mínima posibilidad de que entienda algo xD
La verdad es que me ha ayudado mucho lo que me has comentado de la anomalía de traza.
Pero éste último mensaje me ha dejado un poco el culo torcido con lo de los electrones. ¿Qué era entonces lo que ocurría distinto con los electrones levógiros y dextrógiros en el campo electromagnético? Me suena que algo pasaba diferente…
La verdad es que estaría horas preguntándote cosas. Y si es con un par de birras delante ni te cuento xD
los quarks de valencia representan los estables de un hadrón ?
Gael:
Los quarks de valencia de un hadrón no son estables, este post de Francis es muy ilustrativo al respecto de lo que preguntas: https://francisthemulenews.wordpress.com/2012/04/30/la-masa-de-un-proton-la-masa-de-sus-quarks-y-la-energia-cinetica-de-sus-gluones/
También me permito recomendar este otro:
https://francis.naukas.com/2013/11/19/la-masa-de-los-tres-quarks-mas-ligeros/