
La superconductividad en el grafeno bicapa rotado con ángulo mágico (MATBG) fue la gran sorpresa de 2018 en Física. Para un ángulo «mágico» θ = 1.1º ± 0.1º se alcanzó una temperatura crítica (Tc) de 1.7 kelvin. ¿Cómo influye en la Tc la uniformidad en el ángulo de rotación? Se publica en arXiv una Tc = ~3 K para un dispositivo MATBG con un ángulo θ = 1.10º ± 0.01º (diez veces más uniforme en ángulo). Se observan nuevos domos superconductores y nuevos estados aislantes entre ellos. Más aún, aparecen estados topológicos con número de Chern no nulo. No se conoce la teoría que explique todos estos fenómenos, pero parece claro que hay que explorar dispositivos con un ángulo extremadamente uniforme para ayudar a descubrirla.
Te recuerdo que el descubrimiento fue obra del grupo del físico español Pablo Jarillo-Herrero (MIT, EE UU). Publicado en Nature, ha sido citado más de 600 veces en un solo un año y el número de citas sigue creciendo a diario. El grafeno bicapa rotado con ángulos pequeños se comporta como un dispositivo de moiré con una estructura de bandas muy plana; por ello, los portadores de carga están muy localizados en la red de moiré (puntos AA), se mueven a baja velocidad y están fuertemente correlacionados a gran distancia. Las bandas asociadas a cada celda de moiré presentan nueve posibles estados de llenado con un número entero de «electrones» (ν = +1, +2, +3, o +4) y «huecos» (ν = −4, −3, −2, o −1), además del estado neutro (ν = 0). El año pasado se observaron domos superconductores alrededor de los estados semillenos ν = −2, y +2, que eran aislantes. El nuevo artículo observa estados aislantes para todos los números enteros de llenado (ν = 0, ±1, ±2 y ±3), así como tres nuevos domos superconductores alrededor de ν = −1, 0, y +1, con Tc = 0.14, 0.16, y 0.65 K (además del domo cerca de ν = −2 con Tc = 3 K).
La teoría que explique estas observaciones, que promete ayudar a desvelar el secreto de los superconductores de alta temperatura, requiere más estudio experimental de dispositivos grandes (para evitar los posibles efectos de borde) fabricados con una calidad extrema (que eviten cambios en el ángulo conformen se propaguen los portadores). Acabarán siendo fabricados y estudiados. Mientras tanto, los teóricos seguirán proponiendo nuevas ideas. La «twistrónica» es uno de los campos más fascinantes de la física de la materia condensada y lo seguirá siendo por mucho tiempo. El nuevo artículo (que auguro que acabará publicado en Nature) es Xiaobo Lu, …, Allan H. MacDonald, Dmitri K. Efetov, «Superconductors, Orbital Magnets, and Correlated States in Magic Angle Bilayer Graphene,» arXiv:1903.06513 [cond-mat.str-el] (15 Mar 2019); más información en Allan H. MacDonald, «Bilayer Graphene’s Wicked, Twisted Road,» APS Physics 12: 12 (06 May 2019) [link]. Por cierto, el autor que lidera este artículo, Efetov, está afincado en España, en el ICFO (Institut de Ciencies Fotoniques, Barcelona, España).
[PS 30 oct 2019] El artículo se ha publicado en Nature como auguré: Xiaobo Lu, Petr Stepanov, …, Dmitri K. Efetov, «Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene,» Nature 574: 653-657 (30 Oct 2019), doi: https://doi.org/10.1038/s41586-019-1695-0, arXiv:1903.06513 [cond-mat.str-el] (15 Mar 2019). [/PS]

Fabricar dispositivos de grafeno parece trivial, pero es muy difícil (todo un arte manual). En el nuevo artículo solo se han fabricado y caracterizado dos dispositivos (D1 con θ = 1.10º ± 0.01º, y D2 con θ = 1.08º ± 0.01º). La gran maravilla del grafeno bicapa rotado (tBLG) es que se puede dopar con electrones y huecos de forma eléctrica (basta «enchufarlo» a una corriente eléctrica con la polaridad deseada); además, para controlar el nivel de dopado solo hay que cambiar la corriente eléctrica aplicada (más fácil imposible). Por contra, los cupratos y otros superconductores de alta temperatura requieren la síntesis química con un nivel controlado de dopantes; por tanto, para estudiar diez niveles de dopado hay que sintetizar diez materiales con diferente dopado (en el tBLG basta aplicar diez corrientes eléctricas sobre el mismo dispositivo). De hecho, para dopar un cuprato con electrones (huecos) hay que sintetizarlo con un átomo dador (aceptor) de electrones adecuado; por ejemplo, Ba1−xKxFe2As2 para huecos y Ba(Fe1−xCox)2As2 para electrones, siendo 0<x<1 el nivel de dopado.
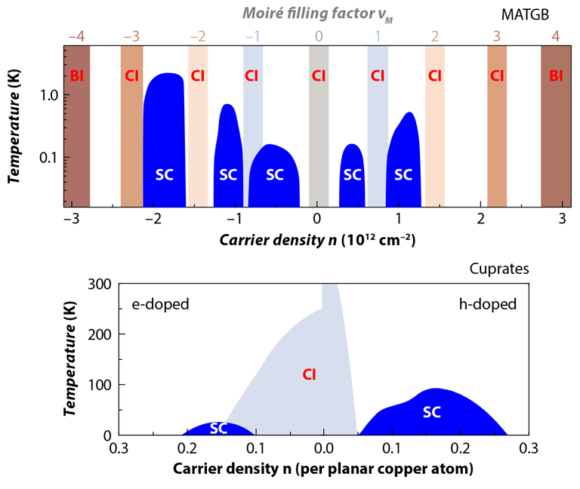
La superconductividad en el grafeno bicapa rotado con ángulo mágico (MATBG) tiene el récord de densidad de carga (en el nuevo artículo para el domo entre ν = −1 y ν = 0 se observa para n ~ 3 × 1011 cm-2). La correlación entre los portadores (electrones o huecos según el dopado) es tan fuerte, que aunque estén separados una gran distancia (la constante de red de la estructura de moiré del MATBG, que es unas cien veces mayor que distancia entre átomos de carbono en el grafeno) que aparecen estados aislantes (que podrían ser de tipo Mott, aunque aún no está confirmado) para todos los niveles de llenado (para ν entero).

Por cierto, Allan H. MacDonald (Univ. Texas), que acuñó en 2011 el término «ángulo mágico» (porque no tenía explicación para su origen), es uno de los autores del nuevo artículo. Lo destaco porque ya predijo que habría estados aislantes para cada nivel de llenado y domos superconductores entre ellos en el MATBG. Lo hizo en enero de 2019 en su charla inaugural de la conferencia «Correlations in Moire Flat Bands» (KITP, online talks). Aquí está el dibujo que presentó, que como es obvio es muy aproximado; MacDonald confesó que es así porque se limitó a usar el copy & paste en Paint. ¿Por qué realizó esta predicción? Porque la correlación entre los electrones es muy fuerte; si era tan fuerte para producir aislantes Mott para los estados semillenos, no había ninguna razón para que no fuera tan fuerte como para producirlos para todos los niveles enteros de llenado, incluido el punto neutro. Te recomiendo disfrutar su charla [video] donde nos muestra su gran intuición.
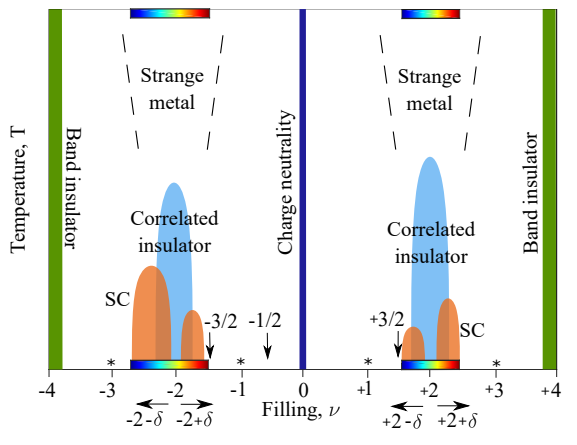
Quizás puedas pensar ahora, que se ha confirmado la intuición de MacDonald, que su predicción era obvia. Pero no es así, como puedes ver en este diagrama de Jarillo-Herrero de enero de 2019, donde solo se muestran en los niveles semillenos los estados aislantes (que ahora se llaman «aislantes correlacionados» porque hay dudas de que sean aislantes Mott como se creía). Los asteriscos apuntan a que pasa algo en los otros niveles de llenado enteros, pero Jarillo-Herrero y sus colegas no se atreven a afirmar la osadía de MacDonald (que también deben ser estados aislantes correlacionados). Por cierto, esta figura está extraída del recomendable artículo Yuan Cao, Debanjan Chowdhury, …, Pablo Jarillo-Herrero, «Strange metal in magic-angle graphene with near Planckian dissipation,» arXiv:1901.03710 [cond-mat.str-el] (11 Jan 2019); en este artículo se muestra que la resistencia lineal predicha por ideas de teoría de cuerdas (dualidad holográfica en materia condensada), que comenté al final en mi charla sobre la historia de la teoría de cuerdas en Desgranando Ciencia 2018 [youtube], no explica bien las observaciones en el MATBG.

Recuerda que las bandas corresponden a la relación entre momento lineal (producto de velocidad y masa) y energía (cinética). La pendiente de las bandas determina la velocidad de los portadores y su curvatura determina su masa efectiva. Para bandas planas en el MATBG los portadores tienen un momento muy pequeño y una masa efectiva grande. Por contra, en el grafeno monocapa el momento es máximo (la velocidad es la máxima posible, llamada velocidad de Fermi) y su masa es mínima (las bandas son lineales, llamados conos de Dirac); por ello, en el grafeno monocapa se propagan cuasipartículas de tipo fermión de Dirac sin masa.

Volviendo al nuevo artículo, esta figura muestra una ampliación de los nuevos domos superconductores observados alrededor de los niveles de llenado ν = −1, 0, y +1. La tabla muestra sus temperaturas críticas Tc (todas ellas por debajo de 1 K, en las tres últimas filas de la tabla), así como su campo magnético crítico y su longitud de coherencia de Ginzburg–Landau. Como estos estados superconductores no fueron observados en el artículo de Jarillo-Herrero, ni en otros artículos que replicaron su resultado más tarde, todo indica que la clave de su observación es la calidad de fabricación del dispositivo (el ángulo debe ser muy uniforme en toda el área de contacto de las dos hojas de grafeno).

En mi opinión lo más sorprendente del nuevo artículo es la observación de estados topológicos con un número de Chern no nulo al aplicar un campo magnético transversal. Para una temperatura de 100 mK, como muestra esta figura, se observan «abanicos» de Landau (Landau fans) que parten del punto de neutralidad (ν = 0), así como de algunos niveles de llenado (ν = −3, −2, y +2). Se cree que, en un dispositivo aún más uniforme en ángulo, deberían aparecer en todos los niveles enteros de llenado. Para ν = −1 la resistencia no tiene pendiente dn/dB para campos magnéticos pequeños, pero por encima de un campo crítico Bc┴ ~ 3.6 T aparece una pendiente que sugiere un número de Chern igual a la unidad. También aparece para ν = +1 pero con un pendiente mayor que sugiere un número de Chern de dos. Que haya estados correlacionados topológicos conecta la superconductividad en el MATBG con la de los superconductores topológicos.

El comportamiento topológico se confirma con la observación de histéresis en la resistencia eléctrica en función del campo magnético aplicado. Aquí se muestra el caso ν = −1 para campo magnético creciente (línea sólida) y decreciente (línea discontinua) para temperaturas inferiores a 800 mK; se observa que para T > 800 mK la histéresis casi desaparece. Se interpreta este comportamiento como resultado de la competición entre los estados con número de Chern nulo y no nulo. Todo esto sugiere (aunque se necesitan estudios experimentales específicos para confirmarlo) que los pares de Cooper se podrían propagar por los bordes del dispositivo de grafeno bicapa rotado, comportándose el MATBG como un aislante en el área de la región interior del dispositivo. Sin lugar a dudas una hipótesis muy sugerente.
En resumen, confieso que he leído cientos de artículos sobre grafeno bicapa rotado en el último año y podría haberme hecho eco de muchos de ellos. Sin embargo, pocos me han llamado tanto la atención como el que destaco en esta pieza. Se han publicado muchas teorías para explicar lo observado en el MATBG, pero nuestras herramientas matemáticas aún son torpes para lidiar con sistemas de electrones fuertemente correlacionados (incluso en modelos tan sencillos como el de Hubbard). Se está avanzando, pero, como siempre, más rápido en las observaciones experimentales y computacionales (algunas parcialmente contradictorias entre sí) que en las explicaciones teóricas. Habrá que estar al loro de estos avances.


Confieso que no entiendo ni papa, tampoco me he leído el artículo entero, no podría aunque me esforzara. Pero lo que quiero destacar es la figura óptica que forma esas dos láminas de grafeno hexagonales de la segunda figura del artículo, superpuestas en ese determinado ángulo forman hexágonos más grandes y eso es lo que me parece alucinante, que las láminas formadas por hexágonos pequeños y colocadas en un cierto ángulo den la misma figura geométrica más grande y repetida.
Eso si, de las propiedades conductoras y del porqué de ellas, al formar dicha estructura geométrica colocadas de esa forma…ni papa.
Yo también he notado ese efecto óptico que se produce en muchos patrones moiré. Por ejemplo si se superponen dos mallas con orificios y se rota una con respecto a la otra se observa un patrón de interferencia que reproduce la geometría del orificio. En el caso de celdas exagonales el angulo de rotación funciona como una especie de ampliador reproduciendo la forma exagonal cada vez más grande. Muchas veces me pregunté si tal efecto no tendría algún tipo de aplicación en miscroscopía. No se si Francis sabrá si este fenómeno tiene algún nombre o se ha estudiado.