
En el efecto túnel cuántico una partícula atraviesa una barrera de energía potencial mayor que su energía cinética (algo prohibido en física clásica). Se llama duración de tunelado al tiempo que pasa la partícula «dentro» de la barrera; su medida experimental depende de cómo definamos «dentro». Se publica en Nature una nueva medida usando un condensado de Bose–Einstein (BEC) de unos 8000 átomos de rubidio que atraviesa una barrera óptica de 1.3 micrómetros en 0.61(7) milisegundos, es decir, a una velocidad de 2.1 mm/s (un proceso lento hasta el extremo, pues si el «tunelado» hubiera sido superlumínico hubiera durado menos de 4.3 femtosegundos).
Para medir una duración se requiere un reloj; se ha usado un reloj de Larmor. Cuando un conjunto de partículas de espín 1/2 incide contra una barrera en la que hay un campo magnético dichas partículas rotarán mientras se encuentren dentro de la barrera y saldrán de ella con sus espines rotados; el ángulo de rotación θ = ωLτ, donde ωL es la frecuencia de Larmor, determinará la duración del paso a través de la barrera. En el nuevo experimento se usa un BEC enfriado a 2(1) nK para que su longitud de onda de De Broglie λdB = 4(1) μm sea mayor que la anchura de la barrera óptica, cuya temperatura equivalente es de 135(8) nK. El ángulo de Larmor al otro lado de la barrera se estima con una medida de tipo Stern–Gerlach en función de la velocidad de incidencia del condensado.
Un resultado que quizás sorprenda a algunos que pensaban que el tunelado era instantáneo (o al menos superlumínico). Pero hay que recordar en la luz en los BEC se mueve ultralenta y, al revés, un BEC en una trampa óptica se mueve ultralento. El artículo es Ramón Ramos, David Spierings, …, Aephraim M. Steinberg, «Measurement of the time spent by a tunnelling atom within the barrier region,» Nature 583: 529-532 (22 Jul 2020), doi: https://doi.org/10.1038/s41586-020-2490-7, arXiv:1907.13523 [physics.atom-ph] (31 Jul 2019). Más información divulgativa en Anil Ananthaswamy, «Quantum Tunneling Is Not Instantaneous, Physicists Show,» Scientific American, 22 Jul 2020.

El paquete de ondas que describe una partícula que incide contra una barrera de potencial en parte se refleja y en parte se transmite. La parte transmitida se comporta como una onda evanescente, luego según la fórmula de Büttiker y Landauer el tiempo semiclásico estimado para el efecto túnel es de m d/(ħ κ), donde m es la masa de la partícula, d es la anchura de la barrera, (ħ κ)² = 2 m (V0−E), E es la energía de la partícula incidente, V0 es la altura de la barrera de potencial y ħ es la constante de Planck (reducida). El gran problema de verificar esta fórmula es decidir cuándo el paquete de ondas transmitido ha logrado completar el tunelado.
La idea del nuevo artículo es usar un reloj que solo haga tic-tac cuando el paquete está dentro de la barrera. Por ello se usa un reloj de Larmor y una barrera de potencial óptica cuya resolución espacial está limitada por la longitud de onda de la luz láser usada. Para que la medida sea precisa se escala el sistema para que el tiempo de Büttiker y Landauer sea del orden de los milisegundos. Para ello se usa un BEC cuya energía cinética es del orden de E ≈ 100 feV (kB × 1 nK, donde kB es la constante de Boltzmann).
Como espín para los átomos del BEC se usa el pseudoespín asociado a dos estados electrónicos hiperfinos |F = 2, mF = 2⟩ del nivel 5S½ de dichos átomos. Los dos estados de pseudoespín son |2, 0⟩, estado |+x⟩, y 2, −1⟩, estado |−x⟩, que están separados por una transición hiperfina de 6.8 GHz. Los átomos del BEC se reflejarán o se transmitirán a través de la barrera con su espín es un estado de superposición cuántica de los estados |+x⟩ y |−x⟩.
Como se observa en la figura de arriba, mientras el BEC esté dentro de la barrera, se produce una rotación del espín en la esfera de Bloch caracterizada por dos ángulos θy y θz. Así, se determinan dos tiempos de Larmor independientes τy = θy/ωL y τz = θz/ωL.
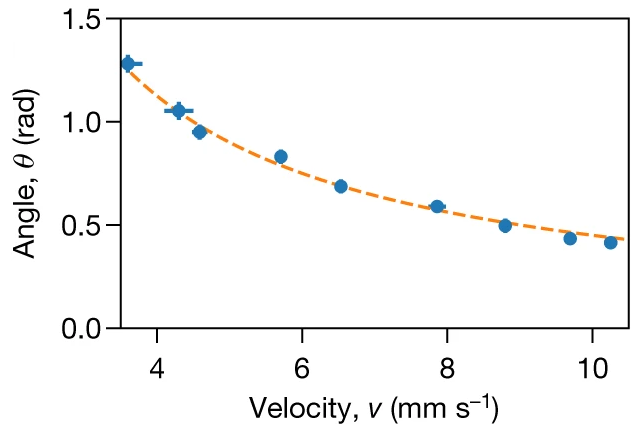
La medida del ángulo de precesión se ajusta bastante bien a la predicción teórica. La curva a trazos naranjas corresponde a la expresión Ω d/v, donde d es la anchura efectiva de la barrera, v es la velocidad incidente de los átomos y Ω es la frecuencia de Rabi, que en esta figura se estima en Ω = 2π × 440(10) Hz (esta frecuencia se puede controlar de forma independiente a la altura de la barrera). Para una barrera de 135(8) nK, que corresponde a una velocidad de 5.1 mm/s, la frecuencia de Rabi es de Ω = 2π × 225(40) Hz.

Esta figura ilustra la duración del tunelado (tiempo que pasa el BEC dentro de la barrera de potencial) en función de la velocidad de incidencia; los datos en naranja para τy y los datos en azul para τz. Para la velocidad de incidencia más baja, 4.1 mm/s, la probabilidad de transmisión es del 3 %. Dado que la probabilidad de transmisión depende de la energía, se toma como estimación de la duración del tunelado el tiempo máximo, max (τy , τz) que se observa para una velocidad de 4.8 mm/s y corresponde a κ d ≈ 3, siendo el resultado τy = 0.61(7) ms. Un resultado está en buen acuerdo con las predicciones de la ecuación de Schrödinger para el BEC (llamada ecuación de Gross–Pitaevskii). Nótese que esta duración semiclásica está en desacuerdo con τz en más de tres sigmas.
En resumen, según los autores se ha logrado la primera medida directa de la duración del efecto túnel usando partículas con masa (lo discutible está en el adjetivo «directa» pues en medidas previas también se afirmó que eran medidas directas). Lo más relevante (que sirve para justificar la publicación de este resultado en Nature) es que se descarta que el efecto túnel sea instantáneo (o superlumínico). Algo que interesará a los aficionados a las interpretaciones de la mecánica cuántica.


Yo entendía que el efecto túnel no era un paso tal cual de la partícula a través de la barrera, si no que simplemente forzaba el experimentador una probabilidad de que se pudiera medir/encontrar al otro lado al acorralarla (forzada a mostrar momento y posición a la vez)…pero leo que se encuentra durante un tiempo dentro de la barrera…confuso.
Pedro:
Uno de los postulados de la mecánica cuántica estipula que los resultados de los experimentos se calculan como autovalores de operadores hermíticos. En particular, recuerde que en mecánica cuántica no-relativista el tiempo no es un operador. De esto se sigue que la pregunta ¿Cuánto dura el efecto túnel? estrictamente hablando, no tiene sentido. Sólo tiene sentido asignar una magnitud de tiempo a un proceso que está bien aproximado por la física clásica; este no es el caso para un fenómeno «puramente cuántico» como lo es el efecto túnel.
¿Qué es entonces el tiempo medido en los experimentos que nos comunica Francis con esta entrada? Respuesta: Una construcción semi-clásica. Puede leer más información en: https://francis.naukas.com/2019/03/27/la-duracion-del-efecto-tunel-cuantico-es-imposible-de-observar/
Resolviendo su pregunta: El experimento produce un marco teórico semi-clásico para analizar un experimento tipo «túnel cuántico». En este marco, muy particular, tiene sentido asignar valores de tiempo a un proceso. Pero, estrictamente hablando, la partícula no «pasa un tiempo en la barrera». Además note que aún en esta aproximación, los resultados de las medidas siguen siendo de de naturaleza estadística, el valor de tiempo encontrado para un evento en particular, tampoco tiene sentido (de lo contrario sería física clásica y no semi-clásica); lo que tiene sentido es un valor promedio para una serie de experimentos realizados bajo las mismas condiciones experimentales.
Si el intervalo temporal que dura el efecto túnel es un sin sentido en mecánica cuántica, ¿Por qué es importante el experimento en cuestión? Porque demuestra que aún en la aproximación semi-clásica (noción también ambigua) en dónde el concepto de tiempo tiene sentido, el proceso de tunelaje no ocurre a velocidades superlumínicas. Se sigue que, para este experimento, sus suposiciones y su ventana de toma de datos, no existe un proceso físico instantáneo. Por ello es interesante.
Un saludo Pedro.
Gracias Ramiro por el apunte y por supuesto a Francis por todas las entradas.
Fue un placer, Jose Juan. En todo caso, si alguien tiene la misma duda que Pedro, lo más recomendable es ir al enlace que adjunto, allí podéis leer mi apunte elaborado con mucha más claridad y destreza por Francis.
La información es muy interesante sería bueno que incluya aplicaciones y videos relacionados con los usos de la fibra óptica
Gracias Ramiro. Como siempre genial tu explicación. 👏
Cuando hablas de la radiación de hawking se puede explicar por efecto tunel o por desintegración de particula-antipartícula, ¿no tendrá un analogo inverso para esto? o sea digo, ¿cuando hablamos de reflexión-transmisión no hablamos de efecto tunel y cuando hablamos de efecto tunel no hablamos de transmisión-reflexión ?
Otra pregunta…la imagen de la entrada parece fabulosa, pero creo que se hicieron muchisimos intentos para obtenerla…osea, no es que el condensado antes de la barrera que estamos viendo sea el mismo después…por colapso de la medida me refiero…Gracias
No sé si te entiendo bien, Hector04. Pero si estás preguntando si es posible explicar los resultados de los experimentos a los que alude esta entrada con una imagen de creación de pares, la respuesta es no. El concepto de anti-partícula surge en mecánica cuántica relativista.
Mira los números y las fórmulas del artículo. Todo se puede entender perfectamente en el contexto de la mecánica no-relativista.
Le recomiendo un video divulgativo: https://www.youtube.com/watch?v=hYkaahzFWfo
Si está interesado en el efecto túnel a velocidades relativistas (y su relación con la «creación de pares») le recomiendo «History and Physics of the Klein Paradox» https://arxiv.org/abs/quant-ph/9905076
Un saludo.
Magnífico artículo. Enhorabuena. Y, por supuesto, extensiva a los autores de la investigación. Ese intervalo de tiempo siempre ha sido un tema de discusión entre especialistas. Usar experimentalmente un condensado BE y la frecuencia Larmor es genial. O al menos a mí no se me habría ocurrido. Saludos
Recomiendo un video bastante claro y preciso sobre el tema de «la duración del efecto túnel cuántico»:
Is Quantum Tunneling Faster than Light? https://www.youtube.com/watch?v=-IfmgyXs7z8
Te felicito por divulgar física pero no es accesible para mí el nivel en que tratan. He estudiado física para a la carrera de ing. mecánica pero no llego a ese nivel. Felizmente hay libros de divulgación como por ejemplo los publicados por lo menos en España, «Un paseo por el cosmos – RBA»
Alguna vez quise estudiar física pero se truncaron mis estudios y no terminé ni la ing. mecánica.
Puedo entender la física clásica porque tiene mucho de lógica, intuición, sin mucha o ninguna contradicción con los sentidos. Pero la física de partículas es una locura. No sé por qué te cuento esto pero nuevamente te felicito.
Pepe, del Perú.
José, yo tengo la colección completa de «Un paseo por el cosmos» en casa; algunos son mejores que otros, pero en promedio están muy bien. En este blog reseñé algunos de ellos: https://francis.naukas.com/?s=un+paseo+por+el+cosmos
Un articulo hermoso aun con escasas luces bastaron unas pinceladas para poder tener un poco más de claridad sobre este campo maravilloso de la ciencia, se agradece.
Podrían dar una explicación sobre cuál es el interés, las implicaciones, con respecto a las interpretaciones de la mecánica cuántica? gracias