La fórmula de Einstein (1915) para la anomalía en el avance del perihelio de los planetas fue obtenida por primera vez en 1898 gracias a la teoría de la gravedad desarrollada por un desconocido físico alemán, maestro de escuela, llamado Paul Gerber. Su teoría suponía que la gravedad se propagaba a la velocidad de la luz y que la fuerza entre dos masas debía ser corregida por un término que dependía de la velocidad a la que se movieran. La fórmula de Gerber-Einstein explica la anomalía de Mercurio, de los planetas rocosos del Sistema Solar e incluso de la Luna (cuando se corrigen efectos adicionales debido al resto de los planetas y cuerpos del sistema solar). El trabajo de Gerber tuvo poca repercusión porque su derivación era bastante poco clara y años más tarde se descubrió que contenía errores argumentales. Einstein siempre afirmó que en 1915 desconocía el trabajo de Gerber y que incluso si lo hubiera conocido no habría influido en el desarrollo de su teoría general de la relatividad. Los grandes descubrimientos de la Historia de la Ciencia siempre tienen una historia muy intrincada y no es raro encontrar ejemplos en los que un desconocido se adelantó a un gran genio en un asunto puntual pero clave. Sobre la teoría de Gerber recomiendo el artículo del físico español Jaume Giné (Universitat de Lleida, España), «On the origin of the anomalous precession of Mercury’s perihelion,» Chaos, Solitons and Fractals 38: 1004–1010, 2008 [gratis en ArXiv] (del que he extraído las figuras con las fórmulas de esta entrada). Para la historia de la anomalía y sus modelos seguiré la descripción de N.T. Roseveare, «Leverrier to Einstein: A review of the Mercury problem,» Vistas in Astronomy 23: 165-171, 1979. Más información en John Earman and Michael Janssen, «Einstein’s Explanation of the Motion of Mercury’s Perihelion,» The Attraction of Gravitation, edited by J. Earman, M. Janssen, J.D. Norton, El trabajo de Gerber ha sido utilizado en contra de Einstein por muchos de sus detractores, como Christopher Jon Bjerknes, «The Manufacture and Sale of Saint Einstein,» chapter 12, 2006.
El astrónomo y matemático fránces Le Verrier, codescubridor de Neptuno en 1846, fue el descubridor de la anomalía en el avance del perihelio de Mercurio, una anomalía de solo 38″ (segundos de arco) por siglo (según Le Verrier). Ya en 1849 había descubierto la anomalía pero no la anunció hasta 1859, junto con una explicación, la existencia de un cinturón o anillo de materia entre el Sol y Mercurio, parecido al cinturón de asteroides entre Marte y Júpiter. Ese mismo año un astrónomo amateur llamado Leecarbault afirmó que llevaba tiempo observando un planeta pequeño en transitó por el Sol al que llamó Vulcano. La Real Sociedad Astronómica de Londres anunció a bombo y platillo que Vulcano era la explicación correcta de la anomalía del francés Le Verrier. Otros astrónomos, como el francés Babinet, el danés Buys-Ballot y el americano Kirkwood también observaron la anomalía de Le Verrier y confirmaron que el planeta Vulcano daba cuenta de ella. Más aún, múltiples astrónomos amateurs y profesionales realizaron observaciones de Vulcano (casi seguro que observaron manchas solares). En 1876 Le Verrier explicó por qué era difícil observar Vulcano y predijo sus siguientes tránsitos. Todas sus predicciones fallaron. Vulcano no existía. Le Verrier murió en 1877 sin saberlo. Vulcano tuvo sus momentos de gloria en el s. XIX pero llegó a aparecer solo en unos pocos libros de texto sobre astronomía.
Tras la muerte de Le Verrier, la anomalía en el avance del perihelio de Mercurio fue confirmada por el astrónomo norteamericano Simon Newcomb que en 1882 encontró una anomalía algo mayor, 43″ por siglo (que hoy es el valor correcto). Newcomb discutió diferentes causas posibles. Descartó que un planeta (Vulcano) o un cinturó de materia fueran la causa, no habían sido observados. También descartó que el achatamiento del Sol pudiera ser la causa. En 1894 el astrónomo Asaph Hall propuso alterar la ley de gravitación universal de Newton, la ley de la inversa del cuadrado de la distancia, añadiendo un término inverso del cubo de la distancia multiplicado por una constante que ajustó para que diera cuenta de la anomalía observada en Mercurio. En 1895 Newcomb publicó un trabajo sobre el movimiento de los planetas rocosos del Sistema Solar en el que observó anomalías similares a las del perihelio de Mercurio en todos los planetas rocosos del Sistema Solar, e incluso en la Luna, aunque mucho más pequeñas. La ley de Hall no daba cuenta de estas otras anomalías. Newcomb demostró que la nueva ley de gravitación universal de Hall no era la respuesta correcta, pero puso en el candelero la posibilidad de que una nueva ley de gravitación universal pudiera ser la respuesta correcta.
La teoría más precisa que explicaba las anomalías de los perihelios de los planetas rocosos fue propuesta en 1906 por el astrónomo Hugo von Seeliger: una distribución de masa alrededor del Sol con una inclinación respecto de la eclíptica de 7º que además era responsable de la luz zodiacal. Esta explicación daba cuenta de todas las anomalías observadas y fue considerada correcta hasta 1919 cuando un eclipse solar confirmó la teoría de Einstein que ya había dado una respuesta alternativa al corrimiento del perihelio en 1915. La hipótesis de Seeliger nunca fue una oposición fuerte a la teoría de Einstein ya que la masa necesaria para explicar la anomalía era incompatible con la baja luminosidad de la luz zodiacal, como descubrió en 1915 el astrónomo Erwin Freundlich que, en palabras del propio Albert Einstein, fue su mano derecha astronómica (Seeliger trató de estudiar un eclipse en 1916 para confirmar la teoría de Einstein pero la I Guerra Mundial se lo impidió). Según los historiadores, sin el trabajo de Freundlich Einstein nunca hubiera sabido que la hipótesis de Seeliger no era un obstáculo para el desarrollo de su propia teoría y que explicar la anomalía del perihelio de Mercurio debía ser uno de los objetivos clave de su teoría general de la relatividad. Aún así, la hipótesis de Seeliger sobrevivió y fue uno de los argumentos fundamentales de los detractores de Einstein hasta 1919, cuando quedó demostrada la teoría de Einstein gracias a un eclipse (pero esto es otra historia).
 La idea de Hall de modificar las leyes de la gravedad newtoniana se enmarca en el contexto de las nuevas teorías de la gravedad que se volvieron muy populares a finales del s. XIX por analogía con la nueva electrodinámica desarrollada por Maxwell y coetáneos. La ley de Coulomb para la fuerza entre dos cargas eléctricas en movimiento se modifica con la adición de términos que dependen de la velocidad. Por analogía, se realizaron muchas propuestas de modificaciones similares para la fuerza gravitatoria entre dos masas en movimiento. Laplace ya lo hizo en 1805 como mero ejercicio teórico, pero a finales del s. XIX cada nueva ley propuesta para la fuerza entre dos cargas implicaba por analogía una nueva propuesta para la fuerza gravitatoria. Hubo muchas propuestas, como las de Weber, Riemann, Gauss, Clausius y Ritz (al final fue Lorentz quien obtuvo la fórmula correcta en 1892, pero esto también es otra historia). Por ejemplo, la propuesta de fuerza gravitatoria de Holzmuller en 1870 se basada en la fuerza entre cargas de Weber (1846). Esta nueva ley gravitatoria se aplicó a la anomalía del perihelio de Mercurio en 1872, cuando Tisserand demostró que predecía solo 14″ por siglo (mucho menos de lo observado). La ley de Riemann(-Liman-Lévi) predecía 28» (también menor de lo observado). Todas estas nuevas propuestas predecían anomalías menores de 14″ por siglo para el avance del perihelio de Mercurio, mucho menores de la observada por Newcomb.
La idea de Hall de modificar las leyes de la gravedad newtoniana se enmarca en el contexto de las nuevas teorías de la gravedad que se volvieron muy populares a finales del s. XIX por analogía con la nueva electrodinámica desarrollada por Maxwell y coetáneos. La ley de Coulomb para la fuerza entre dos cargas eléctricas en movimiento se modifica con la adición de términos que dependen de la velocidad. Por analogía, se realizaron muchas propuestas de modificaciones similares para la fuerza gravitatoria entre dos masas en movimiento. Laplace ya lo hizo en 1805 como mero ejercicio teórico, pero a finales del s. XIX cada nueva ley propuesta para la fuerza entre dos cargas implicaba por analogía una nueva propuesta para la fuerza gravitatoria. Hubo muchas propuestas, como las de Weber, Riemann, Gauss, Clausius y Ritz (al final fue Lorentz quien obtuvo la fórmula correcta en 1892, pero esto también es otra historia). Por ejemplo, la propuesta de fuerza gravitatoria de Holzmuller en 1870 se basada en la fuerza entre cargas de Weber (1846). Esta nueva ley gravitatoria se aplicó a la anomalía del perihelio de Mercurio en 1872, cuando Tisserand demostró que predecía solo 14″ por siglo (mucho menos de lo observado). La ley de Riemann(-Liman-Lévi) predecía 28» (también menor de lo observado). Todas estas nuevas propuestas predecían anomalías menores de 14″ por siglo para el avance del perihelio de Mercurio, mucho menores de la observada por Newcomb.
 La expresión correcta (la que obtuvo más tarde Einstein) para la anomalía del avance del perihelio de los planetas fue obtenida por primera vez gracias a la teoría de la gravedad de un físico alemán casi desconocido, el maestro de escuela Paul Gerber, publicada en 1898 en Zeitschrift fur Mathematik und Physik 43: 93–104, y en 1902 en Programmabhandlung des städtischen Realgymnasiums zu Stargard i. Pomm., 1902 (reimpreso en 1917 en Annalen der Physik 52: 415–444). La derivación era bastante poco clara y años más tarde se descubrió que contenía errores (que pueden ser corregidos). Aún así, obtuvo la fórmula correcta muchos años antes que Einstein (que la obtuvo en 1915). Su idea era aplicar una teoría de potenciales retardados similar a la utilizada en electromagnetismo bajo la hipótesis de que la gravedad se propaga a una velocidad finita, que Gerber calculó que coincidía con la velocidad de la luz en el vacío. El artículo de Jaume Giné contiene una derivación en notación moderna de la fórmula para el perihelio de Mercurio. Tras la reimpresión del artículo de Gerber en 1917 varios detractores de Einstein le acusaron de plagio. Einstein siempre dijo que él desconocía el oscuro trabajo de Gerber, pero que incluso si lo hubiera conocido no le habría influido a la hora de desarrollar su teoría y de afirmar que su fórmula para la anomalía confirmaba su teoría general de la relatividad.
La expresión correcta (la que obtuvo más tarde Einstein) para la anomalía del avance del perihelio de los planetas fue obtenida por primera vez gracias a la teoría de la gravedad de un físico alemán casi desconocido, el maestro de escuela Paul Gerber, publicada en 1898 en Zeitschrift fur Mathematik und Physik 43: 93–104, y en 1902 en Programmabhandlung des städtischen Realgymnasiums zu Stargard i. Pomm., 1902 (reimpreso en 1917 en Annalen der Physik 52: 415–444). La derivación era bastante poco clara y años más tarde se descubrió que contenía errores (que pueden ser corregidos). Aún así, obtuvo la fórmula correcta muchos años antes que Einstein (que la obtuvo en 1915). Su idea era aplicar una teoría de potenciales retardados similar a la utilizada en electromagnetismo bajo la hipótesis de que la gravedad se propaga a una velocidad finita, que Gerber calculó que coincidía con la velocidad de la luz en el vacío. El artículo de Jaume Giné contiene una derivación en notación moderna de la fórmula para el perihelio de Mercurio. Tras la reimpresión del artículo de Gerber en 1917 varios detractores de Einstein le acusaron de plagio. Einstein siempre dijo que él desconocía el oscuro trabajo de Gerber, pero que incluso si lo hubiera conocido no le habría influido a la hora de desarrollar su teoría y de afirmar que su fórmula para la anomalía confirmaba su teoría general de la relatividad.
Lo curioso de la historia de la ciencia es que este tipo de casos ocurren muy a menudo. Sobre todo entre físicos teóricos. Un físico obtiene un resultado pero no sabe defenderlo adecuadamente ante la comunidad. Más tarde es obtenido de forma independiente por otro u otros. No hay que exagerar y no hay que afirmar, por mor de la historia de la ciencia, que la fórmula de Einstein para la anomalía debe llamarse fórmula de Gerber-Einstein. Aunque disguste a muchos, la teoría de Einstein es la teoría correcta y la teoría de Gerber es una mera anécdota. Una teoría post-newtoniana anterior a Eddington y anterior a la relatividad especial.


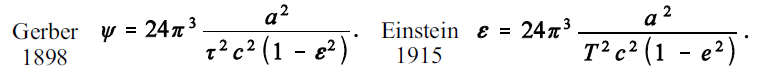
Hola,es posible formular una teoria relativista de la gravitacion basada en la RE en la cual se explican cuantitativamente los tres tests relativistas
http://www.telefonica.net/web2/casanchi/fis/teogravi01.htm
Se obtiene la formula para la energia potencial en la forma:
U = – GM.Et(inf)/c²(r-GM/c²)
Et(inf)=energia total relativista a infinita distancia de la fuente del campo gravitatorio M
A ver, no nos dejemos llevar por el entusiasmo de las teorías conspirativas.
Einstein desarrolló toda una teoría general de la Relatividad, y tras eso, la aplicó a la anomalía de Mercurio a modo de comprobación, y obtuvo la misma fórmula que Gerber. No tienen nada que ver ambos asuntos: sacarse una fórmula de la chistera y dar en el clavo, frente al derivarla como caso particular de una teoría general desarrollada de forma independiente.
Jose, la fórmula «correcta» era conocida desde mediados del siglo XIX, pues basta ajustar la precesión observada para obtenerla (redondeando las constantes a números enteros). El problema era cómo deducirla; muchos trataron de hacerlo usando fuerzas gravitacionales modificadas análogas a fuerzas de Coulomb modificadas propuestas por F. Neumann (1845), W. Weber (1846) y B. Riemann (1861). Ni Gerber (1898) ni nadie que le precedió obtuvo la fórmula correcta, que tiene infinitos términos y fue obtenida por Einstein; la fórmula de Gerber y la de Einstein solo coinciden en el primer término, siendo el segundo diferente. Me gustaría dejar claro este punto, la fórmula correcta es la que se deduce de la teoría de Einstein, mientras que la fórmula «correcta» de Gerber es solo una aproximación, derivada ad hoc, a ella.
Hola Francis. Tengo una duda: cuál sería la precesión de la órbita en un satélites artificial geoestacionario?
Por lo que pude leer la.misma es circular….entonces al ser cerrada no habria precesión de la órbita, geométricamente no puede haberlo…. entonces cuál sería la geodesica asociada a esta órbita geoestacionaria?
Al ser cerrada, no habria una trayectoria que variará espacio temporalmente, como en el caso de Mercurio….Me intriga saber que predice la teoría de la Relatividad General para un satélite geoestacionario.
Saludos desde Argentina
Yazu, lo primero, se observa precesión en satélites geoestacionarios porque la Tierra no es una esfera (es un geoide) y porque influyen la gravitación de la Luna y del Sol en su órbita; por ello se realizan correcciones de la órbita de forma periódica (un Δv ~ 50-55 m/s por año). Los efectos de la relatividad general para la órbita de un satélite geoestacionario son despreciables (basta usar la gravitación de Newton); sin embargo, para los que incluyen un reloj atómico hay que incluir una corrección debida a la dilatación del tiempo (similar en orden de magnitud a la necesaria en los satélites de GPS, que no son geoestacaionarios).
No me queda clara la explicación del avance del perihelio de Mercurio, el porqué sucede.
Jaime, para que la órbita en el problema de dos cuerpos sea cerrada es necesario que la fuerza depende de la inversa del cuadrado de la distancia (como en la teoría de Newton); en la Naturaleza, y en la relatividad general, la fuerza presenta correcciones que dependen del inverso del cubo de la distancia, luego la órbita no puede ser cerrada y por ello se observa una precesión del perihelio. En el caso del perihelio de Mercurio, la precesión observada es de 5599.7 segundos de arco por siglo; 5025.6 es debido a la precesión de los equinoxios (al sistema de coordenadas usado); 531.4 es debido a la gravitación de los demás planetas del Sistema Solar; 0.0254 es debido a la forma del Sol (su momento cuadripolar); y 42.98±0.04 es debido a lo que te acabo de contar (descrito por la relatividad general).