La idea de usar latas de refresco para crear un metamaterial acústico que actúa como superlente no es nueva (en mi blog en 2011). Recuerda que una superlente logra enfocar una señal (óptica o acústica) por debajo de la mitad de su longitud de onda (su límite de difracción). El nuevo metamaterial aprovecha la resonancia de Helmholtz para concentrar la señal acústica en la apertura de una lata. La novedad de este trabajo es que no usa ondas evanescentes, lo que facilita que los profesores de física puedan explicar la teoría de este experimento a sus alumnos. Por ello, no hay excusa para que no ilustren a sus alumnos los metamateriales usando latas de su refresco favorito (por cierto, todas las latas deben estar vacías).
El artículo técnico es A. A. Maznev et al., «Extraordinary focusing of sound above a soda can array without time reversal,» arXiv:1411.1016 [physics.class-ph]. El anterior artículo técnico es Fabrice Lemoult et al., «Acoustic Resonators for Far-Field Control of Sound on a Subwavelength Scale,» Phys. Rev. Lett. 107: 064301, 3 Aug 2011. La idea de las superlentes parte del trabajo de J. B. Pendry, «Negative Refraction Makes a Perfect Lens,» Phys. Rev. Lett. 85: 3966, 30 Oct 2000.
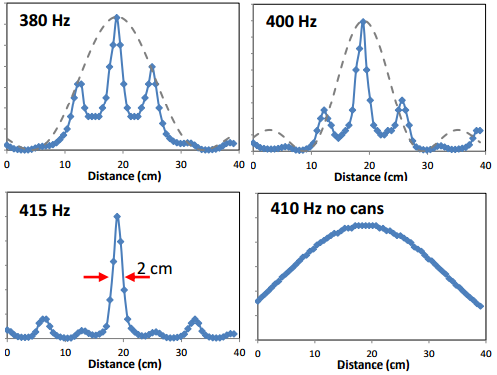
Las latas de refresco se colocan en un patrón hexagonal rodeadas de seis altavoces situados de forma simétrica. Cada lata tiene un volumen de 330 ml y una apertura superior de unos 4 cm². La frecuencia de resonancia de Helmholtz de esta configuración es de 420 Hz. Para medir la intensidad del campo acústico se ha suspendido un micrófono a una altura de 12 ± 2 mm por encima de las latas. Un sistema mecánico permite mover el micrófono en horizontal durante una trayectoria recta de unos 40 cm siguiendo la diagonal de la configuración (línea verde en la foto de la derecha en la figura que abre esta entrada). Para las medidas se ha introducido el sistema en una cámara anecoica (cuyas paredes absorben las reflexiones producidas por las ondas acústicas).
Esta figura muestra la intensidad acústica en la diagonal del metamaterial (línea verde). Sin latas, el pico de intensidad tiene una FWHM (semianchura a la mitad de la amplitud máxima) de 31 cm para 410 Hz, es decir, el 37% de la longitud de onda. Un cálculo teórico (que requiere usar funciones de Bessel porque la simetría es circular) ofrece un valor del 36% de la longitud de onda, en buen acuerdo con la medida experimental. Cuando se introduce el metamaterial de latas de refresco el pico se concentra hasta una FWHM de sólo 2 cm a 415 Hz, es decir, un 1/40 de la longitud de onda.
El artículo discute la teoría que explica el fenómeno. Básicamente el aire de cada lata actúa como un resonador de Helmholtz tridimensional que se acopla al aire en cada apertura superior que actúa como un resonador de Helmholtz bidimensional secundario. Esta combinación de un sistema tridimensional y otro bidimensional es el secreto de la configuración. El modelo teórico es sencillo, pero omitiré los detalles.
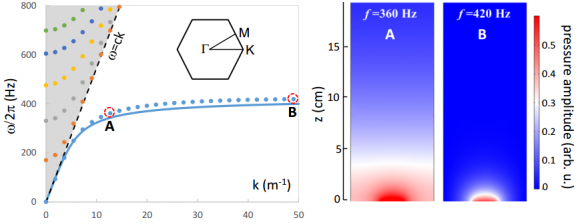
Los profesores de física computacional (o de métodos numéricos) disfrutarán sabiendo que el artículo presenta un modelo de elementos finitos del sistema (los autores han usado el simulador multifísica COMSOL pero el modelo se puede implementar fácilmente en Matlab). La onda sonora que se propaga por encima de la configuración hexagonal de latas es un modo guiado (casi) bidimensional cuya longitud se acorta al acercarse la frecuencia de excitación de la resonancia de Helmholtz para el sistema de resonadores bidimensionales (aire localizado en las aperturas de las latas). Por ello el metamaterial actúa como superlente para ondas acústicas superficiales en la capa de aire en contacto con la parte superior de las latas. Esta figura muestra las curvas de dispersión calculadas por elementos finitos y el campo acústico en dos puntos.
Lo bonito es que este metamaterial puede ser usado para ilustrar el teorema de Bloch de la teoría de bandas electrónicas en sólidos. Por ello también será útil para los profesores de física del estado sólido, que podrán disfrutar de un sistema tridimensional de fácil construcción para realizar experimentos a sus alumnos.
En resumen, un bonito ejemplo de un metamaterial macroscópico que actúa como superlente (aunque sólo para ondas acústicas casi-bidimensionales). Por supuesto, en sentido estricto, el sistema no viola el límite de la difracción, pero no importa, pues sirve para ilustrar la teoría de bandas en sólidos y la teoría de resonancias en sistemas físicos casi-periódicos.




estooo… cómo?
Reconozco que no lo he leído completo sino a saltos, pero no tengo ni idea de lo que pretende este artículo ni para qué sirven las latas…
Supongo que es un texto para iniciados, y habitualmente los artículos de esta web suelen ser más divulgativos.
En fin. Gracias de todas formas, seguro que a mucha otra gente le resultará interesante.
Carlos, ¿sabes lo que es un metamaterial? Busca en la wikipedia. ¿Para qué sirve este metamaterial acústico con latas? La verdad, para nada, más allá de ilustrar a los alumnos las propiedades de los metamateriales en un laboratorio de física.
Hola Francisco,
Espero que no tomes a mal el comentario, solamente quería reflejar mi desconcierto por un artículo del que no entendía nada. Normalmente en Naukas se suelen dar explicaciones más «a pie de calle», o al menos con una introducción para los profanos y no por ello menos rigurosas o detalladas. Muchas veces empiezo a leer algo y hacia la mitad ya no lo entiendo, pero al menos «sé de qué va».
Supongo que una breve explicación sobre lo que son los metamateriales (gracias por el enlace) y poner en términos llanos en qué consiste el experimento y qué resultado se observa (y me refiero a observar en un sentido literal) hubiera ayudado a hacerlo más comprensible. Todo ello por supuesto sin perjuicio de todo el detalle que ofreces.
Es una sugerencia constructiva, ni siquiera una crítica, que creo que te serviría para incrementar el público que pueda acercarse a este artículo.
Disculpa si el tono del primer mensaje no fue el correcto.
Un saludo,
Carlos
Carlos, es normal que la forma de divulgar de Francis te resulte peculiar, comparada con el resto de la página. Tan sólo es cuestión de cogerle el punto.
Las materias que trata suelen ser muy complejas. Estamos acostumbrados a la ciencia simple y elegante que se puede explicar alegando a conocimientos de una educación básica, o mediante analogías. Eso está bien para algunas cosas, pero para otras no vale. La ciencia a éste nivel se explica y se entiende por los principios que la definen, y es difícil ser divulgado al respecto sin tener conocimientos previos.
Además, Francis habla de actualidad científica; de nuevos conociemientos que se basan en otros ya existentes. Obviamente se centra en lo primero y no en lo segundo. Si en cada artículo tuviera que explicar los principios científicos de las cosas sobre las que habla, no terminaría nunca.
Por otro lado, hay que entender que sus artículos no son lugar para aprender ciertas cosas. Como él mismo te recuerda, para eso está internet (y la universidad). Exigen pues sus lecturas un trabajo por parte del divulgado. Para mí, que soy un curioso sin título, supuso un shock al principio, pero luego lo entendí y lo acepté. Si el tema del que habla te interesa, tu curiosidad te llevará a investigar sobre él. Si no te interesa, por lo menos sabes que estas cosas existen, y que son complejas, algo que a mí por lo menos me hace apreciar más el trabajo de las personas que se dedican a ello.
Carlos, si miras en Wikipedia lo que es una resonancia Helmholtz, entenderás mejor el fenómeno
físico https://en.wikipedia.org/wiki/Helmholtz_resonance
edusenx, supongo que primero deberíamos poner en común lo que entendemos por divulgación científica.
En mi opinión este artículo no es divulgativo, al menos si hacemos caso a la definición de la wikipedia: «es el conjunto de actividades que interpretan y hacen accesible el conocimiento científico al público general…» ya que parte de la suposición de que el lector entiende y conoce los por menores de lo que se explica.
Claro, si suponemos que los receptores del artículo son profesores de física interesados en usar el experimento en sus clases, pues entonces sí.
Hola, si quisiese verlo en wikipedia para que iba a leer esto. Esta way pero para mi gusto falta explicar lo que es un resonador de helmholtz y muchas cosas carecen de rigor. Como poner una imagen de un sistema mecánico(masa, muelle) y no explicar las analogías con el sistema acústico que es el resonador. ni explicar de que elementos físicos del resonador depende la frecuencia de resonancia como son la sección de la abertura, la longitud del cuello o el volumen de la cavidad interior, o si la abertura tiene o no pestañas. Decir para que sirven… Ya que que siendo una de sus utilidades el acondicionamiento acústico, la frecuencia de resonancia y los parámetros de los que esta dependen son relevantes.
Pedrito, busca lo que te cuento en la wikipedia. Si lo encuentras, abandona este blog. Si no lo encuentras, busca en la wikipedia las cosas que menciono y que no explico, porque esas vienen en la wikipedia.