Tras las colisiones del LHC Run I mucha gente ha dado por muerta a la extensión supersimétrica mínima del modelo estándar, el modelo MSSM. Quizás demasiado pronto. Su versión natural ha sido casi descartada, pero su versión casi-natural sigue viva y coleando. Esta figura muestra que lo casi-natural en el modelo MSSM (que la mezcla de stops sea mínima) implica que aún no deberíamos haber encontrado el stop (el compañero supersimétrico del quark top). Su masa más razonable ronda los 10 TeV/c², más allá del alcance del LHC. Por tanto, el MSSM predice que no deberíamos haberlo observado y no lo hemos observado.
Como lo lees… el LHC nunca podrá desbancar el modelo MSSM casi-natural. Y por ende la supersimetría (recuerda que hay decenas de modelos supersimétricos más complicados que el MSSM). Para un resumen de la situación recomiendo leer a Alessandro Strumia, «Theory summary of Moriond Electro-Weak 2015,» arXiv:1504.08331 [hep-ph]. Detalles técnicos en su artículo Emanuele Bagnaschi et al., «Higgs Mass and Unnatural Supersymmetry,» JHEP 1409: 092 (2014), doi: 10.1007/JHEP09(2014)092, arXiv:1407.4081 [hep-ph], y en Javier Pardo Vega, Giovanni Villadoro, «SusyHD: Higgs mass Determination in Supersymmetry,» arXiv:1504.05200 [hep-ph]. Me ha recordado que tenía que hablar de este tema Jester, «Weekend Plot: Higgs mass and SUSY,» Résonaances, 30 May 2015.
La partícula compañera del quark top, llamada squark top o simplemente stop, es un sfermión, es decir, un bosón escalar (espín cero) como el Higgs. En el modelo estándar el quark top es el más pesado. En el modelo MSSM el stop es el squark más ligero. Lo natural para que la supersimetría resuelva el problema de la jerarquía asociado al bosón de Higgs es que el stop tenga una masa en la escala electrodébil que está explorando el LHC. Por ello la esperanza de muchos era que el LHC Run I descubriera esta spartícula. El LHC ha descartado que exista un stop con masa inferior a unos 700 GeV/c² (recuerda que el Higgs tiene una masa de 125 GeV/c²). ¿Ha matado el LHC la supersimetría MSSM natural?
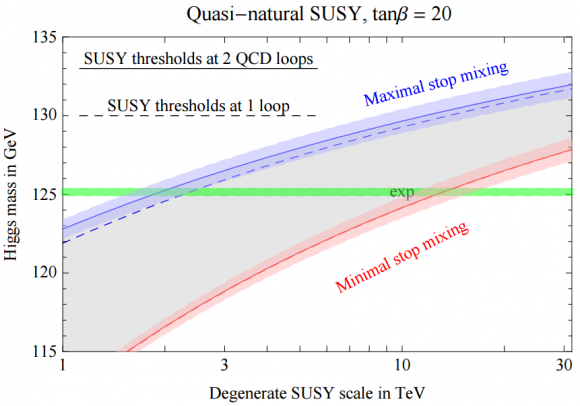
En realidad el stop se puede esconder al LHC. El modelo MSSM conserva la paridad R, que diferencia partículas y spartículas. La paridad R predice que hay stop de quiralidad izquierda (L-stop) y derecha (R-stop). Igual que ocurre con la oscilación de los neutrinos, cuyos estados masivos son una mezcla de los tres sabores, los estados masivos de los stops pueden ser una mezcla de ambas quiralidades. El parámetro de mezcla de los stops caracteriza esta mezcla. Como muestra esta figura, si el parámetro de mezcla es pequeño, la masa del stop debe superar los 10 TeV/c² para un Higgs de 125 GeV/c². El LHC con colisiones a 14 TeV c.m. no puede descubrir nuevas partículas con una masa mayor de 5 TeV/c². Por tanto el stop (la partícula supersimétrica del MSSM con menor masa) estaría más allá de su alcance.
La supersimetría predice la existencia de múltiples bosones de Higgs (cinco en el modelo MSSM). La masa de estos nuevos bosones de Higgs puede ser mucho mayor que la del Higgs descubierto en 2012. Sin embargo, su existencia se puede probar de forma indirecta, ya que median ciertas desintegraciones exóticas de los bosones Z. Por ahora dichas desintegraciones tienen una probabilidad por debajo de la sensibilidad de los detectores del LHC (unos dos órdenes de magnitud por debajo). El LHC Run II no logrará una luminosidad suficiente para observar estas desintegraciones y habrá que esperar hasta el LHC Run III.
La verdad es que la supersimetría tiene mucho hueco para esconderse (entre mil GeV y un trillón de GeV). Piensa que lo natural es observarla a mil GeV el borracho que busca las llaves bajo la farola del LHC. Pero quizás ya hemos observado la supersimetría. Lo natural son los campos bosónicos (como el Higgs, el fotón o el gravitón). En rigor, los fermiones no son naturales. Quizás la existencia del electrón es la prueba más firme de la supersimetría. Quizás no somos conscientes de ello pero ya logramos descubrir la primera partícula supersimétrica hace más de un siglo. Lo natural es que así sea.




Perdone Francis:
Ya lo comenté en Twitter pero lo comento aquí (Usted disculpe).
¿A qué exactamente se refiere con decir: «En rigor los fermiones no son naturales»?
Me ha intrigado mucho su comentario, ojalá pueda comentar algo al respecto. Gran entrada por cierto.
Ramiro, varios expertos en supersimetría han dicho en las últimas décadas que la supersimetría es «natural» y que los fermiones existen porque existe la supersimetría; lo «natural» en un universo sin supersimetría es que no existan los fermiones (si un físico teórico piensa en un nuevo campo, siempre piensa en un campo bosónico, y sólo si no le queda otro remedio, se atreve a regañadientes a considerar uno fermiónico). Para muchos expertos en supersimetría la existencia de los fermiones es una prueba de que el universo es supersimétrico.
Saludos
Francis
Gracias por la explicación no tenía ni idea de que estaba así de malita la cosa para los fermiones. Todo mi apoyo para ellos y sus familias, con especial cariño para leptones y quarks .
Creo que los Bosones se pasan de «abusones», a partir de ahora las partículas las clasificaré en Fermiones y «abusones».
(Madre mía como esta el mundo como diría mi abuela)
Con perdón, creo que aquí se mezclan dos cosas.
1) La existencia de fermiones es una consecuencia genérica de la teoría de la relatividad especial. La supersimetría no tiene nada que ver.
Tanto bosones como fermiones aparecen en pie de igualdad al estudiar las representaciones unitarias del grupo de Poincaré, que es el grupo de simetrías de la relatividad especial. Los posibles tipos de partículas vienen dados por estas representaciones (clasificación de Wigner), las cuales quedan etiquetadas por su masa (básicamente, cómo se comportan bajo traslaciones) y por su espín (cómo se transforman bajo rotaciones).
El espín, que aquí simplemente aparece como un invariante de teoría de grupos útil para etiquetar representaciones, es un número que puede ser tanto entero como semientero. Así que lo natural es que en una teoría relativista (por más que no sea supersimétrica) haya tanto bosones como fermiones. Lo antinatural sería que no hubiese uno de los dos, ya que no hay ninguna razón para suponer que la mitad de las representaciones del grupo de Poincaré no se realizan en la naturaleza.
2) Lo «raro» no es que haya partículas fermiónicas en la naturaleza, sino que no haya *generadores* fermiónicos en el grupo de simetrías del espaciotiempo.
Todos los generadores del grupo de Poincaré son bosónicos. Metafóricamente, puedes decir que el grupo de Poincaré es «una tabla de multiplicar de los números pares». Si eso no te gusta y extiendes el grupo de Poincaré para incluir generadores fermiónicos («los números impares»), obtienes el álgebra de supersimetría. En este sentido, la supersimetría puede verse como una generalización muy natural del grupo de simetrías de la relatividad especial. Y la misma teoría de representaciones que antes te decía que en la naturaleza hay partículas con masa y con espín (independientes uno de otro), ahora te dice que para cada masa tienes una partícula con espín entero y otra con espín semientero.
Las razones por las que un físico puede preferir los campos bosónicos a los fermiónicos son en general técnicas (dificultad de trabajar con variables de Grassmann, etc), no fundamentales.
Gracias, DouDou por tu comentario.
Muchas gracias Dou Dou, da gusto leer explicaciones de este nivel. Ya me extrañaba a mi, jeje. Un saludo.