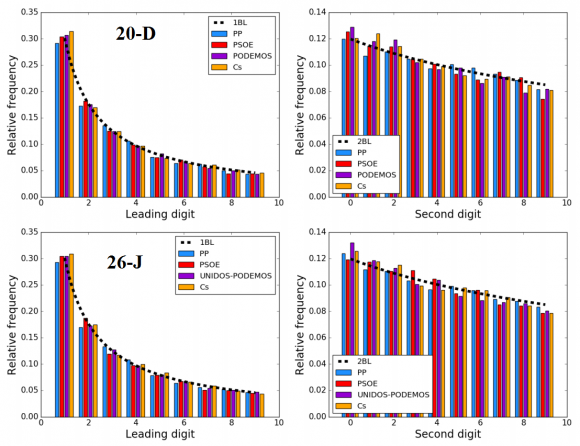
La ley de Benford para el primer (1BL) y el segundo (2BL) dígitos se usa en el análisis forense de un resultado electoral. El análisis del 100% de los votos en todos los municipios españoles para las elecciones nacionales del 20 de diciembre de 2015 y del 26 de junio de 2016 está en total acuerdo con dichas leyes. No hay desviaciones significativas que puedan ser achacadas a algún tipo de fraude. Tampoco hay desviaciones sistemáticas entre el 20-D y el 26-J. Los resultados estadísticos son cualitativamente idénticos en ambas elecciones.
El artículo es Juan Fernández-Gracía (Univ. Harvard) y Lucas Lacasa (Queen Mary, Univ. Londres), «Forensic analysis of spanish 2015 and 2016 national elections,» arXiv:1607.02841 [physics.soc-ph].
Estos histogramas muestran la aplicación de la ley de Benford del primer (izquierda) y del segundo (derecha) dígitos para los resultados por municipios (más de 8000) en las elecciones del 20-D (arriba) y del 26-J (abajo) para los cuatro grandes partidos PP (azul), PSOE (rojo), Podemos & Co. o Unidos Podemos (morado), y Ciudadanos (naranja). Los resultados son estadísticamente idénticos.
Uno de los autores, Se ha realizado un contraste de hipótesis para determinar si los resultados por municipios en las dos elecciones siguen la ley de Benford. Para la ley del primer dígito (1BL) el test rechaza dicha hipótesis para el PP con un 99% de confianza estadística (datos en rojo), pero acepta dicha hipótesis para el resto de los partidos. Para la ley del segundo dígito (2BL), el test rechaza que PSOE y PODEMOS sigan la ley, pero con menos del 95% de confianza (en azul en la tabla). Estos resultados no son concluyentes porque con otros niveles de agregación salen cosas diferentes. Luego estas desviaciones no son ni sistemáticas ni significativas, y no se pueden interpretar como indicativas de algún tipo de fraude.
Por supuesto, el análisis forense de elecciones usando la ley de Benford no está exento de controversia. Para los expertos siempre deber se considerado como complementaria de otros análisis basados en correlaciones en el porcentaje de participación y de votos por cada municipio. El análisis forense de estas correlaciones para las elecciones del 20-D y del 26-J tampoco arroja indicios de fraude.
Esta figura para las elecciones del 26-J muestra un mapa de color con el porcentaje de municipios en los que cada partido político ha recibido cierto porcentaje de votos (voteshare) en función de la participación relativa (turnout). La figura correspondiente a las elecciones del 20-D es muy similar (por ello la omito). Una distribución bimodal con una acumulación grande en la esquina superior derecha es indicativo de fraude. No se observa, luego se descarta cualquier tipo de fraude.
Destaca en estas figuras el comportamiento bimodal del PP. Se deduce que existen dos tipos de municipios que han votado al PP. La región pequeña con porcentajes de voto al PP inferiores al 20% corresponde a pequeños municipios en las regiones con aspiraciones independentistas (Cataluña y País Vasco). La región grande corresponde al resto de los municipios. Por tanto se descarta cualquier tipo de fraude asociado a esta bimodalidad.
En resumen, el análisis forense mediante la ley de Benford de las pasadas elecciones descarta cualquier tipo de fraude. Los autores del estudio afirman que pretenden realizar un análisis similar con los resultados históricos de todas las elecciones en nuestro país tras la transición. Habrá que estar al tanto de sus resultados.




Muchas gracias por el resumen.
Creo que la interpretación de test chi2 la has hecho al revés Francisco, justamente para el caso que discutes (municipios) el test rechaza la hipótesis de que se ajusta a una Benford con una confianza del 99% en el caso del PP (1BL) y con una confianza menor (95%) en el caso de Podemos y PSOE para 2BL. Estos resultados no son sin embargo concluyentes porque con otros niveles de agregación salen cosas diferentes.
Saludos,
Lucas
Gracias, lo aclararé.
Da la impresion, por lo que se dice en el articulo, de que convendria separar, ademas de los casos con grandes partidos nacionalistas, el analisis de grandes distritos del de los pequeños, para aislar el caso de «total turnout and large voteshare». Esto de los distritos pequeños se ve espectacularmente en un plot que se podria llamarse «de victoria del bipartidismo»: el heatmap del plano de porcentaje de votos PP-PSOE, que presenta dos clusters: los grandes distritos cercanos a una diagonal con suma 65%, y los pequeños formando una diagonal clavada con suma por encima el 80% (en mi blog tengo un plot parecido pero la separacion grandes/pequeños es por total de votos a los partidos representados, no por la participacion total del distrito)
Alejandro, muy interesante. Recomiendo a los lectores visitar las últimas entradas de tu blog sobre estadística electoral, como «metroscopia, microdatos, links y ya vale», 11 Jul 2016, «sí, aún más estadísticas de las elecciones», 08 Jul 2016, y muchas más.
sin ánimo de ofender a los autores ni a ningún matemático y, hablando desde una relativa ignorancia, tan solo quiero manifestar mis dudas:
Personalmente la ley de Benford no me parece nada más que una curiosidad matemática, fruto de una ley subyacente de invariancia de escala. Y sin embargo, cada dos por tres aparecen publicaciones usando test estadísticos bastante simplistas para aludir o refutar fraude.
Pero de verdad éste test a servido nunca para detectar fraude? Alguien ha estudiado el ratio de acierto?
A mi parecer, tan solo un numero muy limitado de mecanismos de ‘fraude’ asociados a una torpe ‘cocina’ de números darían positivo en el test de Benford. Cualquier mecanismo basado en técnicas estocásticas pasaría el test sin ningún problema.
Conocés algún estudio similar, pero de las elecciones presidenciales de Austria donde hubo tremendo fraude? Porque todo muy cómodo queda en decir «no pasó nada», cuando además nadie discute eso. Pero me gustaría ver si sus análisis les llegan a dar un «no pasó nada» en Austria; o si realmente ellos también detectan el fraude (como lo confirmó la Corte Suprema, en por lo menos 70,000 votos «irregulares»). Sería un buen escenario de aplicación para un análisis forense y no leí acerca de ninguno de ellos presentado como prueba (a favor o en contra) de la impugnación a las elecciones -elecciones que a todo esto volverán a ser realizadas en Octubre-. saludos
Francisco M, yo no conozco ninguno sobre las elecciones en Austria el 24 de abril de 2016, pero el artículo más famoso sobre estos temas está firmado por austríacos: Peter Klimek, Yuri Yegorov, Rudolf Hanel, Stefan Thurner, «Statistical detection of systematic election irregularities,» PNAS 109: 16469-16473 (2012), doi: 10.1073/pnas.1210722109, arXiv:1201.3087 [physics.soc-ph]. Quizás publiquen algo en los próximos meses.
No se si los autores han dejado en algun sitio los datos en bruto para trabajarlos. Los del 2016 han cirtulado por meneame y he puesto por el github un ejemplo de como manejarlos desde python https://gist.github.com/arivero/c953ebb0a1baf66abc5bb2303a8a9b6a incluyendo el json que ha circulado. De los del 2015 quiero pensar que se podia volcar una hoja de calculo, pero puede que los este confundiendo con las municipales.
Analizando un poco el estudio me da la impresión de que se dejan muchos flecos. Hay unos cuantos miles de municipios (>10.000) que no se analizan en detalle y en los que parece haber un baile misterioso de unos 100 votitos, o eso dicen. Me gustaría poder disponer de los datos en formato json csv o similar del 20D y del 26J para comprobar esa posibilidad, si alguien sabe de donde se pueden sacar prometo compartir unas cuantas SQLs 😉
Por otra parte, para muchos, la sorpresa del 26J parece tener cabida en lo de que «¡Que viene el lobo!» aun sigue funcionando y esto, en los pueblos pequeños alguien lo comenta una tarde en la tasca y al segundo trago todos convencidos. No se … ¿Quizá a alguno os tembló la mano al ver lo del Brexit?
Interesante será cuando analicen las del 28A de este año.
Me gustaría contactar con Ximeno, o con quien este interesado en aplicar Benford a las elecciones 2019. los datos de las mismas están publicados por el Ministerio del Interior. Si alguien tiene interés que escriba a franciscalapuerta@hotmail.com
Hola:
Este artículo indica que no se puede aplicar la ley de Benford para predecir fraude o no debido a que las diferentes variables de los resultados de los distintos partidos no son independientes:
https://ichi.pro/es/la-ley-de-benford-no-prueba-el-fraude-en-las-elecciones-presidenciales-de-ee-uu-de-2020-224856324701146
También citan un artículo que indica lo siguiente:
«La Ley de Benford es problemática en el mejor de los casos como herramienta forense cuando se aplica a las elecciones … Su ‘tasa de éxito’ de cualquier manera es esencialmente equivalente al lanzamiento de una moneda, lo que la vuelve problemática en el mejor de los casos como herramienta forense y totalmente engañosa en el peor».
Fuente: Deckert, Joseph, Mikhail Myagkov, Peter C. Ordeshook. «La ley de Benford y la detección del fraude electoral». Análisis político 19.3 (2011)
Es paradójico pero puede ocurrir que que cumpla esta Ley puede indicar que se han manipulado los datos para que lo cumpla… o no.