La matemática ucraniana Maryna Viazobska nos hizo un gran regalo el pasado Día Pi, 14 de marzo de 2016. La solución al empaquetamiento de esferas en 8 dimensiones. La red de raíces del grupo de Lie excepcional E8 es el empaquetamiento más denso. Su demostración es tan elegante y tan fácil de entender que en pocos días inspiró la solución al problema en 24 dimensiones. La red de Leech es óptima.
Por desgracia su método de demostración no se puede generalizar a un número arbitrario de dimensiones. Aún así, sus ideas podrían inspirar la solución en cuatro dimensiones. Este problema, en apariencia tan sencillo, solo está resuelto en dimensiones 1, 2, 3, 8 y 24.
Su delicioso artículo es Maryna Viazovska, «The sphere packing problem in dimension 8,» arXiv:1603.04246 [math.NT]. Su generalización es Henry Cohn, Abhinav Kumar, …, Maryna Viazovska, «The sphere packing problem in dimension 24,» arXiv:1603.06518 [math.NT]. Una explicación para legos de las ideas clave de estas demostraciones nos la presenta Henry Cohn, «A conceptual breakthrough in sphere packing,» Notices of the AMS 64: 102-115 (Feb 2017), doi: 10.1090/noti1474, arXiv:1611.01685 [math.MG].
Esta entrada participa en la Edición 8.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit. Se podía participar entre los días 21 y 28 de febrero, comunicándolo con la etiqueta #CarnaMat81 vía las cuentas @eliatron y @CarnaMat.
La solución al problema del empaquetamiento de esferas en consiste en determinar la fracción de todo el espacio que puede ser cubierta por
-esferas idénticas con interiores disjuntos. Esta fracción se denomina densidad de empaquetamiento y su valor es el obvio en una, dos y tres dimensiones. En una dimensión el resultado es trivial e igual a la unidad. En dos dimensiones el resultado es bien conocido, el empaquetamiento de monedas con densidad
; fue probado por Thue en 1890, aunque la demostración con total rigor fue de Fejes Tóth en 1940. En tres dimensiones el resultado también coincide con el esperado, el empaquetamiento de naranjas con densidad
. Su demostración fue obtenida usando ordenadores por Hales en 1998 (publicada en 2005) y verificada usando lógica formal más tarde.
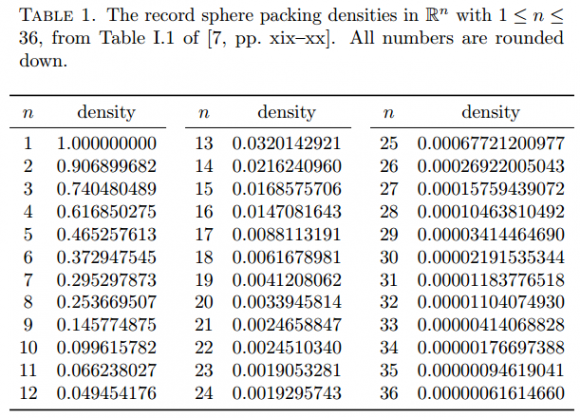
No se conocía la solución óptima al problema en más de tres dimensiones hasta el trabajo de Viazovska. Salvo para dimensión 8 y 24, aún se ignora dicha solución. Esta tabla muestra el récord de densidad de empaquetamiento en función de la dimensión (que solo los casos 1, 2, 3, 8 y 24 coincide con el valor óptimo). La densidad óptima es mayor de y menor de
, como probaron Kabatyanskii y Levenshtein en 1978. Como se observa la solución óptima decrece exponencialmente con la dimensión.
Mediante programación lineal basada en análisis armónico se pueden obtener cotas superiores a la densidad, como probaron Cohn y Elkies en 2003. Se hace un uso muy curioso de la fórmula de sumación de Poisson que relaciona la suma de los valores de una función diferenciable en la red de centros de las esferas y su transformada de Fourier en la llamada red dual. La técnica es muy sencilla y permite obtener la curva que muestra esta figura como cota superior de la densidad. Esta cota coincide con el valor exacto en dimensiones 8 y 24, un punto clave en la demostración de Viazovska. Sin embargo, se separa mucho para otras dimensiones.
Cohn y Elkies conjeturaron la existencia de funciones mágicas asociadas al problema de empaquetamiento óptimo. Estas funciones cumplen la igualdad entre la densidad óptima y la cota obtenida por optimización lineal. Esta figura muestra la función para dimensión ocho que ha construido Viazovska usando formas modulares. Cada red de empaquetamiento tiene asociada una función Theta dada por
.
Esta función analítica cumple para , que
,
.
En 24 dimensiones, para la red de Leech se tiene de forma similar que
,
.
Gracias a estas propiedades es posible construir las funciones mágicas de Cohn y Elkies. Y con ellas la prueba de que dichos empaquetamientos son óptimos.
No se sabe si estos resultados para 8 y 24 dimensiones pueden ayudar en la futura demostración en 4 dimensiones. Pero no parece un camino fácil. Por supuesto, para otras dimensiones todo apunta a que el camino a seguir será muy diferente.
Recomiendo el artículo de Cohn en Notices of the AMS que nos resume muy bien la idea de la demostración de Viazovska. Por supuesto, los matemáticos más intrépidos disfrutarán leyendo el artículo original de Viazovska. Sirva esta entrada para motivar a su lectura.





Tal vez esté mal que haga un comentario a la ligera pero cuando yo leo:
«La solución al empaquetamiento de esferas en 8 dimensiones. La red de raíces el grupo de Lie excepcional E8 es el empaquetamiento más denso. Su demostración es tan elegante y tan fácil de entender que pocos días inspiró la solución al problema en 24 dimensiones. La red de Leech es óptima.»
D=8 = 10 -2 y E8 y luego un vínculo con D=24 = 26 -2 … Se lee muy «Stringy». Antes de leer el paper pensé que me sorprendería mucho que la demostración no incluyera una mención al álgebra de Virasoro (o a álgebras de Kac Moody) y no estuviera repleto de formas modulares… ¡Y no me equivoqué!
Que maravilloso es que en el paper aparezca la función J y su expansión en serie de Fourier. Que mágico que un problema de geometría tenga vínculos tan fuertes con álgebra y con análisis complejo.
Que maravilla
Obviamente no entendí ni remotamente la demostración, pero la hojié esperando un resultado como «PI^2/SQR(20)» o algo similar, ¿al final obtienen un número? está ahí en el paper y le pasé por encima sin verlo?
Perdón, Gerardo, pero ¿de verdad no has visto la primera fórmula que aparece en la página 2? La que pone Δ8 = π^4 / 384. En la página 1 solo tienes fórmulas con la definición de la densidad de empaquetamiento que se usa. ¿No te habrás equivocado de artículo?
Por cierto, para 24 dimensiones la fórmula es Δ24 = π^12 / 12!
ups! si ahí está, es que estaba buscando al final, y no me molesté en leer/traducir el principio del paper (necesitaba que me llevaran como un niñito chiquito hasta el numerito)
Lo pone en la pagina 2 ∆8 =π^4/384≈ 0.25367.
Para dimensión 24 es π^12/12! = 0.0019295743.
Tengo entendido que la solucion de Hales la obtuvo el 1998, el 2005 fue el año en que aceptaron su publicación. En cuanto a Maryna Viazobska, próxima medalla fields?
Gracias, yomismo, por estar atento. Lo corrijo. Viazobska está en las quinielas para la Medalla Fields 2018.