
Los cristales de tiempo propuestos por Frank Wilczek en 2012 son físicamente imposibles. En un sistema disipativo la simetría traslacional del tiempo está rota (si no fuera así se conservaría la energía). Hoy en día se llama cristal de tiempo a un sistema periódico disipativo que oscila de forma sostenida gracias a un forzamiento externo. El cristal de tiempo será discreto si su frecuencia de oscilación es un subarmónico de la frecuencia de forzamiento; en otro caso se dice que es un cristal de tiempo continuo. Se publica en Science un sistema biestable en un condensado de Bose–Einstein (BEC) de átomos de rubidio ultrafríos dentro de una cavidad óptica y excitado por un láser externo. Gracias a la superradiancia de Dicke los átomos absorben fotones del láser y los reemiten como luz confinada en la cavidad; esta luz confinada induce una interacción interatómica que permite la emergencia de un orden espacial entre los átomos, que rompe la simetría continua de traslación espacial de los átomos (el BEC) dando lugar a una retícula bidimensional (un cristal espacial). En este sistema biestable los átomos en la red oscilan entre dos estados posibles con un periodo que cambia de forma aleatoria en cada realización del experimento. Gracias a esta aleatoriedad la frecuencia de la oscilación no depende de la frecuencia del láser, por lo que se afirma haber logrado un cristal de tiempo continuo.
Permíteme simplificar al máximo la física de la oscilación de los átomos entre dos configuraciones degeneradas (que tienen la misma energía, luego ninguna es preferible a la otra). En la primera configuración, los átomos atrapados en la cavidad óptica se sitúan en los mínimos de la retícula inducida por la luz del láser de bombeo. En estos mínimos emiten menos luz confinada en la cavidad y se reduce su interacción mutua. Esta libertad de movimientos les permite desplazarse hasta los máximos, la segunda configuración (que tiene la misma energía que la primera). En ella tienen mayor probabilidad de emitir luz confinada en la cavidad. Como resultado crece su interacción mutua y tienden a retornar a la primera configuración. Esta oscilación se repite dando lugar a un cristal de tiempo. Quizás te preguntes dónde se oculta la rotura de la simetría de traslación temporal necesaria para recibir dicho nombre. Obviamente, se trata de un sistema abierto con disipación, durante la oscilación hay una pérdida de átomos y de luz que escapan de la cavidad (luego la energía no se conserva). Como resultado, el ciclo solo se repite un número finito de veces, pues las pérdidas reducen las interacciones mutuas entre los átomos hasta un punto en el que es imposible la repetición de la oscilación.
Los cristales de tiempo me recuerdan la famosa frase comercial se acepta pulpo como animal de compañía. Le llamemos como le llamemos, el experimento realizado es técnicamente difícil de realizar y el resultado obtenido es realmente interesante. En este caso se afirma que se ha logrado un cristal de tiempo continuo porque la frecuencia de la biestabilidad depende de detalles no controlables de la configuración inicial de los átomos en la red óptica; así en diferentes repeticiones del experimento se observa que dicha frecuencia parece aleatoria (en un intervalo no muy grande entre 9 y 10.5 kHz). Esta es la razón por la que se llama cristal de tiempo continuo a este sistema, pues si fuera discreto dicha frecuencia estaría fijada a un subarmónico de la frecuencia de excitación. El artículo es Phatthamon Kongkhambut, Jim Skulte, …, Hans Keßler, «Observation of a continuous time crystal,» Science 377: 670-673 (09 Jun 2022), doi: https://doi.org/10.1126/science.abo3382, arXiv:2202.06980 [cond-mat.quant-gas] (14 Feb 2022); más información divulgativa en Lindsay J. Leblanc, «Unleashing spontaneity in a time crystal. Ordered patterns reoccur over time in an ultracold atomic gas trapped in light,» Science 377: 576-577 (04 Aug 2022), doi: https://doi.org/10.1126/science.add2015.

El experimento es difícil de realizar porque requiere un exquisito ajuste fino de todos los parámetros, lo que implica que el cristal de tiempo continuo logrado es poco robusto. No quiero entrar en los detalles; solo resaltaré que se usa la transición electrónica asociada a la línea D1 del ⁸⁷Rb (transición entre el estado fundamental y el primer estado excitado) que cae en el infrarrojo, a una longitud de onda de 794.98 nm; el láser de bombeo tiene que estar desplazado hacia el azul (menor longitud de onda) respecto a dicha línea en una cantidad justa, que determina la constante de red de la retícula óptica; en concreto, se usa una frecuencia de λP = 792.55 nm. Los parámetros del sistema se deben ajustar para que se observe la superradiancia de Dicke. El modelo de Dicke en óptica cuántica se describe la interacción entre la luz y los átomos asumiendo que la luz tiene un único modo en la cavidad óptica y que los átomos tienen dos niveles electrónicos. En dicho modelo se observa una transición de fase de segundo orden a un estado superradiante; en dicho estado los N átomos emiten luz coherente con una intensidad proporcional a N² (la superradiancia), en lugar de proporcional a N (como ocurre en el estado normal del modelo).
Por cierto, que la imagen que abre esta pieza no te engañe, no creas que cada átomo de rubidio se coloca en un mínimo o un máximo de la red óptica en la cavidad. Obviamente no es así, las dos configuraciones del cristal de tiempo corresponden a dos distribuciones de la densidad de los átomos en la red. En el artículo no indica de forma explícita el número de nodos (mínimos) y antinodos (máximos) de la retícula, pero deben ser unas pocas decenas, muchas menos que los ≈ 50 000 átomos de rubidio-87 del condensado.
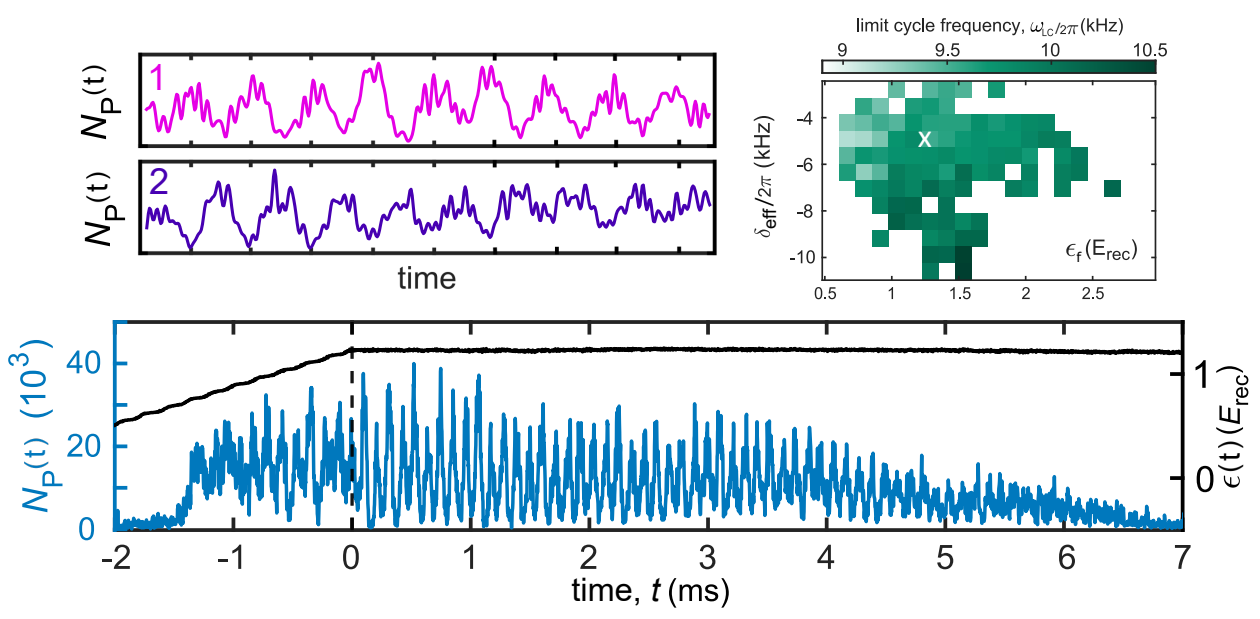
El punto clave es que el periodo de la oscilación biestable es aleatorio. Esta figura ilustra el comportamiento oscilatorio observado en el cristal de tiempo continuo. En la parte inferior se observa cómo fluctúan en el tiempo el número de átomos NP en los mínimos de la retícula óptica; dicho número funciona de forma cuasiperiódica, decreciendo en amplitud conforme avanza el tiempo (a los 7 ms ya quedan muy pocos átomos en la cavidad). En la parte superior izquierda se muestran 9 y 10 periodos de dos realizaciones (marcadas con 1 y 2) del experimento, mostrando que el periodo cambia de una realización a otra. Y en la parte superior derecha se observa cómo varía la frecuencia del cristal de tiempo entre diferentes realizaciones del experimento, entre ~9 kHz y ~10.5 kHz (colores verdes en el plano que muestra dos parámetros de la retícula en los que no entraré). La crítica más obvia a la denominación de cristal de tiempo continuo a este experimento es que la variación de la frecuencia de biestabilidad es muy limitada; por ello habrá que esperar a futuras realizaciones independientes que muestran un rango más amplio de frecuencias que no dejen lugar a dudas de que se trata de un cristal de tiempo continuo en lugar de uno discreto con un estado inicial perturbado de forma no controlada.
En resumen, se ha logrado observar un régimen de oscilación en una retícula de los átomos en un condensado de Bose–Einstein confinado dentro de una cavidad óptica. El comportamiento oscilatorio observado en este sistema abierto y, por tanto, disipativo se interpreta como un cristal de tiempo continuo. Siendo la primera realización física que se puede calificar con dicho nombre ha acabado publicado en Science. Sin embargo, hay que esperar a futuras implementaciones independientes para estar seguros de que realmente se ha implementado un cristal de tiempo continuo y que la comunidad científica lo acepte como tal. Sin lugar a dudas se trata de un resultado interesante, que podría tener aplicaciones en metrología cuántica, para la observación de propiedades de los BEC en cavidades. Habrá que estar al tanto de cómo responden a este trabajo sus competidores.


Entonces se puede hacer experimentos pompeando periódiamente donde el cristal de tiempo dependera de la frecuencia de forzamiento (como el que hizo Google el año pasado) y también se puede hacer experimentos pompeando continuamente donde el cristal dependera de la frecuencia a la que emite (como en este experimento)?
Y no entiendo bien porque el laser debe desplazarse de 794.98 nm (D1) a 792.55 nm ni porque el desplamiento esta determinado por la retícula óptica no debería esta influir solo en el desfase de la resonancia? Gracias y saludos
Dabed, no entiendo tu primera pregunta (quizás se refiere a la diferencia entre cristales de tiempo discretos y continuos). En cuando a la segunda, el punto clave es la superradiancia de Dicke. En la teoría de Dicke podría ocurrir tanto para un desafinado hacia el rojo (red-detuning) como para un desafinado hacia el azul (blue-detuning). Sin embargo, tras una intensa búsqueda experimental desde 2002, en el primer caso fue imposible observarla; pero cuando se buscó en el segundo caso, para sorpresa de muchos, se logró observarla en 2019. Por ello en este estudio se usa dicho caso.
Por otro lado, quizás me he explicado mal en la pieza, el desplazamiento no está determinado por la retícula óptica sino al revés, determina la distancia entre nodos en la retícula. Lo releo y lo cambio si no está claro. [No he cambiado nada, no encuentro qué frase puede inducir tu interpretación de mis palabras].
Sobre el blue tunning ya me queda más claro y sobre si el desplazamiento esta determinado por la retícula óptica o si viceversa, yo entendí mal y el texto esta perfecto. De hecho en otra parte donde escribes que la imagen no nos engañe, yo justamente me encontraba engañado hasta antes de leer esa parte, por lo que es una buena aclaración anticipando un error del lector.
Sobre la primera pregunta, solo quería confirmar que en el experimento de Google lo que importa no es la frequencia con que emite el laser pero si la frecuencia de forzamiento con la que se injecta periódicamente el laser al sistema mientras que en este experimento el laser se injecta continuamente por lo que importa no es la frequencia de forzamiento ya que no hay si no que la frequencia a la que emite el laser. Muchas gracias nuevamente.