En 2011 Allan H. MacDonald y Rafi Bistritzer introdujeron un modelo matemático para la estructura de bandas de moiré del grafeno bicapa rotado y acuñaron el término «ángulo mágico». En dicho modelo hay una secuencia infinita de ángulos mágicos (1.05°, 0.50°, 0.35°, 0.24°, 0.20°, …). He visto muy pocos artículos que discutan las diferencias en la estructura electrónica para los diferentes ángulos mágicos. Entre ellos me ha gustado un artículo en Physical Review B que usa una versión simplificada del modelo de MacDonald y Bistritzer, el llamado hamiltoniano quiral; este modelo usa matrices 2×2 en lugar de 4×4, lo que implica la ausencia de tunelado cuántico entre los sitios AA de la red de moiré. El modelo predice que el primer ángulo mágico es diferente del resto en cuanto a la relación (o equilibrio) entre las contribuciones positivas de la energía cinética y de la del potencial de confinamiento, y la negativa del operador de interacción intercapa. Seguramente, en el modelo de MacDonald y Bistritzer debe ocurrir algo muy parecido.
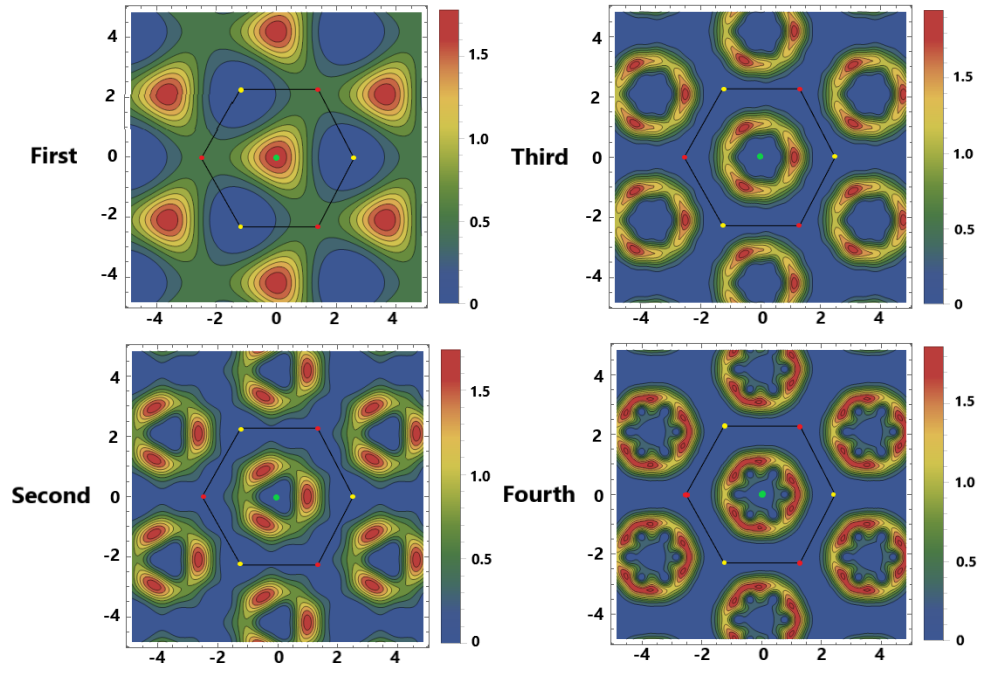
En el modelo del hamiltoniano quiral el origen de los ángulos mágicos está asociado a la frustración para la fase de las funciones de onda, que no puede llegar a π entre sitios diferentes. Los ángulos mágicos aparecen cuando la frustración es exactamente cero, con lo que los estados están altamente degenerados y aparece un salto de banda (bandgap) entre ellos y el resto del espectro. Me ha gustado especialmente esta figura que muestra la densidad electrónica en una de las capas de grafeno que presenta simetría rotacional C3 (hay una figura para en la otra capa pero muestra una simetría muy similar). Para el primer ángulo mágico la densidad presenta un máximo en los puntos AA; pero para los demás ángulos mágicos la densidad presenta varios máximos locales alrededor de los puntos AA, donde tiene un mínimo; así la densidad electrónica forma vórtices para los ángulos mágicos, salvo el primero. Estos vórtices se observan muy bien en la amplitud de los coeficientes de Fourier para ambas capas.
El modelo es sencillo; si te interesan los detalles disfrutarás con el artículo de Leonardo A. Navarro-Labastida, Abdiel Espinosa-Champo, …, Gerardo G. Naumis, «Why the first magic-angle is different from others in twisted graphene bilayers: Interlayer currents, kinetic and confinement energy, and wave-function localization,» Physical Review B 105:115434 (31 Mar 2022), doi: https://doi.org/10.1103/PhysRevB.105.115434, arXiv:2111.05957 [cond-mat.mes-hall] (10 Nov 2021); más sobre el modelo quiral en Gerardo G. Naumis, Leonardo A. Navarro-Labastida, …, Abdiel Espinosa-Champo, «Reduction of the twisted bilayer graphene chiral Hamiltonian into a 2×2 matrix operator and physical origin of flat bands at magic angles,» Physical Revew B 103: 245418 (14 Jun 2021), doi: https://doi.org/10.1103/PhysRevB.103.245418, arXiv:2102.09473 [cond-mat.mes-hall] (18 Feb 2021). El artículo con el modelo original es Rafi Bistritzer, Allan H. MacDonald, «Moiré bands in twisted double-layer graphene,» PNAS 108: 12233-12237 (26 July 2011), doi: https://doi.org/10.1073/pnas.1108174108, arXiv:1009.4203 [cond-mat.mes-hall] (21 Sep 2010).
Más información sobre el modelo de MacDonald y Bistrizer en la serie de seis artículos de B. Andrei Bernevig, Zhi-Da Song, …, Biao Lian, «Twisted bilayer graphene. I. Matrix elements, approximations, perturbation theory, and a k⋅p two-band model,» Physical Review B 103: 205411 (11 May 2021), doi: https://doi.org/10.1103/PhysRevB.103.205411, arXiv:2009.11301 [cond-mat.mes-hall] (23 Sep 2020 ); Zhi-Da Song, Biao Lian, …, and B. Andrei Bernevig, «Twisted bilayer graphene. II. Stable symmetry anomaly,» Physical Review B 103: 205412 (11 May 2021), doi: https://doi.org/10.1103/PhysRevB.103.205412, arXiv:2009.11872 [cond-mat.mes-hall] (24 Sep 2020); B. Andrei Bernevig, Zhi-Da Song, …, Biao Lian, «Twisted bilayer graphene. III. Interacting Hamiltonian and exact symmetries,» Physical Review B 103: 205413 (11 May 2021), doi: https://doi.org/10.1103/PhysRevB.103.205413, arXiv:2009.12376 [cond-mat.str-el] (25 Sep 2020); Biao Lian, …, Dmitri K. Efetov, …, B. Andrei Bernevig, «Twisted bilayer graphene. IV. Exact insulator ground states and phase diagram,» Physical Review B 103: 205414 (11 May 2021), doi: https://doi.org/10.1103/PhysRevB.103.205414, arXiv:2009.13530 [cond-mat.str-el] (28 Sep 2020); B. Andrei Bernevig, Biao Lian, …, and Zhi-Da Song, «Twisted bilayer graphene. V. Exact analytic many-body excitations in Coulomb Hamiltonians: Charge gap, Goldstone modes, and absence of Cooper pairing,» Physical Review B 103: 205415 (11 May 2021), doi: https://doi.org/10.1103/PhysRevB.103.205415, arXiv:2009.14200 [cond-mat.str-el] (29 Sep 2020); Fang Xie, Aditya Cowsik, …, Nicolas Regnault, «Twisted bilayer graphene. VI. An exact diagonalization study at nonzero integer filling,» Physical Review B 103: 205416 (11 May 2021), doi: https://doi.org/10.1103/PhysRevB.103.205416, arXiv:2010.00588 [cond-mat.str-el] (01 Oct 2020).

