
Aprender a columpiarse solo, sin ayuda, es todo un reto en los parques infantiles. Tras prueba y error acaban aprendiendo a ascender cada vez más alto. El columpio se comporta como un oscilador paramétrico formado por un péndulo (el columpio) y un sistema articulado formado por dos péndulos (el tronco y las piernas de la persona columpiante). La clave es mover la espalda hacia atrás mientras se levantan las piernas en el momento adecuado de la oscilación. Se publica en Physical Review E un análisis teórico (bidimensional) y experimental (con diez voluntarios) de la dinámica de este oscilador acoplado. Cuando se inicia el balanceo, lo más eficiente es echarse hacia atrás justo en el punto más bajo en el ciclo de subida hacia adelante; pero para alcanzar una altura aún mayor conviene cambiar la pauta y hacerlo en el ciclo de subida hacia atrás, justo antes de alcanzar la altura máxima. Esta predicción del modelo se ha confirmado con experimentos gracias a diez voluntarios (que aprendieron de niños estos movimientos).
Como siempre, este tipo de modelos matemáticos sencillos son ideales para que los profesores de física los usen en sus clases. Hoy en día, con cámaras de vídeo en todos los teléfonos móviles, se pueden realizar experimentos en cualquier parque infantil; los estudiantes podrán verificar su modelo mientras disfrutan de una clase al aire libre. Incluso, si algún estudiante nunca aprendió a columpiarse, se le pueden dar las instrucciones que se derivan del modelo para que aprenda. Como el estudio analítico de las ecuaciones y sus soluciones es engorroso, lo más conveniente es que los estudiantes usen métodos numéricos (fáciles de usar en Matlab, Mathematica, R, Python, o cualquier otro lenguaje de programación). Sin lugar a dudas será un ejercicio práctico con el que disfrutarán.
El artículo es Chiaki Hirata, Shun’ichi Kitahara, …, Michael J. Richardson, «Initial phase and frequency modulations of pumping a playground swing;» Physical Review E 107: 044203 (10 Apr 2023), doi: https://doi.org/10.1103/PhysRevE.107.044203; las ecuaciones usadas son similares a las de L. A. Klimina, A. M. Formalskii, «Three-Link Mechanism as a Model of a Person on a Swing,» Journal of Computer and Systems Sciences International 59: 728-744 (2020), doi: https://doi.org/10.1134/S1064230720050081; Paul Glendinning, «Adaptive resonance and pumping a swing,» European Journal of Physics 41: 025006 (2020), doi: https://doi.org/10.1088/1361-6404/ab6a63. Si algún profesor prefiere un modelo mucho más sencillo, le recomiendo Stephen M. Curry, «How children swing,» American Journal of Physics 44: 924-926 (1976), doi: https://doi.org/10.1119/1.10230; o en español, Carlos A. Perazzo, Julio Gratton, «El columpio,» Anales AFA 16: 9-12 (2004) [PDF]; y para un modelo intermedio, Sergiy Koshkin, Vojin Jovanovic, «Swinging a Playground Swing: Torque Controls for Inducing Sustained Oscillations,» IEEE Control Systems Magazine 42: 18-34 (April 2022), doi: https://doi.org/10.1109/MCS.2021.3139552. En este blog también puedes leer «El columpio argentino que se mueve solo y la mecánica de un columpio», LCMF, 09 ene 2008.

Para este tipo de modelos, la formulación lagrangiana es la más conveniente; en ella, basta determinar los diferentes grados de libertad con los que expresar las energías cinética y potencial. A este modelo le falta el término de fricción, que depende de la velocidad (cuya inclusión exige un lagrangiano generalizado, pero que en el artículo se incluye a mano en las ecuaciones de Euler–Lagrange). También le falta el término de forzamiento (el hecho de que el movimiento del tronco ϕ(t) y de las piernas ψ(t) es acompasado por la persona en este oscilador paramétrico). No entraré en más detalles del modelo, fáciles de entender para cualquiera con un mínimo de conocimientos de mecánica analítica.
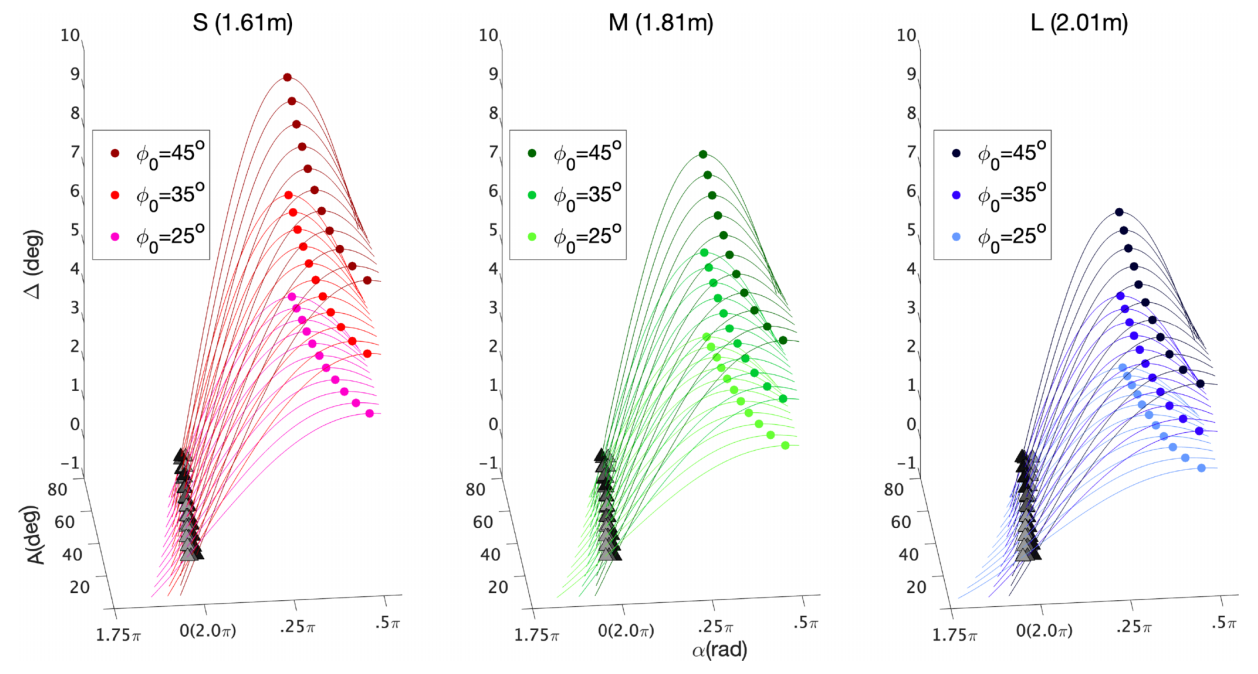
En los experimentos el asiento cuelga de un columpio con un altura de 2.29 m en una habitación con un techo de 3.00 m; se emplearon cadenas para el asiento con tres longitudes: 1.61 m para la corta (S), 1.81 m para la mediana (M) y 2.01 m para la larga (L). Las imágenes de los voluntarios se capturaron con cuatro cámaras (OQUS 300, Qualisys, Suecia). Esta figura muestra la ganancia Δ en amplitud en cada oscilación del columpio (en el artículo se presenta la fórmula matemática para el modelo sin fricción) para las tres longitudes de cadena del columpio estudiadas S, M y L.

Los resultados de los experimentos se muestran para 210, 226 y 260 oscilaciones de los participantes en los columpios S, M y L, resp. El ajuste lineal es pobre (R² = 0.57, 0.41, y 0.30 para S, M y L, resp.). Además, los valores de la ganancia Δ en amplitud por ciclo medido son mayores que los predichos por el modelo teórico sin fricción (se alejan más para S y M que para L). Por ello parece necesario incluir la fricción y la resistencia del aire, lo que requiere usar métodos numéricos para obtener la solución del modelo teórico.

El análisis de los vídeos permite reconstruir el periodo (en segundos) para la oscilación del asiento y del cuerpo, así como el ángulo de la espalda (en el movimiento de echarse hacia atrás). Los resultados para el periodo asiento se ajustan bien al modelo teórico; pero los resultados para el movimiento de la espalda tienen mucha dispersión (como es esperar, ya que lo voluntarios no son robots de Boston Dynamics).
En resumen, como suele ser habitual en este tipo de artículos de carácter educativo (aunque se haya publicado en Physical Review E en lugar de Physical Review Physics Education Research) son de mayor interés para los profesores de física que para el público en general. El modelo confirma lo que todo el mundo ha aprendido por experiencia propia; no hay sorpresas. Aunque quizás los más frikis aprovechen las conclusiones del modelo teórico para entrenarse con objeto de lograr la máxima altura en el columpio. Al fin y al cabo, la biomecánica se aplica en las ciencias del deporte para mejorar el rendimiento de los deportistas.


Hace algunos años, en el parque de Madrid Río, pusieron unos columpios que colgaban de uno de los puentes; estamos hablando de una cadena de muchos, muchos metros. Padres y niños intentábamos columpiarnos para llegar al cielo…pero era frustrante..; al autocolumpiarte hay un límite infranqueable debido a la largura de la cadena…es decir, mientras que con una cadena normal puedes llegar perfectamente a los 90 grados, acá te quedabas a lo sumo en 20 grados y siquiera con alguien que te empujara, colgándose del columpio si era necesario, llegabas ni de lejos a los 45 grados, lo cual ya hubiera sido flipante por la altura de las cadenas.
Mi experiencia es que con cadenas no puedes subir mucho por el peso de estas. Con sogas o cuerdas se alcanza mayores alturas sin demasiado problema.
A mi hija le ha costado mucho aprender. Quizás con el Langrangiano le resulta mejor. Saludos!