George Gamow decía en los 1960 que todas las matemáticas puras tenían aplicación en física, salvo la teoría de números y la topología. Hoy en día la topología está por doquier en física. En física de materiales tenemos fases topológicas, aislantes topológicos, superconductores topológicos y semimetales topológicos. Y hay aplicaciones en teoría cuántica de campos, como el efecto Aharonov–Bohm, los monopolos magnéticos o las anomalías gauge. Enumerar todas las aplicaciones de la topología a la física sería casi imposible.
La revista Nature Physics dedica un número especial a la topología en física, con énfasis en física de materiales. Puedes consultarlo en «Focus: Topological matter,» Nature Physics 12: 615-718 (Jul 2016) [link]. El primer artículo está firmado por un físico de la Universidad de Zaragoza, España, Manuel Asorey, «Space, matter and topology,» Nature Physics 12: 616–618 (30 Jun 2016), doi: 10.1038/nphys3800. La figura que abre esta entrada muestra un fibrado de Hopf e ilustra dicho artículo. Permíteme un resumen.
Las fases topológicas de la materia están caracterizadas por un parámetro de orden global, en lugar de los parámetros de orden locales que vía roturas espontáneas de simetrías caracterizan las fases que no son topológicas. Las fases topológicas de la materia emergen de la topología de la estructura de bandas del espectro de energía del material. Ciertas bandas no son equivalentes entre sí porque no se pueden deformar unas en otras mediante transformaciones continuas.
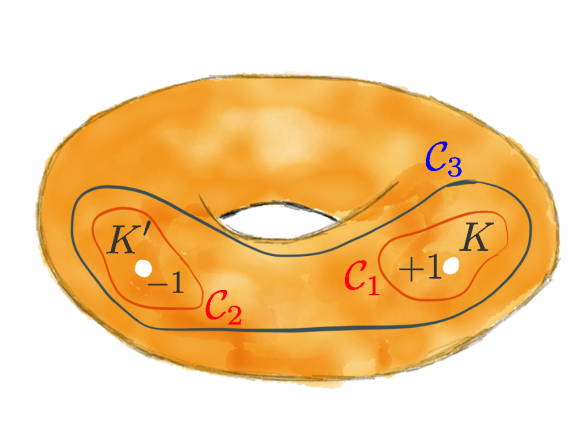
La topología se presenta en su esencia cuando consideramos las superficies y su número de agujeros. Hay una serie infinita de superficies (variedades diferenciables en dos dimensiones) que no son equivalentes topológicamente entre sí. La esfera S², el toro T²=S¹×S¹ (una esfera con un asa), el doble toro (una esfera con dos asas), y así sucesivamente.
En física también aparecen otros espacios de mayor dimensión con topología no trivial, como el grassmanniano Gr(m,n), que es el espacio de subespacios de dimensión m de un espacio vectorial complejo de dimensión n, sea ℂn con m ≤ n. El grassmanniano aparece en la clasificación de las fases topológicas de la materia porque Gr(m,n) está asociado con un sistema cuántico de n dimensiones con m niveles de energía ocupados.
La clasificación de los espacios topológicos con dimensión mayor de dos es un problema difícil. Se definen ciertos invariantes topológicos que discriminan las diferentes topologías. Por ejemplo, la clase de homotopía [X,Y] de una aplicación continua entre dos espacios X e Y. Este invariante topológico no puede ser modificado por una perturbación continua o diferenciable.
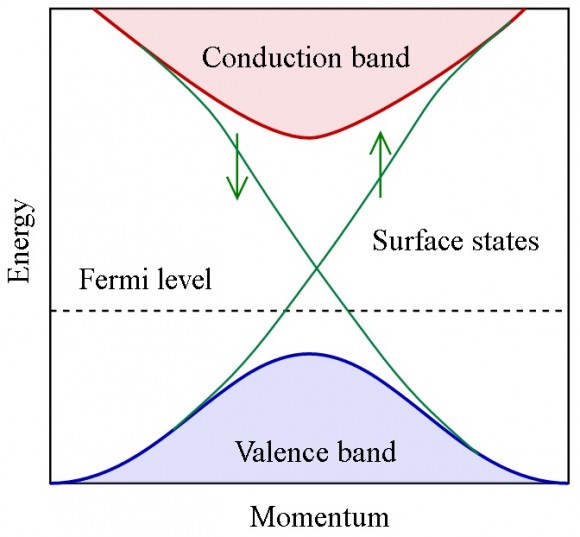
La conducción en los sólidos cristalinos se estudia mediante la teoría de bandas. La estructura periódica de la red de iones permite usar la teoría de Bloch para las funciones de onda periódicas de los electrones. Cada onda de Bloch está caracterizado por un momento k confinado en un región acotada llamada zona de Brillouin. Los materiales topológicos presentan una zona de Brillouin con una estructura topológica no trivial. Se asocia un fibrado a la zona de Brillouin, donde cada fibra corresponde al espacio de estados que tienen el mismo momento de Bloch k. Hay múltiples hamiltonianos H(k) que actúan sobre estas fibras para generar la estructura de bandas del espectro de energía. No importa la expresión concreta de dichos hamiltonianos, sino si perturbaciones en el sistema permiten deformar unos en otros. Los que están conectados de esta forma definen diferentes clases topológicas y dotan de robustez estructural a su correspondiente estructura de bandas.
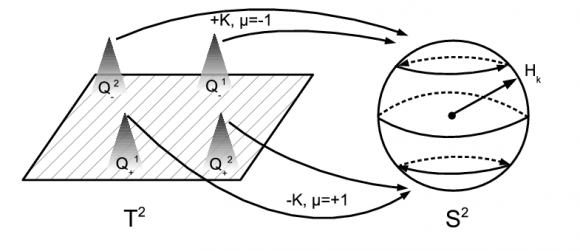
Por ejemplo, en un material que presenta el efecto Hall cuántico entero hay un número m (entero) de unidades de flujo de campo magnético a través de la celda unidad. La zona de Brillouin del material tiene las simetrías de un toro T². Para describir el efecto se asocia un fibrado E(T²) con m dimensiones a cada banda electrónica. Las clases del fibrado se clasifican mediante las clases de homotopía de las aplicaciones del toro T² sobre los grassmannianos Gr(m,m+n), con n>1, es decir, mediante la primera clase de Chern del fibrado. Para ν bandas rellenas dicho número entero es ν, siendo este número entero el responsable último de la cuantización del flujo en el efecto Hall cuántico entero.
La zona de Brillouin puede tener la simetría de una esfera S². El fibrado vectorial no trivial más sencillo en S² es el fibrado de Hopf (que ilustra la figura que abre esta entrada). Las fibras son vectores ℂ2 (dos números complejos) que representan el mismo estado cuántico en Gr(1,2) = S². El fibrado de Hopf tiene una única clase de Chern con ν = 1.
Los aislantes topológicos no sólo se pueden caracterizar mediante las propiedades topológicas de su espectro. También se pueden considerar las propiedades topológicas del espectro de sus estados en su contorno (edge states). Todo ello enriquece el número de posibilidades. Hay muchísimas fases de la materia que se caracterizan por diferentes propiedades topológicas. Este campo está en plena efervescencia. Espero que si te atreves, disfrutes con el especial de la revista Nature Physics dedicado a la topología en física [link].



Vengo del Futuro, y esto es el premio Nobel de Física 2016