El Modelo Estándar de las Partículas Elementales no explica ni la masa, ni la carga, ni la espín, de las partículas elementales conocidas, sino que impone dichos valores a partir de la evidencia experimental. En palabras de Feynman (traducidas) «Aún queda por resolver una característica muy poco satisfactoria (del Modelo Estándar): las masas de las partículas elementales observadas. No se conoce teoría que explique estos números. Los usamos en todos nuestros cálculos, pero no los entendemos (¿por qué tienen los valores que tienen? ¿de dónde vienen estos números?). En mi opinión (la de Feynman) este es uno de los problemas, desde el punto de vista fundamental (teórico), más serios e interesantes.»
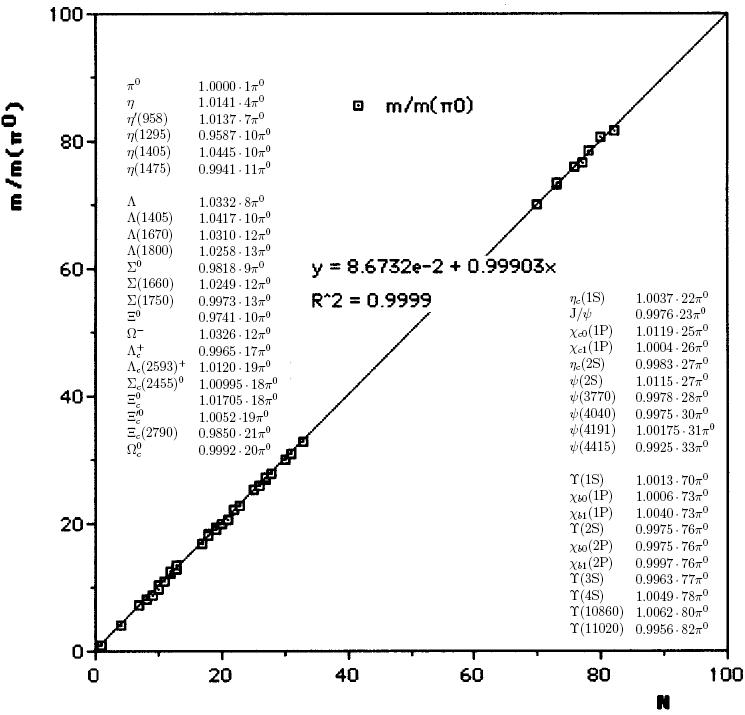
La figura de arriba, extraída de un artículo de E.L. Koschmieder, «Theory of the Elementary Particles,» ArXiv Preprint, 2008, que propone una «explicación», nos indica que la masa de los mesones (partículas formadas por un quark y un anti-quark) estables siguen un comportamiento lineal en función de la masa del mesón estable más ligero (el pión, partícula predicha por Yukawa). Esto ya se sabía de hace años… pero no había una explicación dentro del Modelo Estándar. Koschmieder trata de explicarla de forma no ortodoxa (numerológica) aludiendo a que refleja una teoría subyacente todavía desconocida. Este tipo de trabajos «numerológicos», normalmente tienen una capacidad predictiva «cuantitativa» muy limitada (dan aproximaciones burdas). Por ejemplo, en la «teoría» de Koschmieder la masa del neutrino electrónico (el más ligero de los 3 neutrinos conocidos) es igual a la masa del neutrino muónico (el segundo por masa) multiplicada por la constante de estructura fina (que indica la «fuerza» de la fuerza electromagnética entre partículas elementales). Como nadie conoce la masa de los neutrinos (se sabe que no es nula, pero no su valor, sólo la diferencia entre masas de los neutrinos se puede estimar teórica y experimentalmente sin una medida directa)… lo dicho, … como nadie la conoce, pues, por ahora, cualquier valor es «bueno».
La numerología es una de las «ramas» de la Física más denostada y criticada por todos los «científicos de pro». Aunque hay grandes físicos que han sido grandes defensores de la misma, como el propio P.A.M. Dirac o A.S. Eddington, la opinión estándar es relacionarla con el principio antrópico (defendido por «famosos» de la talla de S.W. Hawking) y concluir que de sus conclusiones aproximadas no se obtiene ciencia «verdadera». De todas formas, recordad la importancia que tuvo darse cuenta de que el protón y el neutrón (aparentemente tan distintos) eran la «misma» cosa (hoy en día, le llamamos nucleón), que introdujo el espín isotópico y con él gran parte de la moderna teoría cuántica de campos aplicada a partículas elementales (sustento del Modelo Estándar).
En esta línea, acaba de aparecer el artículo de T. A. Mir, G. N. Shah, «Order in the mass spectrum of elementary particles,» ArXiv preprint, que propone explicar la figura de arriba usando como parámetro la diferencia de masa entre el pión (hadrón tipo mesón) y el muón (leptón, tipo de electrón de mayor masa). Este nuevo artículo alude a que dicha diferencia (29.318 MeV) es una «unidad fundamental» de masa. De curiosidades «numerológicas», la vida está llena.
La numerología siempre me recuerda a la famosa «estética» de la proporción del número phi o número dorado o número mágico o phi = (1+raizcuadrada(5))/2 y a la aparición de los números de Fibonacci en biología. Cuando lees ciertas páginas web y artículos de divulgación parece que es completamente «verdad» que estos números aparecen por doquier (verdad numerológica). ¿Realmente aparecen los números de Fibonacci en la distribución de pétalos en las flores? Dedicaremos uan futura entrada de este blog a este «peliagudo» tema. Sólo quiero adelantar, que científicamente no es así. Hay flores de ciertas especies de plantas que sí siguen una distribución de este tipo, pero la gran mayoría no. Estadísticamente, es mera casualidad. Pero y lo que bonito que queda deshojar («despetalear») una margarita (que sí, que no, que sí, que no, …) si uno no sabe cuántos pétalos tiene. De la especia más común en España, hay flores con n (no digo cuántos ni si es par o impar) pétalos, pero que excepcionalmente también presentan n+1 o n-1 pétalos (con menor probabilidad pero nada despreciable). ¿Tienes alguna margarita a mano?
Para saber más (todo un clásico): G. J. Mitchison, «Phyllotaxis and the Fibonacci Series,» Science, 196: 270-275, 15 April 1977. Y un libro curioso, Mario Livio, «The Golden Ratio. The Story of Phi, the World’s Most Astonishing Number,Broadway Books, New York, 2002, que está traducido al español «La proporción aúrea,» 3ra. ed., Ariel, 2006.


El Instituto Clay ofrece 1.000.000 de dolares a quien explique el «mass gap», que tendría que coincidir con una respuesta a la pregunta que se presenta en esta entrada.
Soy licenciado en ciencias físicas. Incluso llegué a estudiar un curso de Física teórica (mecánica cuántica etc.) pero todo eso ya me queda muy lejos pues estoy jubilado.
He llegado a esta página:
¿Se puede predecir la masa de las partículas elementales? (o un poco más de Numerología, por favor)
buscando un artículo que leí hace años en la wikipedia sobre un físico alemán (ya fallecido) que tenía una teoría no ortodoxa sobre las partículas elementales, que predecía con cierta precisión la masa de algunas de ellas.
Su teoría es casi desconocida porque no la publicó en inglés, solo en alemán y se tardó mucho en traducirla.
He intentado volver a dicha página web pero no la encuentro. No sé si la he perdido con una destrucción que he tenido de mi disco duro.
No sé si usted sabe algo de esto y podría ayudarme a encontarla.
Un saludo.
Roberto, supongo que te refieres a la fórmula de masa de Burkhard Heim (1925-2001) [wikipedia].
Heim’s Mass Formula (1982), Heim’s Mass Formula (1989) y Mass Tables.