Ya puedes escuchar mi nuevo podcast para Trending Ciencia del 9 de diciembre de 2013 (el podcast dice 8 porque fue grabado ayer). Este podcast es la segunda parte de mi podcast de la semana pasada, que estaba basado en el artículo de Art Hobson (Universidad de Arkansas, Fayetteville, Arkansas, EEUU), “There are no particles, there are only fields,” (“No hay partículas, sólo hay campos”), American Journal of Physics 81: 211, 2013 (arXiv:1204.4616 [physics.hist-ph]). Como ya dije el universo está hecho de campos cuánticos, el objeto que estudia la mecánica cuántica relativista, que permiten entender todas las paradojas de la mecánica cuántica no relativista desde un foco muy diferente, permíteme profundizar un poco más en estas ideas.
En mecánica cuántica no relativista la noción de partícula entra en conflicto con la causalidad y la localidad descritas por la teoría de la relatividad de Einstein. Por lo tanto, en principio, la mecánica cuántica no relativista permite la transmisión de señales a una velocidad mayor que la velocidad de la luz en el vacío y la violación del principio de causalidad (que la causa precede al efecto), lo que puede provocar múltiples paradojas. En la práctica, todos los protocolos cuánticos de transmisión de información requieren el envío por un canal clásico del resultado de ciertas medidas cuánticas y este canal clásico cumple las leyes de la relatividad prohibiendo la propagación superlumínica de señales cuánticas. Esto pone a salvo todos los protocolos cuánticos conocidos, que se pueden usar para enviar información, y todos ellos cumplen la teoría de la relatividad de forma indirecta, no pudiendo violar la causalidad. Sin embargo, hay una cosa muy importante que debemos recordar, que hasta ahora no se conozca ningún protocolo cuántico no significa que se pueda demostrar matemáticamente que dicho protocolo no exista. En el marco de la mecánica cuántica no relativista es imposible demostrar de forma rigurosa que no exista dicho protocolo. La razón es obvia, la mecánica cuántica no relativista no incluye de forma explícita la velocidad de la luz en el vacío, ni ningún límite físico que impida la existencia de velocidades infinitamente grandes.
La única manera rigurosa de demostrar que la mecánica cuántica no viola la relatividad es utilizar la mecánica cuántica relativista, es decir, la teoría cuántica de campos. El resultado más famoso es el teorema de Phillippe H. Eberhard y Ronald R. Ross de 1989 («Quantum field theory cannot provide faster-than-light communication,» Foundations of Physics Letters 2: 127-149, 1989). Su demostración utiliza argumentos muy generales que no requieren la invarianza Lorentz explícita de las ecuaciones, basta que los operadores en regiones separadas por una distancia espacial (fuera de sus respectivos conos de luz) conmuten (para campos bosónicos) o anticonmuten (para campos fermiónicos). Sus argumentos son fáciles de entender y demuestran que la teoría cuántica de campos no permite la comunicación utilizando señales más veloces que la luz en el vacío. Como la mecánica cuántica no relativista es una aproximación a la teoría cuántica de campos, toda violación de esta propiedad se encuentra fuera de los límites de validez de dicha teoría.
Otra característica de la mecánica cuántica no relativista es la imposibilidad de localizar una partícula en cierta región finita o acotada del espacio, el llamado teorema o paradoja de Gerhard C. Hegerfeldt de 1974 («Remark on causality and particle localization,» Physical Review D 10: 3320-3321, 1974). La ecuación de Schrödinger dependiente del tiempo es una ecuación lineal que no tiene soluciones de soporte compacto, cuando el potencial es una función regular (es decir, suficientemente diferenciable). Que la función de onda no puede ser exactamente cero en el exterior de una región dada del espacio, se interpreta en física como que es imposible localizar una partícula en dicha región del espacio, siempre hay una probabilidad distinta de cero de que se encuentre fuera de dicha región. Incluso si forzamos que así ocurra en un momento dado, con una condición inicial de la ecuación de Schrödinger que sea una función de onda de soporte compacto, su evolución en tiempo hace que un instante infinitesimal más tarde la solución sea distinta de cero en todo punto (aunque su valor decrece muy rápido con la distancia).
El teorema de Hegerfeldt tiene su origen en que la ecuación de Schrödinger no es una ecuación relativista y por tanto la función de onda no es local en el sentido relativista del término. Por ello la función de onda cuántica puede cambiar de valor de forma instantánea, algo que está prohibido por la teoría de la relatividad. El teorema de Hegerfeldt permite, en teoría, la propagación de señales a mayor velocidad que la luz en el vacío, pero como viola los principios de la teoría cuántica de campos es imposible de verificar esto de forma experimental. Los argumentos de la demostración de Eberhard y Ross permiten encontrar la «trampa» de la demostración del teorema de Hegerfeldt.
Una de las lectoras de mi blog, Valeria, preguntaba por una definición sencilla e intuitiva del concepto de campo. Yo le contesté que no hay ninguna, los conceptos fundamentales son conceptos axiomáticos, permiten construir conceptos derivados, pero no pueden ser definidos con conceptos más fundamentales (pues entonces no lo serían ellos mismos). Conceptos fundamentales como qué es el tiempo, qué es el espacio, o incluso qué es la energía, no tienen definición (basada en conceptos más fundamentales) en la física actual. Todos estos conceptos tienen una formulación matemática rigurosa que permite usarlos en nuestras teorías para realizar predicciones que luego son confirmadas mediante experimentos. El físico, tras años de estudio, se acostumbra a trabajar con estos conceptos y cree que son intuitivos, pero en realidad no sabemos lo que son. Lo mismo le pasa al concepto de campo cuántico. Se requieren conceptos más fundamentales para explicar que son los campos cuánticos, conceptos que aún no tenemos.
Por supuesto, que nadie se equivoque. Los físicos tenemos una definición matemática rigurosa del concepto de teoría cuántica de campos basada en cierto conjunto de axiomas. De hecho, hay varios conjuntos de axiomas posibles, que hasta donde se sabe son equivalentes entre sí. La teoría cuántica de campos axiomática más conocida es la de Arthur S. Wightman, desarrollada entre 1956 y 1964, pero también es muy conocida la teoría cuántica de campos algebraica de Rudolf Haag y Daniel Kastler en 1964, y la de integrales de camino euclidianas de Konrad Osterwalder y Robert Schrader de 1973. El concepto matemático de campo cuántico no tiene una descripción intuitiva sencilla y cualquier imagen que nos hagamos a partir del concepto de campo clásico es completamente equivocada. La formalización matemática rigurosa es importante para demostrar teoremas, como el teorema de la relación entre el espín y la estadística, o el teorema de invarianza CPT. Además, esta formalización es rigurosa para campos cuánticos escalares (como el bosón de Higgs) y campos gauge abelianos (como el electromagnetismo), pero aún no sabemos si permiten explicar los campos gauge no abelianos (como los que describen la interacción débil o la interacción fuerte). De hecho, el problema del milenio del Instituto Clay de Matemáticas sobre el salto de masa en las teorías de Yang-Mills requiere como primer paso una formalización axiomática rigurosa de los campos de Yang-Mills, que aún no conocemos. Pero no hay que tener falsas esperanzas, es muy posible que dicha axiomatización permita resolver problemas, pero es muy difícil que nos ayude a intuir lo que son los campos cuánticos, como ya ocurre con las axiomáticas de Wightman, Haag-Kastler y Osterwalder-Schrader.
Muchos oyentes pueden estar tentados a pensar que la teoría cuántica de campos se comporta como una teoría de variables ocultas para la mecánica cuántica no relativista. Nada más alejado de la realidad. La mecánica cuántica no relativista viola las desigualdades de Bell, el llamado teorema de Bell. Este teorema demuestra que no existe una teoría realista local subyacente a la mecánica cuántica, es decir, que no existe una teoría de variables ocultas. Usando la formulación axiomática de la teoría cuántica de campos se puede demostrar que también viola las desigualdades de Bell, más aún, además las viola de forma máxima, como demostraron Stephen J. Summers y Reinhard Werner en 1987 («Bell’s Inequalities and Quantum Field Theory. I. General Setting,» Journal of Mathematical Physics 28: 2440-2447, 1987; «Bell’s Inequalities and Quantum Field Theory. II. Bell’s Inequalities are Maximally Violated,» Journal of Mathematical Physics 28: 2448-2456, 1987; «Maximal Violation of Bell’s Inequalities is Generic in Quantum Field Theory,» Communications in Mathematical Physics 110: 247-259, 1987). En sentido estricto se puede afirmar sin rubor que la mecánica cuántica no relativista viola las desigualdades de Bell porque es una aproximación a la teoría cuántica de campos que también las viola. Que históricamente se descubriera antes lo primero, no implica que lo segundo no sea más fundamental.
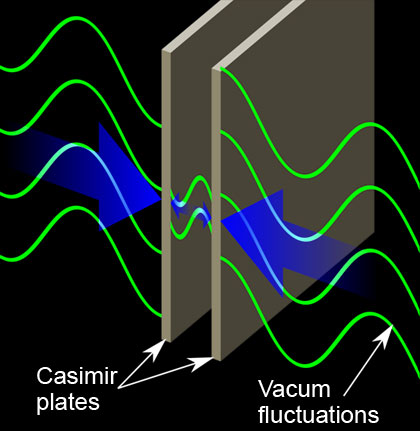
El lector se preguntará si es posible explorar de forma experimental los campos sin recurrir al concepto de partícula y la respuesta es que sí se puede. El concepto de campo nos permite entender además del concepto de partícula, el concepto de partícula virtual, el concepto de vacío y el concepto de interacciones fundamentales. En concreto, el concepto de vacío de un campo cuántico ha sido explorado de forma indirecta gracias al efecto o desplazamiento de Lamb, descubierto por Willis Lamb en 1947, y gracias al efecto de Casimir, propuesto por Hendrik B. G. Casimir y Dirk Polder en 1947 y medido por primera vez en 1972. También se han propuesto otros fenómenos, como el efecto de Unruh, propuesto por Stephen Fulling en 1973, Paul Davies en 1975 y William G. Unruh en 1976, pero que todavía no ha sido verificado en los experimentos (aunque se han interpretado ciertos fenómenos aún sin explicación como resultado del efecto Unruh, la mayoría de los expertos son escépticos al respecto).
El vacío de un campo cuántico es difícil de entender y de imaginar. Utilizando la versión perturbativa de la teoría cuántica de campos descrita mediante diagramas de Feynman, el vacío cuántico se representa como un mar de partículas virtuales que aparecen y desaparecen a pares gracias al principio de indeterminación de Heisenberg para el producto de la duración de un proceso cuántico y la variación de energía en dicho proceso. Sin embargo, no debemos engañarnos, las partícula virtuales no son partículas. La noción de partícula virtual refleja una descripción matemática perturbativa (es decir, aproximada) de las fluctuaciones o excitaciones del vacío del campo. La imagen de que las interacciones entre partículas está mediada por el intercambio de partículas virtuales es sólo una metáfora y no tiene nada que ver con la realidad. Esta metáfora tiene su origen en la belleza de los diagramas de Feynman y muchos físicos hemos abusado de ella porque pensábamos que permitía entender algo tan complicado como la interacción entre campos.
En mi blog he discutido en varias ocasiones (p.ej. «Qué es un electrón en teoría cuántica de campos» y «Los conceptos de campo, partícula, partícula virtual y vacío«) el concepto de partícula virtual, que la mayoría de los físicos preferimos llamar «partículas off-shell» (porque violan la ecuación de Einstein E=mc², que escribimos como E²=(mc²)²+(pc)², donde m es la masa de las partículas del campo, E es la energía contenida en la fluctuación y p es el momento lineal (en física newtoniana es la masa por la velocidad) que cumplen las partículas, también llamadas «partículas on-shell»). Se llama «partícula» a las partículas virtuales porque aunque no son partículas su interacción con partículas (o con campos) puede transformarlas en partículas (pueden pasar de ser fluctuaciones off-shell a fluctuaciones on-shell, es decir, pueden pasar de no cumplir la ecuación de Einstein a cumplirla). El término «virtual» se refiere a que las fluctuaciones off-shell no son observables de forma directa (se puede detectar una partícula, pero no una partícula virtual). En mi opinión, la imagen de que las fluctuaciones del vacío son un mar de partículas off-shell o virtuales genera más dificultades conceptuales a la hora de entender qué es el vacío cuántico de las que resuelve, pero repito que muchos físicos abusan de ella porque opinan lo contrario.





Perdona, Antonio, pero yo no mencioné a Zeh en mi anterior entrada. Quizás haya una tercera entrada…
Este paper de Hobson pretende poner un poco de orden en todo el enorme embrollo que supone la interpretación del «extraño mundo cuántico». Lo que Hobson pone de manifiesto es algo que todos los Físicos saben (supongo) pero que nadie se ha molestado en aclarar en todos los libros de texto sobre mecanica cuántica: los datos experimentales se pueden explicar en términos de campos cuánticos y sus excitaciones pero NO SE PUEDEN EXPLICAR en términos de partículas por lo tanto las entidades físicas fundamentales son los CAMPOS no las partículas.
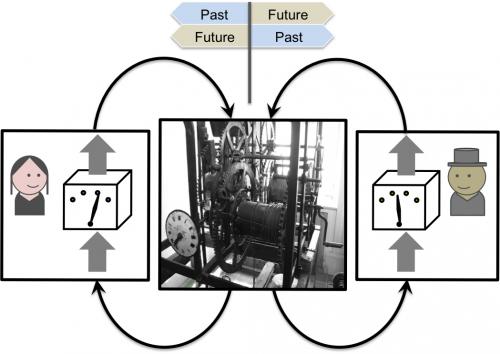
Los campos cuánticos se pueden considerar como una propiedad del propio espacio que constituye una entidad compacta que se extiende por todo el Universo, las excitaciones de dichos campos son lo que entendemos como partículas y son estas excitaciones las que «vemos» desplazarse por el espacio a una velocidad máxima de c. Este concepto de entidades extensas no localizadas permite resolver muchas de las paradojas de la MC. En el experimento de la doble rendija, el campo electrónico o el campo electromagnético se extiende a lo largo de todo el camino a recorrer, la fuente emisora NO CREA un nuevo campo sino que perturba el campo YA EXISTENTE produciendo una excitación que se desplaza siguiendo los criterios de la Relatividad, por esto el campo ya «tiene información» de todo el trayecto, ya «sabe» si la rendija está abierta o no y por supuesto, la perturbación pasa por ambas rendijas ya que el campo es un objeto extenso. En cada punto del espacio hay una probabilidad de detectar la PERTURBACIÓN del campo, la energía de la excitación del campo (la partícula) interacciona con las moléculas del detector o de la pantalla con cierta probabilidad y la energía detectada siempre es un múltiplo de hf, ya que la energía del campo es discontinua. Solo en términos de campos puede entenderse el vacío cuántico: en este no hay partículas, solo existe el campo en su estado mínimo de energía. La explicación en términos de partículas virtuales conduce a muchas paradojas. La oscilación cuántica y el mecanismo de Higgs son entendibles también en forma de campos, no olvidemos que el SM, que constituye uno de los más grandes logros de la ciencia es una teoría de campos.
Otro fenómeno que no menciona el articulo y que creo que se explicaría muy bien en términos de campos sería el entrelazamiento cuántico: los fotones entrelazados son la misma perturbación del campo que se desplaza en direcciones opuestas por lo que al medir una excitación se encuentra una correlación en la otra (por ejemplo spines opuestos).
La resolución de las paradojas tiene el precio de asumir la existencia de entidades físicas que permean todo el espacio, por supuesto estas entidades cuánticas no tienen nada que ver con el éter y sus cualidades «mecánicas». Sin embargo, si pensamos que el espacio, sea lo que sea, tiene que ser algo físico, es decir, provisto de energía (algo que puede curvarse cuando hay más energía próxima) y que esta energía está constituida por los campos cuánticos entonces éstos parecen más fáciles de asimilar. Al final la última frontera que nos conducirá a una teoría cuántica de la gravedad será precisamente entender la naturaleza del espacio-tiempo.
«Los fotones entrelazados son la misma perturbación del campo». Pueden serlo, y eso justifica una correlación, el problema es que en el test de Bell había un factor aleatorio en cuanto a la dirección de medida del spin, y si los dos spines eran «siempre» opuestos, a pesar del factor aleatorio, no parece que se pueda explicar sin la opción de que hay algo en el spin que se propaga por el campo más rápido de los que se propaga la luz.
Si alguien puede justificar que los campos no violan el límite de la velocidad de la luz, me gustaría saber cómo. Y por otra parte, si nada puede ser más veloz que la luz, ¿por qué se acepta que la expansión del espacio-tiempo sí puede serlo?
Un análisis frecuencial de este texto (que sería una forma limitada de analizarlo, lo acepto) pero muestra que aparece 8 veces palabras que contienen «axioma», es demasiado para provenir de la física.
¿Si dejamos eso a los matemáticos que lo vienen estudiando bien y saben sus limitaciones?. Creer que usar esa palabra beneficia a la física y la hace «rigurosa» (palabra que aparece 7 veces), no aporta mucho. Se parece a los que hacen pseudociencia y usan la palabra Energía en cualquier lado.
La física puede cambiar, no tiene axiomas, todo está sujeto a darse vueltas pata para arriba, física no es matemática, es lamentable que no se comprenda eso.
«La Física es a las Matemáticas lo que el ..» (pueden buscar la cita de Feynman)
¿Por qué tu física parece siempre hecha con palos y con piedras? Serías un genio si hubieras nacido con el telégrafo.
Estimado Don Francis,
Son chileno, y junto con saludarlo y manifestarle mi admiración y respeto por su brillante labor como científico y divulgador, quería preguntarle qué ocurrió con su página antigua, que era mucho más completa que la actual. ¿quizás existe ahora con otro nombre?
Agradeceré sus comentarios
Carlos, la antigua está redirigida a esta. Todo lo que había en la antigua se encuentra en esta otra (salvo contadas excepciones).