Una tortuga con un caparazón más grande parece más protegida, salvo cuando cae de espaldas y no puede darse la vuelta. La geometría del caparazón determina la estrategia que debe usar la tortura para darse la vuelta. Un análisis biomecánico ha determinado tres posibles puntos de equilibrio que determinan la cantidad de energía biomecánica para realizar el giro. Las tortugas planas usan sobre todo el empuje del cuello. Las tortugas muy abombadas y de cuello corto oscilan hasta apoyar las patas en el suelo y empujar con ellas. Las tortugas intermedias combinan ambas estrategias.

La noticia «Big tortoise shell makes flipping hell,» Nature 520: 8, 02 Apr 2015, doi: 10.1038/520008c, sobre el artículo de Golubović Ana, Tomović Ljiljana, Ivanović Ana, «Geometry of self righting: the case of Hermann’s tortoises,» Zoologischer Anzeiger – A Journal of Comparative Zoology 254, 99-105, Jan 2015, doi: 10.1016/j.jcz.2014.12.003, me llevó al artículo de Gábor Domokos, Péter L Várkonyi, «Geometry and self-righting of turtles,» Proceedings B (Biological sciences) of The Royal Society 275: 1630, 07 Jan 2008, doi: 10.1098/rspb.2007.1188.

En apariencia el problema es sencillo (permíteme resumir el análisis de Domokos y Várkonyi en 2008). La geometría de una tortuga es más plana en su parte ventral (plastrón) que la parte dorsal (caparazón), con lo que la postura normal es más estable que la postura patas arriba. Dicha diferencia en estabilidad ayuda a minimizar la energía biomecánica necesaria para darse la vuelta. Problema resuelto. Sin embargo, muchas tortugas no son completamente planas en su parte ventral y su geometría transversal tiene dos puntos de equilibrio estable, uno de ellos en posición patas arriba. Un gran problema para estas tortugas. Aunque por fortuna para ellas su cuerpo es tridimensional, lo que introduce puntos de equilibrio inestables adicionales que ayudan a minimizar los esfuerzos biomecánicos necesarios.

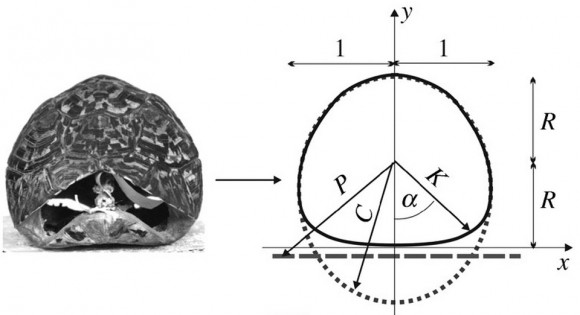
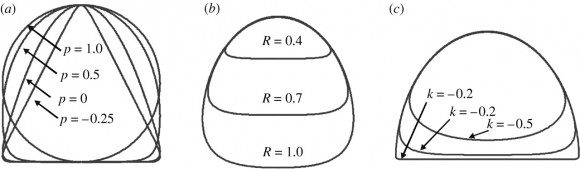
Para estudiar con un modelo matemático los puntos de equilibrio del cuerpo de una tortuga hay que usar un modelo geométrico simplificado del caparazón. Se puede usar tres parámetros básicos. El parámetro p determina la forma del caparazón, el parámetro R las posiciones relativas entre el caparazón y el plastrón, y el parámetro k la redondez en la transición entre el caparazón y el plastrón. Esta figura ilustra valores representativos de estos parámetros. Además de identificar la posición de los puntos de equilibrio, también hay que determinar su estabilidad (si son estables o inestables).

Como el análisis con tres parámetros geométricos es complicado. Se aprovecha que hay ciertas relaciones típicas entre dichos parámetros para estimar funciones aproximadas k(R) y p(R) que relacionan los parámetros k y p con los valores de R. Simplificar la geometría tiene sus ventajas, pero también sus inconvenientes (ya que la geometría de los caparazones de los quelonios es muy diversa). El análisis matemático identifica tres puntos de equilibrio S1, S2 y S3 que se pueden caracterizar usando el parámetro R. Gracias a ello la inmensa mayoría de las tortugas se puede clasificar en función de su parámetro R en tortugas con punto de equilibrio S1 (tortugas altas y abombadas), S2 (tortugas planas y delgadas) y S3 (tortugas intermedias).

Las tortugas planas con un valor bajo de R<0,6 (tipo S2) suelen usar el cuello para darse la vuelta. Estas fotografías lo ilustran con la tortuga Hydromedusa tectifera. El punto de equilibrio S2 es muy estable y hay que superar una gran barrera energética para lograr el giro. Por ello estas tortugas usan un empujón fuerte con el cuello que produce un momento de giro capaz de superar esta barrera de energía. La mayoría de las tortugas acuáticas y semiacuáticas siguen esta estrategia (familias Pleurodira, Chelydridae, Kinosternidae, entre otras).

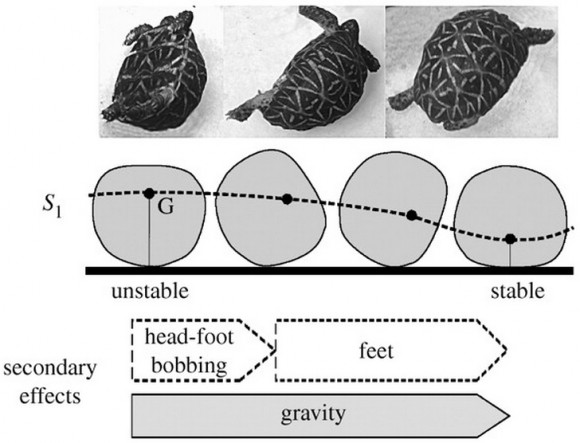
Las tortugas muy abovedadas con un valor alto de R > 0,8 (tipo S1) suelen usar movimientos oscilatorios hacia un lado y hacia otro meneando su cabeza y sus pies. Esta figura ilustra la tortuga Geochelone elegans. La barrera energética asociada a la estabilidad del punto S1 es pequeña, por lo que la energía biomecánica necesaria para el giro también es pequeña y un bamboleo permite lograr que alguno de los pies toque tierra; un empujón adicional con un pie, ayudado de la fricción con el suelo, produce la energía biomecánica necesaria para lograr el giro. Esta estrategia es seguida por la mayoría de las tortugas terrestres, con caparazones muy abovedados y cuellos cortos (familias Geochelone, Stigmochelys, Astrochelys y algunas especies de Terrapene y Testudo).

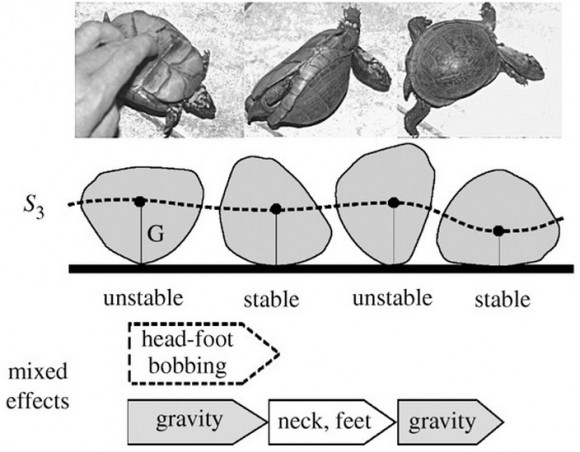
Las tortugas intermedias con valores 0,6 < R <0,8 (tipo S3), como la Terrapene carolina de la fotografía, usan una combinación de las dos estrategias anteriores, un empuje con el cuello y con las patas apoyándose en el suelo. Muchas tortugas de las especies Testudo y Terrapene, y de la familia Psammobates usan esta estrategia.

Por cierto, el artículo de Ana Golubović et al., citado en Nature, estudia la tortuga mediterránea (Testudo hermanni), tortuga de tipo S3, que en España podemos encontrar en libertad en Cataluña y en las Islas Baleares. Estas tortugas están incluidas en la Lista Roja del IUCN de especies amenazadas de extinción y está absolutamente prohibida la captura de ejemplares salvajes. Han estudiado en el campo 118 quelonios (54 hembras y 64 machos) recogidos en las exrepúblicas yoguslavas (Macedonia, Montenegro y Serbia). Se realizaron un total de 452 intentos de giro con las 118 tortugas puestas patas arriba sobre la misma superficie horizontal. Todos se realizaron in situ y tras la tortura de los experimentos fueron dejadas en libertad.

Las hembras de las tortugas del mediterráneo suelen ser más grandes que los machos. Durante la época de apareamiento, los combates entre machos rivales provocan que muchos acaben dándose la vuelta. Los machos deben ser capaces de retornar a su posición normal lo más rápido posible. Por ello se trata de un quelonio ideal para estudiar cómo se la vuelta una tortuga terrestre (aunque la mayoría son tipo S3). Todas las tortugas fueron medidas y luego dadas la vuelta sobre una superficie horizontal plana para ver cómo se giraban (no todas lo lograron en menos de ocho minutos, tiempo máximo de tortura). Ana Golubović et al. compararon la morfometría geométrica (índices geométricos asociados a la forma del caparazón) con el tiempo necesario para darse la vuelta.

Se cree que los machos son más pequeños que las hembras para favorecer una mayor movilidad y poder localizar más fácilmente a las hembras con las que aparearse con éxito. En los combates entre machos, un mayor tamaño implica poder inmovilizar al competidor, pero un menor tamaño implica mayor movilidad y agilidad para darse la vuelta. Por ello la selección sexual ha dado lugar a un dimorfismo sexual. Esta figura ilustra los resultados obtenidos (cuadrados para hembras y círculos para machos; símbolos rellenos en negro para los ejemplares incapaces de darse la vuelta, la mayoría hembras). Para mí lo más curioso del estudio es observar la gran variabilidad del parámetro R entre ejemplares de la misma especie. Algo que los naturalistas y biólogos considerarán obvio.

Sin entrar en más detalles, sorprende que un modelo matemático sencillo con un sólo parámetro morfogeométrico permita caracterizar las estrategias que usan las tortugas para darse la vuelta. Por supuesto, modelos más precisos podrán afinar los detalles. Pero no quita que en la sencillez esté la virtud.