Para explicar bien la teoría de cuerdas hay que usar conceptos matemáticos abstractos, lo que requiere un lector con cierta preparación matemática. Entre los libros sin fórmulas matemáticas, me veo obligado a reseñar Andrew Zimmerman Jones (con Daniel Robbins), «String Theory For Dummies,» Wiley (2010) [384 pp.] (web del libro). Andrew es un divulgador científico que no posee el título de Ciencias Físicas, por ello ha sido asesorado por un doctor en física, Daniel Robbins. Su libro está bien escrito, pero hay muchas cosas que no me gustan.
Como el libro de George Musser [reseña LCMF] está dirigido a legos sin conocimiento previo sobre la teoría, por lo que muchos de vosotros pensaréis que es un libro demasiado básico. Se diferencia del Musser en que discute las guerras cuerdísticas (string wars) y su muestra escéptico sobre el futuro de la teoría. Lo que más echo en falta es que habla muy poco de branas y teoría M (menos del 5% del libro). Aún así, para muchos aficionados a la divulgación científica el libro de Zimmerman Jones, que tiene una reputada experiencia como divulgador de física para The New York Times, será una lectura bastante recomendable.
[youtube=https://www.youtube.com/watch?t=117&v=y0UcrGncBTo]
El libro está dividido en seis partes. La parte 1 introduce la idea de la teoría de cuerdas como teoría de todo y como teoría cuántica de la gravedad. La parte 2 introduce toda la física prerrequisito a la teoría de cuerdas. La parte 3 ofrece un resumen breve de la teoría de cuerdas, incluyendo un poco de teoría M. La parte 4 se adentra en las dimensiones extra, el multiverso y los viajes en el tiempo. La parte 5 discute (con la boca grande) las alternativas a la teoría de cuerdas. La última parte presenta algunas predicciones (sesgadas hacia lo negativo) sobre el futuro de la teoría y nos presenta a diez físicos famosos en este área de la física (pero se olvida de físicos tan relevantes como Nima Arkani-Hamed).
La introducción justifica la escritura del libro y sus objetivos. Básicamente presentar las ideas de la teoría de cuerdas que hacen que la teoría sea atractiva para muchos físicos y que merece que los legos (dummies) conozcan.
Todas las partes se inician con una viñeta de Rich Tennant que contiene cierto toque de humor. El capítulo 1, «So What is String Theory Anyway?,» resume el libro y con ello toda la teoría de cuerdas en unas 12 páginas. El capítulo 2, «The Physics Road Dead Ends at Quantum Gravity,» trata de explicar por qué los físicos necesitamos una teoría cuántica de la gravedad. No me gusta que no se destaque que el problema es entender la naturaleza cuántica del espaciotiempo. Tampoco se destaca que la fuente de la gravedad en la teoría de Einstein es la energía, no la masa como en la teoría de Newton. Se menciona el problema de las singularidades (agujeros negros y big bang), la espuma cuántica de Wheeler en la escala de Planck y la unificación de las constantes de acoplo (que cambian con la energía) de las interacciones del modelo estándar. Se destaca el papel de la supersimetría en toda teoría cuántica de la gravedad y teoría de cuerdas en particular.
El capítulo 3, «Accomplishments and Failures of String Theory,» resume los logros teóricos pero destaca la ausencia de predicciones experimentales. Juan Maldacena y su correspondencia AdS/CFT se presentan como el mayor logro de los últimos años. No me gusta que el foco se ponga en que ciertos científicos creen que la teoría de cuerdas no ha cumplido sus objetivos originales. La teoría debería iluminar el problema de la energía oscura y se sugiere que quizás nunca lo logre. Más aún, acabar la primera parte con la sensación de que la teoría de cuerdas es un fracaso y que no tiene un futuro claro no me parece la mejor opción para un libro que se supone que explica dicha teoría. ¿Para qué explicarla si es un fracaso? Como lector no entiendo el énfasis en los fallos y la omisión de los logros.
La segunda parte se inicia recomendando, como no, otros libros de la serie de Wiley: Physics For Dummies, Einstein For Dummies, Quantum Physics For Dummies, y Astronomy For Dummies. El capítulo 4, «Putting String Theory in Context: Understanding the Method of Science,» trata de explicar qué es el método científico y la importancia de contrastar con experimentos las teorías (o hipótesis). Mencionar a Popper y Khun parece imprescindible, pero mencionar a Lee Smolin lleva a las guerras cuerdísticas. No me gusta este capítulo, cuya continuación «What You Must Know about Classical Physics,» cap. 5, discute las ondas estacionarias en una cuerda, la diferencia entre ondas transversales y longitudinales, y su conexión con la música. La naturaleza ondulatoria de la luz lleva al autor a mencionar el éter luminífero.
El capítulo 6, «Revolutionizing Space and Time: Einstein’s Relativity,» se inicia con el experimento de Michelson y Morley en busca del éter y nos lleva hasta las ideas básicas de Einstein. Se mencionan cuestiones al margen, como la acusación de plagio porque no dejó claro los hombros de gigantes sobre los que levantó sus ideas. La gravedad de Einstein permite mencionar las dimensiones extra del espaciotiempo de Nordström, Kaluza y Klein. El estilo de escritura permite una lectura rápida, pero el buen aficionado a la divulgación no puede esperar que el autor le cuente nada nuevo.
«Brushing Up on Quantum Theory Basics,» cap. 7, repasa la física cuántica, desde la termodinámica de Max Planck al experimento de doble rendija, pasando por la explicación del efecto fotoeléctrico de Einstein. ¿Conoce alguien el significado de la teoría cuántica? La interpretación de Copenhague y la de muchos mundos de Hugh Everett III nos llevan a las teorías de variables ocultas y a las unidades de Planck. ¿Son importantes estas cuestiones en teoría de cuerdas? En la opinión del autor hay una paradoja similar a la de Zenón en el germen de la teoría de cuerdas.

«The Standard Model of Particle Physics,» cap. 8, empieza con el electrón, su antipartícula el positrón, la electrodinámica cuántica y el concepto de diagrama de Feynman. Los nucleones llevan a los quarks y a la cromodinámica cuántica. Finalmente, los neutrinos permiten introducir la teoría electrodébil. Se menciona de pasada el problema de la jerarquía. «Physics in Space: Considering Cosmology and Astrophysics,» tras repasar la historia de los modelos cosmológicos, menciona la constante cosmológica y la expansión del espaciotiempo. La teoría del big bang de Gamow se compara con la teoría del estado estacionario de Hoyle. El mapa de las anisotropías del fondo cósmico de microondas obtenido por WMAP permite discutir la inflación cósmica, la materia oscura y la energía oscura. La radiación de Hawking de los agujeros negros da por finalizada la segunda parte del libro.
No me gustan estos capítulos introductorios, aunque quizás un lector completamente lego los necesite. Yo supongo que un lector de un libro de teoría de cuerdas no está interesado en leer unas 160 páginas de física bien conocida escritas por un buen divulgador. Se leen bien, pero creo que no aportan nada sustancial. La cuestión que me planteo es si un lector así realmente se atreverá a leer un libro de teoría de cuerdas. No tengo respuesta.
La teoría de cuerdas como tal aparece en la página 161, cap. 10, «Early Strings and Superstrings: Unearthing the Theory’s Beginnings,» al hilo de su historia. Tras una visión bastante particular de la situación de la física de los hadrones en los 1960, se menciona la fórmula de Veneziano y su interpretación en términos de cuerdas. La situación de la teoría en los 1970 se presenta como una historia whig, muy alejada de cómo nos gusta a los aficionados a la historia de la ciencia (la reseña del próximo martes será un buen libro sobre la historia de la teoría de cuerdas). No me gusta este capítulo histórico, pero quizás la razón sea que conozco fuentes más rigurosas. Quizás para un lector lego esté bien que un divulgador se reinvente la historia y la simplifique hasta el extremo. Quizás.
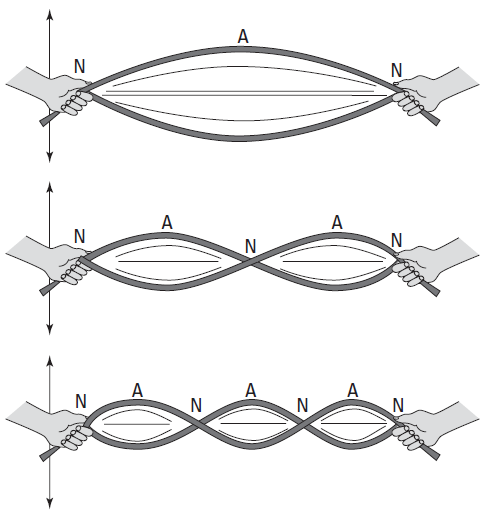
El capítulo 10 nos presenta la primera revolución de la teoría de cuerdas en 1984 y las cinco teorías de supercuerdas (tipo I, tipo IIA, tipo IIB, tipo HO y tipo HE). La descripción de cada teoría es muy parca. La tipo I tiene cuerdas abiertas y cerradas, presentando el grupo de simetría O(32). La tipo IIA contiene cuerdas cerradas «con patrones de vibración simétricos (no importa si vibran a la izquierda o a la derecha)» y cuerdas abiertas cuyos extremos están ligados a D-branas con un número impar de dimensiones. La tipo IIB contiene cuerdas cerradas «con patrones de vibración asimétricos (dependen de si vibran a la izquierda o a la derecha)» y cuerdas abiertas cuyos extremos están ligados a D-branas con un número par de dimensiones. Las supercuerdas heteróticas tipo HO y HE combinan cuerdas (bosónicas) que vibran hacia la izquierda y supercuerdas de tipo II que vibran hacia la derecha. La diferencia entre HO y HE es el grupo de simetría O(32) y E8 × E8, resp., siendo sus diferencias «importantes pero sutiles» (el autor no se atreve a detallarlas). ¿Cómo se compactifican las dimensiones extra del espaciotiempo? Usando variedades (complejas) de Calabi-Yau.
La segunda revolución de la teoría de cuerdas iniciada en 1995 se describe en el capítulo 11, «M-Theory and Beyond: Bringing
String Theory Together,» pág. 183. Se introduce la idea de la teoría M de Edward Witten como teoría que subyace a las cinco teorías de supercuerdas. Una teoría en 11 dimensiones (10 espaciales y 1 temporal), que describe branas de diferente dimensión y repleta de dualidades que muestran la teoría desde diferentes prismas, pero que describen la misma realidad. La clave son las dualidades T y S, que ya fueron introducidas en 1977 por Claus Montonen y David Olive, pero que llegaron a su esplendor a principios de los 1990 gracias a Ashoke Sen y Nathan Seiberg. Se mencionan como padres de la teoría M a Chris Hull, Paul Townsend y Witten.
Tras bautizar como dualidad topológica a la dualidad T (el origen usual es toroidal) se menciona que relaciona las teorías de supercuerdas tipo IIA y tipo IIB, y tipo HO y tipo HE (sin más detalles). La dualidad S (bautizada como fuerte-débil) permite relacionar las teorías tipo I y tipo HO, y la teoría IIB consigo misma (es S-autodual). Se menciona en varias ocasiones que las ecuaciones matemáticas de la teoría de cuerdas son extremadamente difíciles y que usan resultados matemáticos tan paradójicos como que 1+2+3+4+⋅⋅ =−1/12 (parece que el autor quiere asustar al lector lego). Se destaca, eso sí, que la supersimetría simplifica las ecuaciones y es clave para la red de dualidades, aunque sin más detalles.
La teoría M parte de la dualidad descubierta por Witten y Paul Townsend entre la teoría de supercuerdas en 10D y la supergravedad en 11D. Se menciona el gravitino y la aparición de branas (D-branas y p-branas). Se mencionan las D5-branas y las D3-branas, destacando que tienen tensión y cargas, las branas negras y su relación con los agujeros negros extremales, siempre sin detalles y recalcando que para el lego es imposible entender la diferencia entre los dos tipos de branas; el autor se atreve a afirmar que es tan imposible como que alguien que no haya estudiado religión conozca la diferencia entre las doctrinas teológicas episcopales y católica (por cierto, yo no tengo ni idea de la diferencia).
Se menciona la teoría matricial (M = Matriz) de Leonard Susskind, Tom Banks, Willy Fischler y Steve Shenker para la interacción entre 0-branas («partones» en la nomenclatura de Susskind). También la teoría holográfica de Gerard ’t Hooft (1993) y Susskind, la correspondencia AdS/CFT de Juan Maldacena y la conexión con la energía oscura. Finalmente se presentan los mundos brana de Savas Dimopoulos, Nima Arkani-Hamed y Gia Dvali (1998), y de Lisa Randall y Raman Sundrum (1999). Explicar la idea de que nuestro universo es una 3-brana en un espaciotiempo de mayor dimensión no parece difícil, lo que da pie a mencionar la teoría de gravedad localmente localizada de Lisa Randall y Andreas Karch (2000). También se menciona la teoría F de Cumrun Vafa (1996) que según el autor está de moda en la actualidad. Finalmente, se menciona el problema del paisaje y su relación con los principios antrópicos débil y fuerte de la mano de Leonard Susskind (2003).
En la página 209 da inicio el capítulo 12, «Putting String Theory to the Test,» que menciona la posibilidad de comprobar dos predicciones de la teoría (la supersimetría y la existencia de dimensiones extra) usando el LHC del CERN. Se comenta que estas pruebas no son una contrastación (demostración de la validez) de la teoría. Se menciona la posibilidad de observar la espuma cuántica preinflacionaria en el fondo cósmico de microondas, los defectos tipo cuerdas cósmicas y los efectos cuánticos en las ondas gravitacionales observadas con instrumentos como GEO600 (Alemania), no podía faltar Craig Hogan (2007). Se menciona que se pueden observar violaciones de la simetría Lorentz (usando rayos gamma ultraenergéticos) que mostrarían inconsistencias matemáticas (la teoría de cuerdas predice que la Naturaleza es invariante Lorentz y cualquier violación iría en contra de sus principios físicos).
La cuarta parte se inicia con el capítulo 13, «Making Space for Extra Dimensions,» que califica la idea de dimensiones extra del espaciotiempo como fascinante. La banda de Möbius, la botella de Klein, la geometría no euclídea y la teoría general de la relatividad de Einstein nos llevan a la pregunta: ¿por qué el espaciotiempo tiene cuatro dimensiones? Parece extraño, pero el hilo argumental llega hasta el libro de Jean-Pierre Luminet, «The Wraparound Universe» (2008) [si no lo conoces te lo recomiendo]. Se menciona la teoría cuántica de campos cuerdísticos de S. James Gates Jr. y Warren Siegel que interpreta la teoría de cuerdas en cuatro dimensiones (aunque se indica que la idea ha sido seguida por pocos expertos; por cierto, a mí me gusta mucho la idea). El autor no se moja (supongo que es normal, como no es físico sino divulgador…).
El capítulo 14, «Our Universe — String Theory, Cosmology, and Astrophysics,» presenta los modelos cosmológicos en teoría de cuerdas y teoría M. El universo eterno, la inflación eterna, el modelo ecpirótico, la colisión branas para explicar la inflación cósmica, el multiverso inflacionario, los universos burbuja de tipo Sidney Coleman y Frank De Luccia (1977), los universos paralelos, el futuro del cosmos en función de la dinámica de la energía oscura y el principio antrópico à la Weinberg para justificar todo. Como puedes suponer, muchos temas en pocas palabras requieren descripciones muy someras.
Un libro de teoría de cuerdos para un público lego, pero muy lego, debe discutir largo y tendido la idea de los universos paralelos y los viajes en el tiempo. No sé, yo no entiendo el porqué, pero parece que los grandes divulgadores lo tienen muy claro. «Parallel Universes: Maybe You Can Be Two Places at Once,» cap. 15, y «Have Time, Will Travel,» cap. 16, cumplen con este objetivo en el libro de Andrew Zimmerman Jones. Se recuerdan los tres niveles cosmológicos de universos paralelos de Max Tegmark (cosmólogo del MIT): nivel 1, si el universo es infinito debe contener una copia exacta de la Tierra en otro lugar, nivel 2, otras regiones lejanas del univeso pueden tener diferentes parámetros físicos, pero las mismas leyes físicas, y nivel 3, otros universos burbuja pueden tener incluso otras leyes físicas diferentes. Por supuesto, la historia de los universos paralelos empieza con Giordano Bruno y su ejecución como hereje.
El capítulo 16 sobre viajes en el tiempo discute los agujeros de gusano y la posibilidad de usar cuerdas cósmicas para su estabilización, idea de J. Richard Gott (1991). También se menciona la teoría M con dos tiempos de Itzhak Bars, un espaciotiempo de 13 dimensiones con 11 dimensiones espaciales y dos dimensiones temporales. Se menciona que ha propuesta una solución que evita los problemas asociados a probabilidades cuánticas negativas (y paradojas como la del abuelo), pero no se comenta en detalle. También se mencionan, ya que estamos, la paradoja de los gemelos y el modelo cosmológico que Gödel le regaló a Einstein.
La quinta parte discute las críticas y las alternativas a la teoría de cuerdas. El captíulo 17, «Taking a Closer Look at the String Theory Controversy,» empieza con las críticas de premios Nobel como Sheldon Glashow y Richard Feynman por su poco poder predictivo. Luego se mencionan los dos libros de 2006, Lee Smolin «The Trouble with Physics: The Rise of String Theory, the Fall of a Science,» y Peter Woit «Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law.» Se resumen todas las críticas en dos puntos básicos: la teoría de cuerdas no explica nada (es decir, no explica nuestro universo) y la teoría de cuerdas explica demasiado (es decir, explica todos los universos posibles). El argumento de autoridad de los gurú (se menciona a Witten) y la generación perdida de físicos brillantes nos recuerdan a los dos famosos libros.
«Loop Quantum Gravity: String Theory’s Biggest Competitor,» cap. 18, discute brevemente la gravedad cuántica de bucles (o lazos). Entre líneas leo cierto sesgo (comentarios como es que una teoría más específica a un problema concreto que la teoría de cuerdas). Los fundamentos son de Abhay Ashtekar (1986) e los interpretaron como «átomos» de espacio Lee Smolin, Ted Jacobson y Carlo Rovelli entre otros. Se afirma que la teoría contiene a los gravitones, es una teoría finita y describe el cosmos preinflacionario. Sesgos a favor que no le hacen ningún favor a un libro sobre teoría de cuerdas.
El capítulo 19, «Considering Other Ways to Explain the Universe,» menciona la teoría de triangulaciones dinámicas causales, la gravedad asintóticamente a salvo (asymptotic safety gravity), la grafidad cuántica (quantum graphity), la relatividad interna (internal relativity), la relatividad doblemente especial (doubly special relativity), la teoría MOND (Modified Newtonian Dynamics), e incluso la teoría de John Moffat sobre la velocidad de la luz variable. Un pastiche sin ton ni son que yo, personalmente, no veo que venga a cuento, salvo quizás para arremeter en contra de la teoría de cuerdas. La equidistancia que tanto gusta a los periodistas y comunicadores científicos cuando hablan de un tema del que no saben. Una pena.
Finalmente, el capítulo 20, «Ten Questions a Theory of Everything Should (Ideally) Answer,» presenta las diez cuestiones más obvias que toda teoría de todo, como la teoría de cuerdas, debe contestar: ¿qué es el bang del big bang? (preinflacionario), ¿qué es la energía oscura?, ¿por qué el tiempo corre hacia adelante?, y muchas otras que seguro que te puedes imaginar. El capítulo 21 presenta una breve biografía de diez teóricos de cuerdas: Edward Witten, John Henry Schwarz, Yoichiro Nambu, Leonard Susskind, David Gross, Joe Polchinski, Juan Maldacena, Lisa Randall, Michio Kaku y Brian Greene. Hecho en falta a mauchos y creo que Randall, Kaku y Greene están en la lista porque son personajes mediáticos muy famosos.
En resumen, un libro para legos, escrito por un lego. ¡Qué más se puede decir!









Hola Francisco,
Supongo que lees todos estos libros como parte de tu trabajo de documentación para escribir el tuyo. Muchas gracias por postear estas reseñas. Quizás podrías re-revisar (pues es muy probable que ya lo hayas leído) «El universo elegante», que es seguramente el texto de difusión más influyente y conocido en teoría de cuerdas. Ahora mismo estoy leyendo el «Little book of string theory», que presenta el tema de una manera algo distinta (variedades de Calabi-Yau por ejemplo ni siquiera se nombran); pero de la reseña que haces de «String theory for dummies» pareciera que éste último si sigue mucho más de cerca el libro de Greene.
Bueno, es una sugerencia. Posiblemente ahora eres el divulgador en español que conoce y tiene más frescos los temas esenciales de teoria de cuerdas, seria bueno saber si acaso el libro de Greene esta algo desactualizado, o sólo es muy conocido pero hay otros mucho mejores, etc. …
Saludos y gracias de nuevo por las reseñas.
Andrés, lo siento, pero el libro de Greene no estará entre las reseñas cuerdistas de los martes (ni el de Yau, ni el de Randall, ni tantos otros…). Aunque como «nunca puedo decir nunca jamás» quizás lo incluya después de las que están planificadas… (tengo muchos borradores ya escritos). Ya veremos si me apetece… pero no es mi objetivo reseñar lo que todo el mundo ya ha leído (¿para qué hacerlo si todo el mundo ya lo ha leído?).
Muchos autores de libros de divulgación sobre cuerdas inciden en la extrema complejidad de la teoría (la comparación del autor de este libro de esta complejidad con la teología es patética y es señal de que no entiende nada) lo que claramente echa para atrás a los potenciales lectores. Si bien es cierto que los detalles son muy complejos las ideas generales son bastante simples:
1º) En vez de considerar objetos puntuales de dimensión 0, sin extensión y sin diámetro lo cual conduce evidentemente a infinitos (y es claramente producto de una visión sesgada de nuestro punto de vista macroscópico) consideramos objetos de dimensión 1 (cuerdas).
2º) Estudiamos el lagrangiano, la acción y las ecuaciones de movimiento de una cuerda relativista.
3º) Cuantizamos la cuerda relativista de forma muy similar a como lo haríamos con un objeto puntual estableciendo condiciones de contorno en los extremos.
4º) Al cuantizar la cuerda relativista y al analizar sus vibraciones como si fuera un oscilador armónico encontramos ¡Una vibración que nos da el fotón ! y (bajo ciertas condiciones) ¡otra que nos da el gravitón! ¿CASUALIDAD? La única «pega» es que para que esto suceda el número de dimensiones del espacio-tiempo debe ser exactamente 26 (10 para las supercuerdas) ni una más ni una menos. ¿CASUALIDAD?
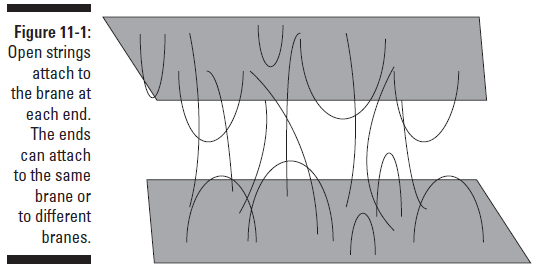
5º) Al estudiar las cuerdas abiertas nos encontramos que estas tienen que estar sujetas a unas nuevas entidades multidimensionales: las branas.
6º) De la dinámica entre cuerdas y branas pueden surgir la mayoría de propiedades del SM
Por supuesto los detalles son mucho más complejos y la variedad de modelos es enorme, pero para entender los fundamentos básicos solo hay que saber nociones básicas de relatividad, mecánica cuántica y teoría cuántica de campos.
Hola, unos comentarios estrictamente subjetivos. Primero que creo que hablar de las `String Wars´ es imprescindibles tanto desde el punto de vista histórico como desde el epistemológico, no hay que olvidar que las críticas a la Teoría de Cuerdas fueron (y son en parte) debidas a sus `taras´ metodológicas: su dificultad de testabilidad y refutabilidad empírica. Y luego está la cada vez más intrínseca relación Matemática Pura – Física Teórica, un asunto que está en el propio corazón de la Filosofía de la Física, y que en la Teoría de Cuerdas emerge de una manera que seguro que haría feliz al mismísimo Dirac 😉
Además, creo que Lisa Randall merece un puesto en cualquier libro de divulgación, aparte de por sus aportaciones teóricas (por sus papers, citaciones y actividades en conferencias, por ejemplo hace poco estuvo en Madrid junto con Tom Banks en el workshop «Fine-Tuning, Anthropics and the String Landscape«), porque ha sido una perfecta divulgadora en asuntos especialmente arcanos para el lego como son las dimensiones extra o el vínculo entre Física de Partículas y Cosmología .
Y por último, me parece que el sesgo anti-cuerdas que citas queda patente cuando se cita a Lee Smolin y a Peter Woit, y no se habla de la contraparte que le ha plantado cara incansablemente a base de argumentos sólidos: Lubos Motl. Para los que nos falta base matemática (o la tenemos oxidada), la comparación de argumentos y logros entre los protagonistas de uno y otro frente, son un elemento de juicio central para saber cómo esta el patio. Y ganan las Cuerdas por goleada.
Saludos.
Por cierto, en muchas partes de la matemática de la teoría de cuerdas se puede apreciar la intrincada relación entre matemáticas y física pero hay una en concreto, muy sencilla, que refleja esta relación de forma espléndida: cuando analizamos ciertos modos de vibración de las cuerdas (los modos transversales de Virasoro) nos encontramos con una expresión que contiene una constante a. Esta constante se puede expresar como a=1/2(D-2)(1+2+3+…). Donde D representa las dimensiones del espacio-tiempo. Aquí nos encontramos de nuevo con la suma de los infinitos números naturales. Además el valor de «a» aparece en el operador de la masa de la cuerda por lo que si a es infinito la masa de las cuerdas es infinita y la teoría de cuerdas se va a la papelera. Pero ahora la magia de las matemáticas emerge con toda su fuerza, aplicando el concepto de límite de sumas parciales o aplicando la función Z de Riemann (entre otros métodos) ¡encontramos un valor para esta suma infinita: -1/12 ! Si sustituimos este valor en nuestra expresión de a obtenemos: a=-1/24(D-2). Lo increíble es que este es el valor de «a» correcto para que la teoría sea consistente (en Física la suma de los infinitos números naturales tiene que valer -1/12). Además solo y exclusivamente si D=26 (a=-1) encontramos que las cuerdas abiertas tienen modos que incluyen al fotón (D=10 en supercuerdas). ¿Casualidad?
Planck:
1)Algo que yo no entiendo (y me gustaría mucho saber) es sobre las D0-branas, es decir he escuchado sobre los Matrix models (de la mano de Susskind) como un intento de formulación no perturbativa de la teoría de cuerdas, pero por ignorancia sigo pensando que son puntos… ¿Una teoría que contiene puntos puede ser finita? supuestamente eso es lo que se quería superar de la qft ordinaria y a pesar de los logros de SUGRA N=8 d=4 en su finitud hasta siete loops se dice que la teoría no puede ser definitiva pues es una teoría de puntos… si entonces cuerdas tiene por objetos fundamentales puntos… la verdad ya no entiendo
2) Muchos critican a la teoría por ser difícil de refutar. Francis dijo en un podcast que la teoría puede describir un mundo sin mecánica cuántica (no lo entiendo) y también un mundo sin relatividad general (tampoco lo entiendo), habló en un interesantísimo post que es posible describir un mundo sin susy. Concluimos, ya no que los modelos estándares de la cosmología y de la física de partículas sean predicciones genéricas ,si no que ni Qm ni GR ni SUSY lo son. ¿Entonces que predice genéricamente? a mi me parece que sólo que la naturaleza es lorentz invariante a toda escala.
¿Encontrar una violación a la simetría de Lorentz implica descartar cuerdas? ¿Alguien sabe?
planck:
Una disculpa mis comentarios anteriores eran generales quería decir algo sobre lo que comentas.
Esa cuenta es muy curiosa. Existen aritméticas (por ejemplo de tipo p-ádico) en donde estas cosas tienen sentido 🙂 ¿Será que hay algún tipo de estructura aritmética exótica subyacente en la teoría?. Habrá que ver, es un asunto delicado Molt es muy crítico con el prejuicio que tienen muchos sobre preferir lo discreto a lo continuo y la formulación de la teoría sin un fondo fijo.
Ojalá Francis hable de este asunto de la emergencia del espaciotiempo en su libro me muero de ganas por leer esto.
P.D. se me acaba de ocurrir que tal vez la teoría M tenga a susy como predicción genérica pues aquí supongo no se puede formular una versión «susy-free» pues el límite a baja energía de dicha teoría tiene que ser SUGRA maximal. (Conjeturo)
Saludos planck
Cierto Ramiro, con los números p-ádicos ciertas sumas infinitas parece que tienen sentido. Además estos números son fundamentales en teoría de números y se utilizan para intentar cuantificar escalas sub-plankianas. Lo más curioso es que parece haber una sub o una super-estructura dentro de los números que usamos habitualmente (números reales) y la naturaleza la utiliza en su nivel más fundamental de forma que nuestras reglas aritméticas cotidianas no sirven para explicar la física fundamental. Los mismos números complejos, en los que se basa toda la MC, parecen surgir de «añadir» una nueva «dimensión» a los números reales, de hecho, C es isomorfa a R^2. Quizás (esto ya es especulación mía) estas estructuras dentro de los propios números sean un reflejo de una estructura multidimensional del espacio-tiempo.
En mi opinión la Física del siglo XXI será (ya es) Física-Matemática. A falta de claras evidencias experimentales de las teorías más punteras características como la consistencia matemática, la coherencia interna, la generalización a espacios similares al nuestro y la eliminación de todas las alternativas posibles tendrán cada vez más importancia. Por esto, conocer los intrincados detalles de la relación entre Física y Matemáticas será fundamental en un futuro para evaluar en que grado una teoría Matemática tiene conexiones con nuestro mundo real.
Un saludo.
El asunto de los números reales no está libre de polémica, por ejemplo: ¿Todos los resultados de los experimentos son números racionales?. Todo esto es extraordinariamente sutil, cito algunos ejemplos:
1) Si fuese verídica la posibilidad de construir un ordenador que computara números reales entonces sería posible resolver problemas Np en tiempo polinomial. Pero justamente el límite de Bekeinstein y el principio holográfico prohiben tal grado de exactitud (en principio infinita).
Un enlace interesante al tema de la hipercomputación: https://en.wikipedia.org/wiki/Hypercomputation
2) Que alguien me corrija si me equivoco. Aceptando lo anterior, si los números reales no tienen un papel fundamental ¿Entonces qué clase de aritmética es la «adecuada»?, Sea cual sea la respuesta es dramática, que yo sepa no hay muchas posibilidades salvo los números p-ádicos (en el sentido de buscar un campo que extienda a los racionales y no sea trivial: es decir adjuntar un número finito de elementos transcendentes sobre Q).
¿Geometría tropical podría ser otra posibilidad?
Por cierto yo soy fan de un canal de YouTube en donde se imparten cursos de matemáticas por ejemplo este de topología algebraica: https://www.youtube.com/watch?v=kdpbfOzkJzI ¿Qué tienen de especiales? me encantan porque el autor tiene problemas con los números reales y define algo llamado «rational trigonometry» en donde rechaza a los reales y construye todo lo relevante para sus cursos usando racionales ¡Es fantástico!. si es una complicación… no lo sé, pero es algo atípico y a mi me parece que muchas cosas se vuelven mas intuitivas. Vale la pena.
3) La razón de esto es que yo al menos estoy muy emocionado pues vivimos en una época en la que se habla del espaciotiempo como un fenómeno emergente y ya no se hace en plan filosófico si no como una guía para continuar ej. ER=EPR, la paradoja AMPS, códigos holográficos, tensor networks, ads/cft, corrección de errores cuánticos etc.
Por cierto aquí están los comentarios de Molt sobre la independencia de fondo en teoría de cuerdas http://motls.blogspot.mx/2012/12/what-is-background-independence-and-how.html
Un placer planck.
Saludos.
Interesante lo que comentas Ramiro e interesantes también los enlaces. Parece que los números esconden grandes secretos, por ejemplo, algunos piensan que la función zeta de Riemann esconde una estructura Física fundamental en su interior. Es muy posible que nuevas herramientas matemáticas consigan importantes avances en Física en un futuro próximo. Yo sigo pensando que es casi imposible que las teorías de cuerdas sean solo un artificio matemático sin conexión con la realidad, hay demasiados indicios tanto físicos como matemáticos que indican lo contrario. Necesitamos nuevas herramientas matemáticas que nos permitan un análisis no perturbativo de la teoría, quizás entonces, los secretos más profundos de la gravedad y del espacio-tiempo nos sean por fin revelados. Un saludo.
Un comentario sobre las clases de N J Wildberger y olvidándonos de la física un momento (no me gustaría que quedase la impresión de que es un crackpot por no gustarle los números reales).
Es interesante lo que hace al «racionalizar» curvas y variedades. Y tiene sentido por que lo que hace es casi equivalente a tropicalizar una variedad, esto en el sentido de que se puede definir suavidad a trozos y estudia propiedades maravillosas que surgen de esto como esta:
Sea X curva plana, sea g su gérnero y b su primer número de betti, entnces g(x)>b(R(X)) donde R(X) es la racionalización de la variedad que en este caso se puede ver como la tropicalización de X
Es muy bonito lo que se hace en sus cursos. Dar las parametrizaciones racionales de muchos objetos famosos en geometría es encantador, de verdad recomiendo sus cursos.
Otro ejemplo sencillo de que no es tan malo alejarse de los reales es simplemente considerar dos curvas (suaves a trozos) que se saben difeomorfas e ismométricas y preguntar si usando solo puntos racionales sobre ellas puedes deducir que son equivalentes (en el sentido anterior) y la respuesta es que si , más aún estudiando al anillo de funciones racionales sobre las curvas puedes establecer su clase de equivalencia exactamente como se haría considerando los grupos de difeomorfismos isométricos sobre ellas.