El 25 de agosto de 2015, Stephen Hawking anunció que había resuelto el problema de la información en agujeros negros usando supertraslaciones BMS. Su breve charla dejó muchas dudas entre los expertos. Prometió un artículo que hoy se publica como regalo de reyes para todos los amantes de la física. Bueno, en realidad, este artículo nos muestra la idea pero Hawking nos regala la primera parte del artículo. Afirma que habrá un segundo artículo con los detalles.
El artículo HPS es Stephen W. Hawking, Malcolm J. Perry, Andrew Strominger, «Soft Hair on Black Holes,» arXiv:1601.00921 [hep-th]. Si te apetece leer otra crítica temprana te recomiendo Lubos Motl, «Hawking, Perry, Strominger on soft hair,» The Reference Frame, 06 Jan 2015. [PS 07 Jan 2016] También puedes leer una buena revisión del artículo en Sabine Hossenfelder, «More information emerges about new proposal to solve black hole information loss problem,» BackReaction, 07 Jan 2016.
Te recuerdo el problema. La mecánica cuántica prohíbe que la información se destruya (la evolución unitaria es siempre reversible), aunque puede codificarse de forma intrincada de tal forma que en la práctica sea imposible recuperarla (cuando quemas carbón de los reyes obtienes cenizas a partir de las cuales no puedes reconstruir la forma original del carbón). Cuando una estrella colapsa para dar lugar a un agujero negro toda su información cuántica queda atrapada dentro de su horizonte de sucesos. Como un agujero negro tiene temperatura emite radiación de Hawking, que es térmica. ¿Contiene dicha radiación información sobre la estrella original? Según la mecánica cuántica debería contenerla (igual que en el caso del carbón de reyes). Pero los agujeros negros «no tienen pelo» (solo tienen masa, carga eléctrica y momento angular). ¿Dónde se almacena dicha información cuántica? ¿Viola la física de los agujeros negros la física cuántica?
La solución más lógica para la paradoja de la información cuántica en los agujeros negros es que alguna de las hipótesis del teorema clásico que afirma que los agujeros negros no tienen pelo no se cumple debido a fenómenos cuánticos. La propuesta de Hawking está en la línea de su famosa afirmación de marzo de 2014: «los agujeros negros no existen». Recuerda que Hawking afirmó que no existen agujeros negros con «horizonte verdadero» sino que sólo existen «agujeros negros» con horizonte aparente. Estos «agujeros negros» son tan parecidos a los agujeros negros como se necesite, pero su horizonte aparente permite violar una de las hipótesis del teorema que afirma que los agujeros no tienen pelo.
La propuesta de Hawking de agosto de 2015 es que los «agujeros negros» son soluciones de las ecuaciones de Einstein tipo espaciotiempo asintóticamente plano con cargas BMS (que son versiones generalizadas del momento angular). Un «agujero negro» puede tener infinitas cargas BMS en su horizonte aparente según la física clásica, luego puede almacenar una cantidad infinita de información en ellas. Pero esto no basta para resolver la paradoja de la información. La idea de Hawking es que la física cuántica de alguna forma impone un corte en el número de cargas BMS del «agujero negro» reduciendo su número exactamente al necesario para explicar la entropía de Bekenstein–Hawking de los agujeros negros.
Por desgracia, el nuevo artículo de Hawking, Perry y Strominger no ha logrado cumplir los deseos navideños de Hawking para todos los amantes de la física. Este regalo de reyes nos deja con la miel en los labios. Todavía no se ha logrado construir una solución clásica tipo «agujero negro» con cargas BMS (con «pelo» en supertraslaciones) que presente un «horizonte aparente» y que se asemeje a un agujero negro sin «pelo» (solución de Kerr–Newman). Sin un modelo explícito de las supertraslaciones no sabemos estudiar sus propiesdades cuánticas. El nuevo artículo sugiere que las supertraslaciones podrían estar codificadas de forma cuántica en gravitones con energía cero (soft gravitons). Sin embargo, no ofrece detalles firmes (se ha avanzado muy poco en esta idea desde el trabajo de Weinberg en 1965).
El nuevo artículo HPS promete más de lo que ofrece. Como resulta más fácil trabajar con agujeros negros cargados se estudia el análogo electromagnético a los gravitones con energía cero, los fotones con energía cero (soft photons). Se argumenta que la longitud de onda de estos «fotones» (soft photons) está limitada por la escala de Planck, que actúa como corte para su número. Más aún, se argumenta que el número finito de estos «fotones» es proporcional al área del horizonte del agujero negro. Se concluye en la sección final del artículo que con los «gravitones» (soft gravitons) debería ocurrir lo mismo. Su número debería ser finito y proporcional al área del horizonte de sucesos. Pero en este artículo no se prueban estos hechos. Los autores proponen que un futuro artículo podría atacar este problema.
No he querido entrar en detalles técnicos. Quienes hayan estudiado algo sobre las cargas BMS de Bondi, van der Burg, Metzner y Sachs (1962) pueden recurrir al artículo para disfrutar de los detalles. Las supertranslaciones son transformaciones matemáticas de un espaciotiempo vacío asintóticamente plano en otro espaciotiempo vacío que no es equivalente al original. Por supuesto, la simetría de las supertraslaciones debe estar rota y esta rotura de simetría debe estar acompañada de bosones de Goldstone sin masa; estos bosones son los «gravitones» de energía cero (soft gravitons) que formarán el «pelo» de energía cero (soft hair) de las soluciones tipo «agujero negro». En 1965, Weinberg demostró que hay un análogo a las supertraslaciones en un campo electromagnético y que la rotura de su simetría produce «fotones» de energía cero (soft photons).
El teorema de Weinberg ha sido la inspiración del trabajo Strominger durante el último lustro y éste la de Hawking durante el último año. Sin embargo, trabajar con «gravitones» en lugar de con «fotones» es muchísimo más complicado y, como nos muestra el nuevo artículo HPS, todavía está más allá de lo que físicos de cierta edad (como Hawking, Strominger y Perry) pueden lograr. Quizás físicos teóricos jóvenes tengan la sagacidad suficiente para completar los detalles de la propuesta HPS y lograr lo que soñó Weinberg en 1965. Dicho logro será la base para resolver la paradoja de la información en los agujeros negros. Pero todavía queda mucho trabajo por realizar.


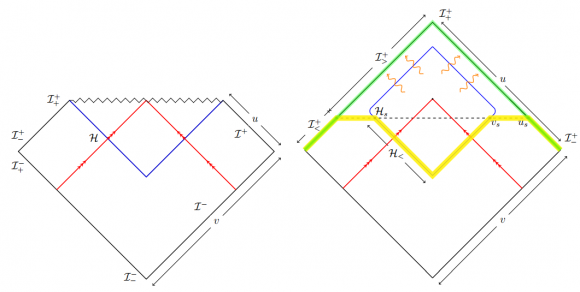


Es increíble siquiera que seamos capaces de hacer conjeturas plausibles sobre lo que sucede dentro de un AN, el poder de la Física y de las Matemáticas parece «sobrenatural». Si alguien no lo cree que analice esta frase del paper: «Indeed in this paper we show that soft hair has a natural description as quantum pixels in a holographic plate. The plate lives on the two sphere at the future boundary of the horizon. Exciting a pixel corresponds to creating a spatially localized soft graviton or photon on the horizon…» Increíble el poder de la dualidad ADS/CFT.
Con mis limitados conocimientos creo que aunque el paper es interesante, como se esperaba, está muy lejos de solucionar nada sustancial en torno a la paradoja de la información en AN. Creo que es otro «paper» anómalo de Hawking y SP: es un trabajo incompleto que deja muchas cosas sin resolver con la promesa de hacerlo en un futuro, el concepto de graviton de energía cero no está nada claro y como dice Lubos parecen obviar muchos de los avances entorno a la dualidad ADS/CFT. Sin embargo, la idea de la simetría BMS como origen de nuevas cargas conservadas donde pueden residir la enorme cantidad de grados de libertad de un AN parece muy interesante aunque por otro lado, como ellos mismos reconocen, conseguir calcular la entropia de BH a partir de estos infinitos estados es, de momento, imposible.
De todas formas es otro pequeño paso hacia adelante, los próximos trabajos prometen ser apasionantes. Por cierto, ¿que pensarán los filosofetes de estas cosas? A ver si acierto: «Si Popper levantara la cabeza…» 🙂
Ich habe bis dato noch nirgends eine richtige Zeichnung von einem kūnstlichen schwarzen Loch fūr Raumschiffe gesehen!
Many years ago and I cannot see a right picture from a spacecraft black hole. A black hole for spacecraft working very different to the thinking from Stephen Hawking!
Por cierto, sobre este tema Lubos dice unas cuantas cosas interesantes que me gustaría poner aquí:
– La mayoría de expertos en gravedad cuántica creen (según el) que la RG es solo una teoría aproximada a cortas distancias y que a pequeñas escalas la MC prevalecerá y la RG solo se cumplirá de forma aproximada. Personalmente encuentro esto más plausible que lo contrario puesto que ya hay trabajos que indican que las ecuaciones de la RG se pueden obtener a través de fenómenos cuánticos como la entropía de entrelazamiento. Esto significa que la unitariedad que predicen M-theory y ADS/CFT prevalecen sobre la RG y la información es probablemente conservada en un AN.
– El horizonte de sucesos no es algo estático a nivel cuántico, su posición y la geometría del AN depende de toda la historia pasada y futura del AN por lo que suponer que todos los grados de libertad viven justo ahí tiene muchos problemas. Esto nos lleva a la gran pregunta sin resolver: ¿Donde se localiza FÍSICAMENTE el borde conforme donde viven los grados de libertad de un AN? En mi opinión esta es la gran pregunta a resolver y muestra de nuevo la intricada relación entre Física y Matemáticas. La solución probablemente nos diría la respuesta a la mítica pregunta ¿Donde va la materia que cae en un AN?
Los AN esconden la respuesta a los misterios más grandes y más profundos de la Física, que podamos estudiar estos objetos a través de la Física y las Matemáticas es una de las cosas más sorprendentes y fascinantes que existen.
Francis, cuando decimos que no podemos obtener de nuevo el carbón de las cenizas ¿es un problema de tecnología o una imposibilidad intrínseca de la naturaleza?
Francis, sólo soy un estudiante de Física y mis conocimientos son limitados, pero ¿puedes explicarme por qué la gente sigue tomando en serio a S Hawking? Hasta donde llego, sus únicos m’eritos son éstos, y no son suyos:
– los agujeros negros hacen desaparecer entropía (planteado y resuelto por Bekenstein)
– los AN se evaporan con radiación de Hawking (planteado y resuelto por Zel’dovich)
– los agujeros negros sí tienen pelo (pero no explica por qué; todos suponemos q tienen pelo, pero el caso es cómo funciona)
– y los teoremas de singularidad (junto con Penrose, y aquí sí que no alcanzan mis conocimientos para medir su importancia)
Y no me parece serio, ni sus títulos de artículos ( Blackhole explosions?; The wave function of the Universe, Black holes do not exist, The end of theoretical physics…), ni estas tomaduras de pelo de avanzar un gran notición que queda en gran bluff.
De verdad que no lo comprendo. Espero de verdad que a medida que aprenda más física esto tenga explicación.
Un saludo.
Carlos F, cuando estudies los artículos de Hawking, si lo haces algún día, y los compares con artículos de otros físicos comprenderás que sus ideas son brillantes y profundas. Por supuesto, sus artículos de los últimos 10 años son peores que sus artículos de hace 50 años (la edad afecta a todo el mundo).
Siendo así, le matendré el beneficio de la duda. Pero es que la altanería y el poco respeto que muestra por el trabajo de los demás en «Historia del tiempo» me daba rechazo. Gracias por la respuesta.