La frase «se observa un buen acuerdo con las predicciones del modelo estándar» parece decorar todos los artículos sobre física de partículas basados en colisiones del LHC. Sin embargo, no se debe olvidar que en las primeras observaciones de un fenómeno conocido conforme crece la energía de las colisiones suelen aparecer desacuerdos con las predicciones teóricas (aunque a menos de una sigma). Por ello, los métodos de Montecarlo que usan para calcular estas predicciones deben ser calibrados de forma periódica. Así, de vez en cuando, se publican artículos en cuyo resumen se afirma que «se observan desacuerdos entre los valores de ciertos observables y las prediciones del modelo estándar». No hay que asustarse, pues tras la calibración adecuada de los códigos (a veces dando lugar a una nueva versión de los mismos), dicho desacuerdo suele desaparecer.
Un buen ejemplo es el último artículo de CMS sobre la sección eficaz asociada a la desintegración de quarks top en parejas de leptones con 35.9 /fb de luminosidad integrada en 2016; la colisión protón contra protón produce un pareja top-antitop que se desintegra en dos leptones cargados, dos neutrinos y dos chorros hadrónicos asociados a una pareja bottom-antibottom. Las predicciones de los diferentes códigos de Montecarlo usados por CMS (MG5 aMC@NLO, MG5 aMC@NLO, PYTHIA8, MADSPIN, etc.) difieren entre sí y, más aún, discrepan de las observaciones experimentales. Por supuesto, esto no significa que el modelo estándar sea incapaz de predecir estas desintegraciones; solo indica que hay que recalibrar los códigos.
El artículo (que aún no está en arXiv) es CMS Collaboration, «Title Measurements of differential cross sections for ttbar production in proton-proton collisions at 13 TeV using events containing two leptons,» CMS-PAS-TOP-17-014, CDS 06 Jun 2018 [PDF]. Me he enterado gracias a Luboš Motl, «Monte Carlo fails at leptonic top pair production,» TRF, 06 Jun 2018.
[PS] Perdón a todos los lectores porque he cometido un error imperdonable en la primera versión de esta entrada. Un bosón W tiene carga eléctrica positiva (o negativa), luego solo se puede desintegrar o bien en un antileptón cargado con carga positiva (o un leptón cargado con carga negativa) y un neutrino (o un antineutrino), o bien en un quark (antiquark) de tipo arriba de carga +2/3 (−2/3) y un antiquark (quark) de tipo abajo de carga −1/3 (+1/3). La ley de conservación de la carga eléctrica prohíbe que se desintegre una pareja leptón-antileptón. Siento mucho haberlo sugerido en la primera versión de esta entrada. He cometido un despiste imperdonable, similar a demostrar que 1=0 y creerse que la demostración es correcta. Perdón a todos. Muchas gracias @VM_Lozano, por haberme hecho sonrojar. [/PS]
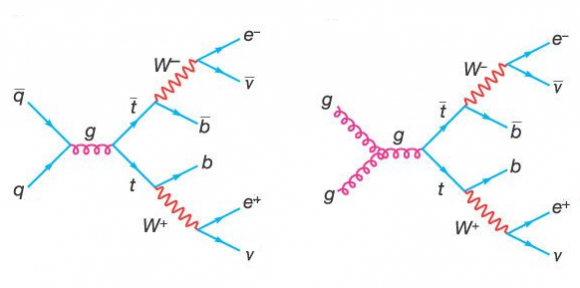
Como muestra este diagrama de Feynman, la colisión protón contra protón produce la aniquilación quak-antiquark o la fusión de dos gluones que dan lugar a un gluón de alta energía que se desintegra en un par quark-antiquark top (o un par top-antitop), pp → tt. El top (antitop) se desintegra en un quark bottom (antibottom) y un bosón W, desintegrándose este último en un leptón cargado y otro neutro (por cierto, el leptón neutro puede tener el mismo sabor o un sabor diferente al leptón cargado). El canal pp → tt → 2b2ℓ2ν, donde ℓ = e o µ, se observa como dos chorros hadrónicos y dos leptones cargados (dos electrones, dos muones, o un electrón y un muón), pues los neutrinos no se detectan (se observan de forma indirecta como una pérdida de energía tras calcular la cinemática de la desintegración). Por cierto, la interacción débil permite cambios de sabor, con lo que el neutrino (antineutrino) puede ser de sabor igual o diferente al antileptón (leptón) cargado; desde el punto de vista de la pérdida de energía el sabor de este leptón neutro es irrelevante.
Los métodos de Montecarlo para el cálculo de los observables asociados a este canal de desintegración alcanzan una precisión NLO (next-to-leading-order, en inglés el orden siguiente al dominante, es decir, a segundo orden). La gran fuente de incertidumbre son las distribuciones de partones (PDF) que describen el factor de forma de los partones (gluones) que colisionan. Casi con toda seguridad la discrepancia entre los datos y la predicción teórica es debida a errores sistemáticos, con lo que se resolverán cuando se calibren los métodos de Montecarlo; o en todo caso cuando se introduzcan correcciones de mayor orden (N²LO).
Podemos soñar un poco y recordar que la esperanza de muchos físicos es que esta calibración no sea suficiente y se oculte nueva física en esta pequeña discrepancia. Lo siento, pero en mi opinión es una esperanza vana.



Super interesante. En ingeniería civil usamos bastante los métodos de Montecarlo y resulta fascinante la exquisitez necesaria en dicho método para la física. Gracias, Francis por divulgar estos temas.
hola Francis,
Esta interpretación del papel de CMS es una caricatura. No hace justicia al trabajo inmenso de los autores de generadores Monte Carlo, que han producido herramientas muy sofisticadas. Es cierto que los generadores requieren una calibración para ajustar los parámetros en el modelado de fenómenos donde no tenemos cálculos de precisión, como por ejemplo la hadronización. Es un proceso que no se presta a cálculos con el método de calculo de perturbación. Por lo tanto los autores de MC han creado un modelo fenomenologico, cuyos parámetros fijamos en el proceso tuning del MC.
La distribución de pT de los quarks top, que es la distribución que más problemas da, no debería depender mucho de estos parámetros. El hecho que encontramos varios generadores que predicen distribuciones muy diferentes ya indica que hay un problema, probablemente en el interfaz entre elemento de matriz y el modelo de «parton shower». Que ninguno de los generadores sea capaz de reproducir todas las distribuciones es un problema gordo. Desde luego no es una cuestión de un poco de calibración y arreglado.
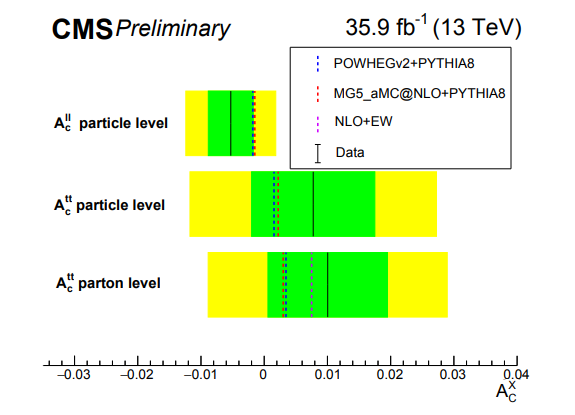
Y no acaba aquí. En el mismo papel se comparan las medidas con las predicciones más sofisticadas y encuentran un desacuerdo como una casa. Estos son cálculos de «first principle», que no se pueden «calibrar» cuando están en desacuerdo con los datos. En la figura 46 cuantifican este desacuerdo. La probabilidad de que la predicción sea la teoría correcta para los datos es menos de un por mil, un desacuerdo mucho más grande que los muchos «hints» de física nueva que circulan en los blogs.
Puede que CMS se equivocara, pero el resultado ha pasado el escrutinio de una colaboración de casi 3000 personas. Además, los resultados a 7 y 8 TeV de CMS y ATLAS ya apuntaban a este problema, aunque con menos claridad.
Puede que falle algo en el calculo o la estimación de la incertidumbre. Pero repito que es uno de los cálculos más solidos que tenemos en el LHC (técnicamente es NNLO + NNLL, donde cada N representa años de trabajo de varias personas).
Puede que sea una señal de física más allá del Modelo Estándar. Desde luego no estabamos pensando en esto cuando rezábamos para que hubiera algún desacuerdo con el Modelo Estándar, pero quién sabe como serán esas señales.
La verdad es que no tenemos ni idea. Solo sabemos que unos de los cálculos más solidos que tenemos falla cuando se enfrenta a los resultados de unos de los análisis más esenciales que hacemos. Te puedo asegurar que ninguno de los asistentes de la conferencia LHCP en Bologna la semana pasada dijera «pues, vaya, habrá que modificar la predicción, a calibrar el Monte Carlo», cuando se presentó este resultado. Encontraras más información en la presentación de Javier Fernandez de la Universidad de Oviedo (http://lhcp2018.bo.infn.it/programme.html#fh5co-agenda -> plenaria del viernes).
Siento el sermón, pero todo esto representa un trabajo muy concienzudo de muchas personas. Sería una pena que en el último paso (el de divulgación) se creara una impresión equivocada.
Gracias, Marcel.
Hola,
gracias Marcel por el comentario tan acertado aclarando la situación y gracias Francis por divulgar algo que no es tan sencillo o llamativo de divulgar como una búsqueda directa o física del bosón de Higgs.
Yo también creo que la visión de Motl en esto no es acertada y además es errónea cuando dice que los MCs fallan al predecir cualquier observable cinemático. Lo único que se puede sentenciar es que no hay ningún MC que prediga con buen acuerdo todas las distribuciones. Y la discrepancia no es pequeña en absoluto desde luego, y es de las que más lleva en el «mercado» (desde el Run1).
Además hay que claramente distinguir entre observables a nivel de partícula (particle level) en el espacio fiducial del detector, donde la predicción de algunos observables se puede más o menos «sintonizar», y a nivel de parton (parton level) en el espacio total de fases, donde el cálculo es más complicado y las incertidumbres de Parton Shower son mayores.
Añadir también que ATLAS también tiene resultados a 13TeV apuntando este problema, e.g.:
https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PAPERS/TOPQ-2017-01
https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PAPERS/TOPQ-2016-01
https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PAPERS/TOPQ-2016-04
y que la solución no parece fácil pues subir una «N» más en el cálculo de los elementos de matriz ya no es trivial y hacerlo en el parton shower menos aún, y la clave como dice Marcel puede estar en cómo se está haciendo la combinación de ambos (ME+PS)…
Gracias
Javi
Gracias, Javier.