La mecánica cuántica es sutil, sobre todo cuando se aplica a seres humanos o sistemas macroscópicos en un experimento mental (Gedankenexperiment). Al aplicar la evolución unitaria a dichos sistemas se tiende a introducir colapsos de la función de onda que no están justificados, lo que lleva a contradicciones e incoherencias. Así ocurre con supuesta incoherencia de la mecánica cuántica publicada por Frauchiger y Renner en Nature Communications usando una variante del experimento mental del amigo de Wigner. Su razonamiento contiene el mismo error que ellos destacan en el experimento de Wigner, pero que esconden bajo la alfombra al usar cuatro observadores y un orden temporal en las medidas. Por ello sus conclusiones son incorrectas.
No tenía pensado hablar de este experimento mental, que ya recibió bastante eco mediático en 2016 y fue refutado en varios blogs. Ni siquiera tras su renovado eco mediático (con cambio de título) tras su publicación en una revista prestigiosa. Sin embargo, tras ser tratado en el Ep. 186 del podcast de Coffee Break: Señal y Ruido [a partir del min. 105], en el que no pude participar, creo que debo realizar una oportuna aclaración. Mis amigos contertulios olvidaron aclarar que el análisis cuántico del artículo es incorrecto. Y por tanto sus conclusiones son falsas. La mecánica cuántica se puede aplicar tanto a los sistemas macroscópicos como a los microscópicos. Solo aparece una incoherencia en el primer caso si se aplica mal y se cometen errores sutiles, como en este caso.
El artículo es Daniela Frauchiger, Renato Renner, «Quantum theory cannot consistently describe the use of itself,» Nature Communications 9: 3711 (18 Sep 2018), doi: 10.1038/s41467-018-05739-8, arXiv:1604.07422 [quant-ph]; nótese que la primera versión del artículo tenía un título muy diferente, «Single-world interpretations of quantum theory cannot be self-consistent,» arXiv:1604.07422v1 [quant-ph]. En esta entrada discuto estos artículos siguiendo a Mateus Araújo, «If your interpretation of quantum mechanics has a single world but no collapse, you have a problem,» More Quantum, 20 Jun 2016, y en especial su resumen del problema en «The flaw in Frauchiger and Renner’s argument,» More Quantum, 24 Oct 2018.
[PS 30 Oct 2018] Recomiendo la lectura de Guang Ping He, «Quantum theory has no problem consistently describing the use of itself,» arXiv:1810.06858 [quant-ph], y Liang Chen, Ye-Qi Zhang, «Comments on «Quantum theory cannot consistently describe the use of itself»,» arXiv:1810.01080 [quant-ph]. [/PS]
[PS 17 jun 2021] Antonio Bernal, «On the paper «Quantum theory cannot consistently describe the use of itself»,» arXiv:2106.07312 [quant-ph] (14 Jun 2021), comenta otro error en la demostración (que él llama «un pequeño detalle» que hace que la demostración sea incompleta). Muchos otros artículos han encontrado errores argumentales. [/PS]

Hay que empezar por el principio, el experimento mental del amigo de Wigner [PDF], que fue refutado por David Deutsch, «Quantum theory as a universal physical theory,» International Journal of Theoretical Physics 24: 1–41 (1985), doi: 10.1007/BF00670071. La idea de este experimento mental es razonar sobre si la evolución unitaria de la mecánica cuántica se puede aplicar a un observador que observa; en la versión original de Wigner se trata de una persona (sistema macroscópico consciente), pero que en la formulación actual se aplica a cualquier sistema macroscópico que pueda realizar una medida cuántica.
Supongamos que Wigner () está fuera de un laboratorio perfectamente aislado en cuyo interior se encuentra su amigo (
) que realiza una medida cuántica de un cúbit (bit cuántico) cuyo estado inicial es
. El amigo realiza un medida del cúbit (sin que Wigner lo sepa), resultando el estado
. Para dejar constancia de la medida, el amigo escribe el resultado (
) en una nota (o prepara un cúbit con dicho estado) que saca fuera del laboratorio. El estado ahora es
.
Ahora es el turno de Wigner, que realiza una medida sobre el sistema completo, formado por el laboratorio, su amigo y el cúbit medido. Asumiendo que la evolución de dicho sistema completo ha sido unitaria hasta ese momento, puede deshacer la medida de su amigo mediante la aplicación de una transformación unitaria (una puerta de Hadamard, que transforma un cúbit en un estado de Bell y viceversa). Por supuesto, el proceso afecta a la memoria (consciente) del amigo, que es borrada (con lo que el amigo olvida qué resultado obtuvo en su medida). El estado resultante es . ¿Has notado ya dónde se encuentra el error?
Wigner y su amigo discuten sobre el resultado obtenido. Wigner afirma con certeza que la medida del cúbit ha dado (cero). El amigo no recuerda el resultado que obtuvo, pero encuentra fuera del laboratorio la nota (
), donde aparecerá o bien un
(cero), o bien un
(uno) con igual probabilidad (si el experimento se repite muchas veces); dicha información le indica que el estado del sistema es o bien
, o bien
, luego la medida del cúbit ha dado
, o
con igual probabilidad (50%). En apariencia se ha llegado a una contradicción. La medida del mismo sistema físico realizada por dos observadores diferentes conduce a valores que pueden ser diferentes.
Por supuesto, en apariencia y solo en apariencia. ¿Has notada ya dónde se encuentra el quid de la cuestión? La razón es que hemos supuesto que Wigner realiza una operación cuántica sobre un sistema que ha evolucionado de forma unitaria, es decir, en un sistema en el que el amigo ha realizado una medida usando una transformación unitaria (sin colapso). Pero según la mecánica cuántica, toda medida requiere un colapso. Según las leyes de la mecánica cuántica, el estado sobre el que Wigner aplica la transformada de Hadamard no está en superposición, siendo o bien , o bien
. Por tanto, tanto Wigner como su amigo acabarán estando de acuerdo sobre el resultado de la medida del cúbit dentro del laboratorio. Un 50% de las veces ambos coincidirán en que era
(cero), y el otro 50% de las veces en que era un
(uno).
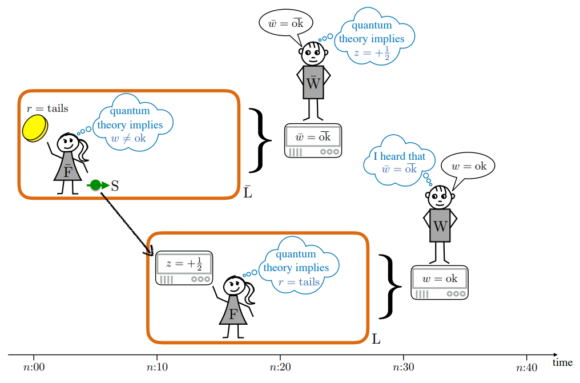
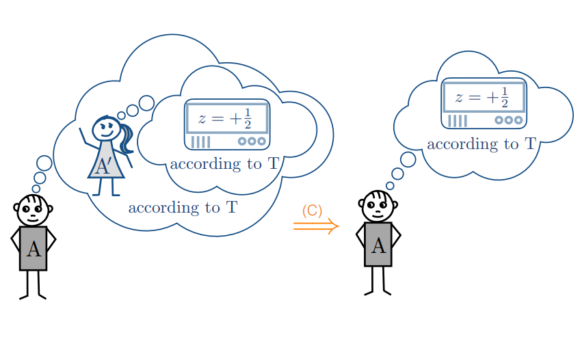
El problema, repito, es asumir que un observador que ignora que se ha realizado una medida cuántica, puede obtener un resultado correcto tras realizar una medida cuántica posterior, asumiendo que nunca antes realizó dicha medida. El gato de Schrödinger en la caja está vivo o muerto, no pudiendo estar en una superposición de vivo y muerto porque es un sistema macroscópico que puede medir su propio estado (colapsándolo). El mismo problema aparece en el nuevo experimento mental de Frauchiger y Renner, que introduce cuatro observadores (dos Wigner y dos amigos), para evitar (sin éxito) este problema. Como pasa muchas veces, complicar el álgebra y el razonamiento para esconder bajo la alfombra el problema no evita que el problema siga estando. A pesar de que los revisores del artículo lo acepten como válido tras la revisión por pares. Recuerda, que un artículo esté publicado en una revista con revisión por pares no significa que sea correcto; solo significa que los revisores creyeron que lo era.
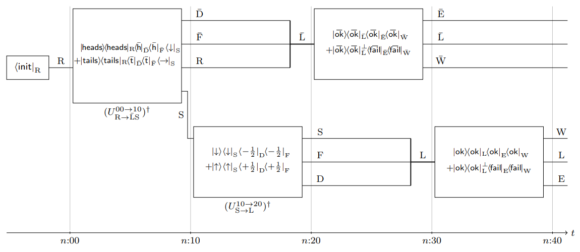
Este esquema muestra el experimento mental de Frauchiger y Renner en forma de circuito. Una discusión detallada alargaría mucho esta entrada, sin justificación aparente. Los interesados pueden seguir paso a paso el razonamiento del artículo original. Pero deben estar atentos a los lugares donde se realizan medidas y anotar en una hoja de papel aparte el resultado correcto según la mecánica cuántica, que no es el que aparece en el artículo. Así encontrarán que al complicar el experimento lo único que se hace es esconder bajo la alfombra el problema.

Como sé que muchos lectores van a protestar, porque esperan una discusión detallada por mi parte, me limitaré a discutir en detalle solo la primera conclusión de la tabla 3 del artículo. El problema es similar en las tres restantes. El observador mide
en el instante
, de lo que concluye que con seguridad
observará
en el instante
”. Frauchiger y Renner asumen que el observador
está dentro de un laboratorio aislado y que su medida (al ser ignorada por los demás agentes) se puede describir por una transformación unitaria (sin colapso). En dicho caso el estado del laboratorio
en el instante
será o bien
, o bien
, dependiendo del resultado de la medida de
. Por tanto, no es cierto que
observará siempre
; este resultado solo ocurrirá con una probabilidad de o bien
, o bien
, respectivamente.
La predicción que los autores del artículo escriben en la tabla 3 requiere asumir que la medida de produce el colapso del estado del laboratorio, lo que contradice la hipótesis de que ha sido realizada mediante una transformación unitaria. En dicho caso, el estado en el instante
estará dado por
, de forma independiente del resultado de la medida de
, con lo que
observará siempre
. Pero en dicho caso
nunca observará
, y la contradicción deseada por los autores nunca aparecerá.

El análisis del resto de las predicciones de los autores que aparecen en la tabla 3 es similar. Animo al lector interesado a realizarlo con cuidado. Por tanto, la supuesta demostración del teorema de incoherencia («ni de coña» como dice Héctor en el podcast) es incorrecta. Las hipótesis (Q), (C) y (S) del artículo no son contradictorias entre sí (cuando se usa la mecánica cuántica que todo el mundo estudia durante su carrera de Física).

Y para acabar, dicho lo dicho, no tiene sentido discutir qué interpretación de la mecánica cuántica describe mejor la realidad a la vista de un teorema de incoherencia que es incorrecto. Lo interesante de este tipo de artículo es que son un ejercicio ideal para los estudiantes de cursos de física cuántica en la carrera de Física. Animo a todos los profesores a discutirlo en clase y a solicitar a sus alumnos un informe detallado de los errores. Muchas veces la mejor manera de aprender es estudiar en detalle los razonamientos complicados que son capaces de confundir hasta a algunos expertos.


Hola Francis, solo soy un aficionado pero creo que puedo aportar algo.
Yo he estudiado el grado en Física y mi TFG ha ido sobre decoherencia, y por lo que he visto, en los pocos casos en los que se puede estudiar en detalle la interacción entre un cubit y un sistema macroscópico, https://arxiv.org/abs/quant-ph/9702001 por poner un ejemplo, la decoherencia hace que los efectos cuanticos desaparezcan, es decir, el sistema se comporta como si hubiera colapsado, y eso que en estos casos el sistema macroscópico es un gas de bosones, máxime, cuando se trate de un observador.
Perdón por el OFF-TOPIC: ¿Habéis visto el cambio de nombre de la Ley de Hubble?
Por recomendación de la Unión Astronómica Internacional, a partir de ahora se debe nombrar a la ley de expansión del Universo como LEY DE HUBBLE-LEMAÎTRE
Los detalles en castellano de los motivos y la gestación del cambio de nombre se pueden leer en:
http://forum.lawebdefisica.com/threads/41527-Renaming-the-Hubble-Law-Propuesta-de-cambio-de-nombre-de-la-Ley-de-Hubble
Saludos.
En primer lugar felicitar a Francisco por el magnifico trabajo de divulgación cientifica que realiza. Nunca he participado, pero el anterior comentariio me ha llegado al alma…
Me parece un gran acierto incluir el nombre de Lemaitre en la ley de expansion del universo. De hecho creo que cuando desarrolló su modelo cosmologico se apoyo en datos sobre corrimiento hacia el rojo aportados por otros astronomos. En mi opinión creo que se ha sobre valorado la figura de Hubble
A mi lo que me gustaría entender, qué es eso de medir el estado cuántico de un amigo + laboratorio + qubit…le veo tanto sentido como medir el spin de un balón de fútbol…ni pies ni cabeza… Cada día me siento más tonto
Hola Francis
En argentina hay un grupo de filosofía de la ciencia en la facultad de ciencias exactas y naturales de la Universidad de Buenos Aires, dirigido por la doctora en filosofía Olimpia Lombardi que investiga en la interpretación Modal de la mecánica cuántica, según te escuche a vos y te leí, vos pensas que no es necesaria ninguna interpretación meta física o filosófica, que con la misma física alcanza
Que pensas de la Modal interpretations ?
http://www.filoexactas.exactas.uba.ar/index.htm
Mientras escuchaba el poscast pensaba ¿Que opinaría Francis de todo esto? Gracias por la respuesta 🙂
Cuan cierto. Yo he de confesar que si no está Francis, en temas peliagudos, me quedo siempre con mucha desconfianza, y la razón es muy sencilla, cuando Francis abre la boca, todo coge sentido.
De hecho, si hay cuántica o IA, y no está Francis, como no vayan a entrevistar a un grande, ni me molesto en escucharlo.
En tu post indicas que el problema está en describir el resultado de una medida como una superposición. Es interesante añadir que, como se muestra en la referencia que aportas (https://arxiv.org/pdf/1810.06858.pdf) uno también puede demostrar que la inconsistencia no existe incluso si somos «many wolders» y consideramos que el proceso de medida es, de hecho, unitario.
Mis saludos, pese a que ha pasado cierto tiempo y no sé si escribirte aquí te notifique. ¿Crees que puedas ofrecer un análisis respecto a una prueba experimental del amigo de Wigner en una próxima nota en tu blog? Los detalles del experimento y sus conclusiones se encuentran en: Experimental rejection of observer-independence in the quantum world, Massimiliano Proietti (et. al) [ https://arxiv.org/abs/1902.05080 ]. No conozco hasta ahora críticas, sólo citaciones en algunos trabajos (v. gr. https://arxiv.org/abs/1805.05774v10 y https://arxiv.org/abs/1901.01841). Te agradezco de antemano.
Robertt, ya hablé de dicho artículo en «Los «hechos» en mecánica cuántica dependen del observador» LCMF 05 mar 2019: https://francis.naukas.com/2019/03/05/los-hechos-en-mecanica-cuantica-dependen-del-observador/
Ah, mil disculpas. Gracias por dejarme al tanto.