El límite clásico de una teoría cuántica de la gravedad permite calcular correcciones a las teorías de Newton y Einstein para la gravedad a escala macroscópica. La corrección más sencilla explica la materia oscura y minimiza los efectos de la energía oscura. Así lo ha demostrado Alexandre Deur utilizando simulaciones de Montecarlo para resolver la interacción gravitón-gravitón utilizando la aproximación de campo débil. Un resultado sorprendente que ha recibido poca atención por parte de los especialistas, quizás por estar publicado en Physics Letters B en lugar de en Physical Review Letters. El artículo técnico es A. Deur, «Implications of graviton–graviton interaction to dark matter,» PLB 676: 21-24, 1 June 2009 (ArXiv version). Por cierto, por si no lo sabes, muchos (yo me incluyo) de los que envían artículos a PRL si reciben un rechazo los envían a PLA o PLB donde normalmente se publican mucho más fácilmente.
Como la constante de acomplamiento de la gravedad es muy pequeña (porque la gravedad es una fuerza muy débil) uno espera que las correcciones de segundo orden serán extremadamente pequeñas. Pero no es así. De hecho, en una teoría cuántica de la gravedad son las responsables de la corrección de la fuerza inversa al cuadrado de Newton introducida por la teoría de Einstein, que explica el corrimiento del perihelio de Mercurio. De hecho, entre dos masas el potencial gravitatorio queda como . Este cálculo requiere que la gravedad sea débil ya que en el caso de que sea fuerte el resultado diverge (es infinito).
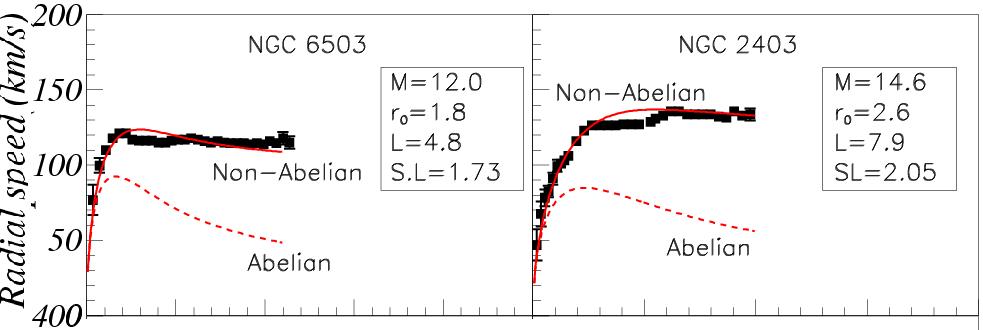
¿Cómo afectarán las correcciones cuánticas al comportamiento de galaxias? Deur las llama correcciones «no abelianas» versus a las correcciones «abelianas» que habían sido consideradas previamente, parafraseando a la cromodinámica cuántica versus la electrodinámica cuántica. Estas correcciones hay que calcularlas utilizando métodos numéricos aplicados a la expansión de la acción de Einstein-Hilbert en serie de potencias en función del acoplamiento. Si la distribución de masa es perfectamente esférica, estas correcciones son muy pequeñas. Pero cuando la distribución de masa es anisotrópica (como en una galaxia, básicamente plana) pueden ser importantes. El resultado numérico para evaluar el propagador de Feynman (función de Green) a utilizar en los diagramas de Feynman entre gravitones presenta un término nuevo, de tipo logarítmico.
La figura que abre esta entradaa es uno de los 6 ejemplos de curvas de velocidad radial de estrellas en galaxias en función de su radio y muestra el buen acuerdo entre la nueva teoría y los resultados experimentales. También se observa buen acuerdo en el caso de galaxias enanas (figura 4 del artículo). Muy interesante es el hecho de que la nueva teoría permite explicar la relación experimental de Tully-Fisher (hasta ahora sin explicación teórica en el modelo de materia oscura basado en partículas elementales supersimétricas y difícil de explicar en otras teorías como MOND).
La nueva teoría predice nuevos resultados que podrán ser verificados/refutados experimentalmente: (1) las curvas de velocidad estelar para galaxias esféricas serán más próximas a las curvas newtonianas que para galaxias elípticas; (2) dos galaxias espirales interactuarán más débilmente que dos galaxias esféricas; (3) el potencial gravitatoria se volverá aproximadamente lineal en clústeres de galaxias ralos; y (4) los modelos de formación galáctica, que actualmente utilizan y requieren materia oscura, conducirán a resultados ligeramente diferentes con la nueva teoría.
¿Cómo afecta el nuevo resultado a la energía oscura? Como el universo está en expansión, la diferencia entre la fuerza gravitatoria «no abeliana» y la usual («abeliana») se puede interpretar como un efecto gravitatorio repulsivo, que sería responsable de gran parte de la aceleración del universo actualmente observada en los experimentos con supernovas tipo Ia. La nueva teoría no parece explicar toda la energía oscura pero si reduce enormemente su valor para explicar la aceleración actual de la expansión del universo.
Cuando un artículo ofrece una explicación sencilla (la interacción gravitón-gravitón) para explicar hechos experimentales como la materia oscura y la energía oscura uno ha de quitarse el sombrero. Un gran trabajo de Deur, sin lugar a dudas. Al final, si se confirma esta nueva explicación, una de las grandes utilidades del LHC del CERN, encontrar las partículas de materia oscura se puede quedar en agua de borrajas.
PS (26 junio 2009): Es curioso que nadie haya hecho el comentario que yo esperaba. Pero ¿hay una teoría cuántica de la gravedad? La respuesta es sencilla. Sí la hay. Aplicar la mecánica cuántica a la gravedad es fácil y ya lo hizo hace muchos años Bryce S. DeWitt. El problema es que la teoría resultante no es aplicable a la escala de Planck (donde todo el mundo espera que sea aplicable) porque allí aparecen ciertos «grandes» problemas técnicos. Pero para escalas muy inferiores a la de Planck, la teoría cuántica de la gravedad es perfectamente consistente. Los interesados en más detalles pueden consultar, por ejemplo, A. Strominger, «Is there a Quantum Theory of Gravity?,» in «Quantum Theory of Gravity: Essays in honor of the 60th birthday of Bryce S. DeWitt,» edited by Bryce S. DeWitt, Published by Adam Hilger Ltd., Bristol, England, 1984., p.210 (los interesados podrán localizar una copia pirata de dicho libro fácilmente).


El tiempo dirá sobre esta nueva forma de calcular la gravedad. En mi esquema conceptual, desde hace muchos años, vengo contando con un espacio vibratorio en expansión que da la energía a toda la materia.Creo que convendría replantear determinados cálculos en los que se podría postular que esta energía mueve el Universo material. A mi, de este modo, me salen los cálculos y la coherencia con los hechos. Por ejemplo, en este caso, la fórmula principal es e = m.W (energía igual a masa por la fuerza expansiva del Universo), y de esta fórmula, sin necesidad de coger el bolígrafo, se deducen f = m.a (de Newton) y e = m.c2 (de Einstein).
Saludos. Ramon Marquès
This is indeed my favorite theory for dark matter. Also, notice that the non abelian approximation could well explain that the web of dark matter that links galaxy clusters are analogs to gluon flux tubes from QCD
¿Escalas muy inferiores a la de Plank? ¿No será «superiores»?
Waldemar, sin matemáticas estas cosas nunca se explican bien. Si es escala de energía o masa, es inferior. Si es escala de espacio o tiempo, es mayor.