Una amiga, lectora de este blog, me comentó hace casi diez años que por qué no me dedicaba a resolver el problema del milenio sobre la regularidad de las soluciones de las ecuaciones de Navier-Stokes. Obviamente es imposible que con mis parcos conocimientos en matemáticas puras pudiera lograrlo. En 2006 le comenté a pie de pasillo que una mujer matemática, Penny Smith, tras 30 años de investigación, podría haber resuelto dicho problema. Más tarde se descubrió que había un error en su demostración. Retractó su artículo. El artículo era Penny Smith, «Immortal Smooth Solution of the Three Space Dimensional Navier-Stokes System,» ArXiv, Submitted on 26 Sep 2006, secuela de «Eternal Continuous Viscosity Solutions of the Einstein Cauchy Problem,» ArXiv, Submitted on 13 May 2006 (ambos artículos retractados en 8 Oct 2006; el segundo contiene un error propagado al primero). ¿Un buen momento para recordar su historia? ¿Y por qué no? Nos cuentan muchos detalles de esta historia tanto Peter Woit, «Navier-Stokes Equation Progress?,» Not Even Wrong, October 5th, 2006, como Jenny Hogan, «Has famous maths problem been solved, and in only a month? Has $1 million maths problem been cracked using novel techniques?,» Nature, News, 9 October 2006. Los interesados en los detalles de la demostración disfrutarán con Brooks Moses, «Penny Smith’s Proof on the Navier-Stokes Equations,» Brooks Moses: Notes on Divergent Simulations, 10 June 2006.
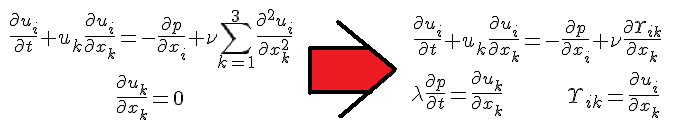
Penelope (Penny) Smith, de la Lehigh University, en Bethlehem, Pennsylvania, EEUU, envió un artículo al servidor ArXiv y a la revista Journal of Mathematical Analysis and Applications proponiendo una solución a uno de los problemas del milenio del Instituto Clay de Matemáticas, dotado con un premio de un millón de dólares. Creyó haber demostrado que existe una solución suave eterna (que no explota o produce singularidades en tiempo finito) de las ecuaciones de Navier-Stokes en 3 dimensiones. La idea de la demostración era escribir estas ecuaciones como el límite en un un sistema hiperbólico cuasilineal cuando cierto parámetro tendía a cero. Este tipo de problemas encajaba en el marco teórico que ella misma había publicado con anterioridad y sólo bastaba demostrar que el límite existía, lo que le requirió sólo 9 páginas en su preprint. Sus artículos anteriores eran Penelope Smith, «Perron’s method for quasilinear hyperbolic systems: Part I,» Journal of Mathematical Analysis and Applications 316: 357-368, 1 April 2006, y «Perron’s method for quasilinear hyperbolic systems, Part II,» JMAA 316: 483-494, 15 April 2006 (ver también «Corrigendum to “Perron’s method for quasilinear hyperbolic systems, Part II” [J. Math. Anal. Appl. 316 (2006) 483–494],» JMAA 329: 1484, 15 May 2007).
La polémica con el trabajo de Smith comenzó pronto. Por un lado, afirmaba que sólo necesitó un mes para su demostración (basada en su trabajo previo de 30 años). Por otro lado, su artículo sólo tenía 9 páginas y se basaba mucho en sus artículos anteriores, algunos de los cuales no estaban en ArXiv y no se podían leer (aunque estaban aceptados para publicación en JMAA). Más aún, Penny recibió ofertas de trabajo, por ejemplo, del prestigioso Institute for Advanced Study en Princeton, EEUU. Y la gente ya se sabe que es envidiosa.
Penny Smith lo pasó mal. Muchas voces clamaron en su contra. «I can mostly fix the paper (except for Navier Stokes) if people would stop beating me up for makeing a subtle error. It is not as if I have been dishonest. […] Please don’t beat the shit out of me.» Ella tuvo que recordar sus grandes éxitos «My first paper solved a major problem in compressible gas dynamics including three dimensions. My second Paper gave a smooth family of transonic flows in a plane exterior problem disproving a famous and incorrect theorem.» Bueno, no hay que exagerar, que estos primeros artículos de Penny prácticamente no han sido citados, luego tan importantes no serán («According to Mathscinet, during 1982–2006 Penelope Smith has published 18 papers which were cited 11 times by 8 authors«). Estos extractos están sacados de los comentarios del artículo de Woit en Not Even Wrong. Penny era habitual lectora y comentadora en dicho blog (ahora no sé si seguirá siéndolo).
Penelope tuvo que recordarnos que «Doing mathematics is 99.9% grueling labor and approximately 0.1% brilliant ideas.»
El error en el artículo de Penny era sutil, muy sutil, extremadamente sutil… no se encontraba en el propio artículo. ¿Dónde entonces? Se encontraba en su preprint anterior sobre el problema de Cauchy de las ecuaciones de Einstein. El teorema 4 de dicho artículo contenía un error (según Penny, muy sutil) a la hora de extender la validez de un teorema de comparación de soluciones de un espacio en el que es difícil demostrarlo a otro en el que ahora resulta claro que es imposible lograrlo (hay un contraeejemplo). Sin dicho teorema, el trabajo de Penny sobre las ecuaciones de Einstein y Navier-Stokes se cae por su propio peso.
Penny sigue trabajando, como buena matemática, como buena hormiguita, poquito a poco, publicando sus cositas.

