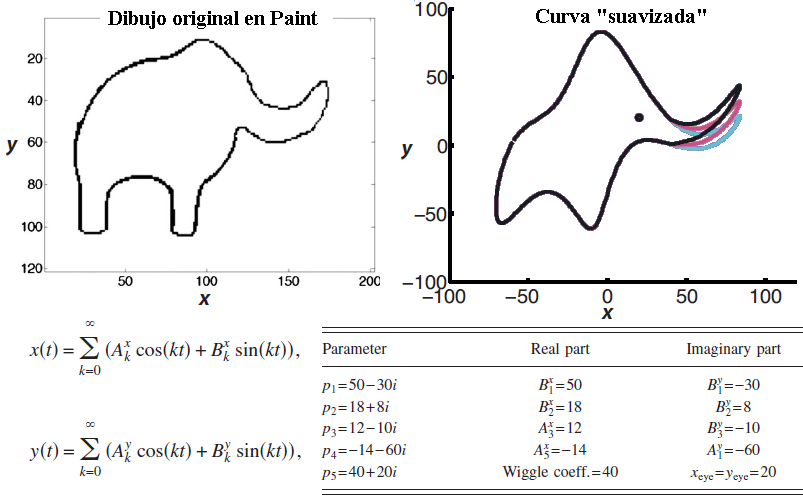
John von Neumann afirmó: «con cuatro parámetros puedo ajustar un elefante, y con cinco puedo lograr que mueva su trompa.» Enrico Fermi le recordó esta frase a Freeman Dyson en una conferencia en 1953 y desde entonces es ampliamente conocida entre los físicos. ¿Cómo se puede ajustar con sólo cuatro números una curva cerrada con forma de elefante? Muy fácil, se ajustan las dos componentes (x(t),y(t)) de la curva con una serie de Fourier y truncamos esta serie de tal forma que obtenemos una aproximación «suavizada» de la curva original (en la que hemos eliminado las altas frecuencias). Jugando un poquito es fácil obtener figuras realmente complicadas con sólo unos pocos números. Con cuatro números reales es difícil obtener algo que se parezca a un elefante, pero con cuatro números complejos es realmente fácil. La figura que abre esta entrada muestra un ejemplo, incluyendo la serie de Fourier y los 4 parámetros complejos necesarios. La parte real del quinto parámetro permite mover la trompa del elefante. Este tipo de técnica es ampliamente utilizada en el Reconocimiento de Imágenes utilizando contornos (a los contornos activos se les suele llamar snakes), aún así, me parece que a veces hay que recordar incluso lo ampliamente conocido. Una curiosidad que nos cuentan Jürgen Mayer, Khaled Khairy y Jonathon Howard en «Drawing an elephant with four complex parameters,» Notes and Discussions, American Journal of Physics 78: 648-649, June 2010.
9 Comentarios
Deja un comentario
Por Francisco R. Villatoro, publicado el 27 mayo, 2010
Categoría(s): Ciencia • Informática • Matemáticas • Mathematics • Science
Etiqueta(s): Ciencia, Curiosidades, Matemáticas
⇦ Publicado en Nature: Imagen por radar de la topografía transversal del gran cañón del casquete polar marciano • Publicado en Science: Pendientes para la oreja utilizados como pasaportes entre Mesopotamia y la India en el III Milenio A.C. ⇨
Categoría(s): Ciencia • Informática • Matemáticas • Mathematics • Science
Etiqueta(s): Ciencia, Curiosidades, Matemáticas
⇦ Publicado en Nature: Imagen por radar de la topografía transversal del gran cañón del casquete polar marciano • Publicado en Science: Pendientes para la oreja utilizados como pasaportes entre Mesopotamia y la India en el III Milenio A.C. ⇨


Hola, esto demuestra que todo está ahí, que sólo hay que saber cómo y dónde buscarlo.
Buena… a ver cuanto se demora la masa en hacer un falo
Es la famosa fórmula de Arthur-Gus:
f(X) = A · |cos(X) – B|
donde:
A : Factor de elongación
B : Factor de proporción [0,1]
k show we la neta esta chido ta padre karnal la neta asi komo kompa te felicito por tu trabajo tio t kiero tio bye t kiero un buen tio rekuerda k diosesito t protege siempore tambien el kompa san pedro bye tio t kiero haci haci de mucho tio bye tio
Esto pal veranito me enseñais a hacerlo vale?
esto pal veranito me enseñareis a hacerlo vale?
salu2
>>Josealfredoauditore
amigo, aca hablamos español
«con cinco puedo lograr que mueva su trompa»: eso si que sería un puntazo, que me moviera la trompa.
Eso es una familia de soluciones-elefante. Con un punto mas, podrías determinar si es asiático o africano.
saludos!