Los sistemas de fermiones pesados que son superconductores presentan al menos dos fases superconductoras que coexisten a baja temperatura. Según la variante de la teoría BCS que se aplica a estos sistemas se debe violar la simetría de inversión temporal. Se publica en Science la primera observación experimental de esta violación en un cristal de UPt3 gracias al efecto Kerr polar. La reflexión de luz polarizada circularmente a la derecha o a la izquierda que incide en la dirección normal sobre un cristal de UPt3 presenta un desplazamiento en fase que es una señal inequívoca de la violación de la simetría de inversión temporal. El resultado confirma la teoría BCS aplicada a este superconductor exótico, en contra de otras teorías alternativas.
Nos lo cuenta Dirk van der Marel, George Albert Sawatzky, «An optical twist for triplet superconductors,» Science 345: 138-139, 11 Jul 2014. El artículo técnico es E. R. Schemm et al., «Observation of broken time-reversal symmetry in the heavy-fermion superconductor UPt3,» Science 345: 190-193, 11 Jul 2014.
Los sistemas de fermiones pesados son compuestos metálicos y aleaciones que contienen iones 4f o 5f (como Ce, Pr, Yb o U) cuyos electrones de conducción se comportan como cuasipartículas con una masa efectiva muy grande por debajo de la temperatura crítica de Kondo (10 Kelvin en UPt3). Muchos sistemas de fermiones pesados presentan una transición de fase hacia un estado superconductor en el que los pares de Cooper corresponden a pares de fermiones pesados en lugar de pares de electrones. Por ello, la superconductividad en estos materiales no es la convencional, el parámetro de orden superconductor es complejo y describe los grados de libertad internos de los pares de Cooper. El superconductor de fermiones pesados más conocidos es UPt3.
La teoría BCS (por Bardeen-Cooper-Schrieffer) de la superconductividad se aplica a superconductores cuyos iones están en un estado electrónico sin momento angular (estado s, también llamado onda-s). Dicha teoría se puede generalizar a iones con momento angular no nulo (estados p, d o f, también llamados onda-p, onda-d y onda-f), como mostraron P. W. Anderson y P. Morel «Generalized Bardeen-Cooper-Schrieffer States and the proposed low-temperature phases of 3 He,» Phys. Rev. 123: 1911, 1961. En 1972 se descubrió la superfluidez en 3He, cuyos estados tipo onda-p presentan una rotura de la simetría de inversión temporal. En 1979 se descubrió el análogo metálico a la superfluidez en 3He en los superconductores de fermiones pesados. Según la teoría estos superconductores exóticos también deben mostrar la rotura de la simetría de inversión temporal.
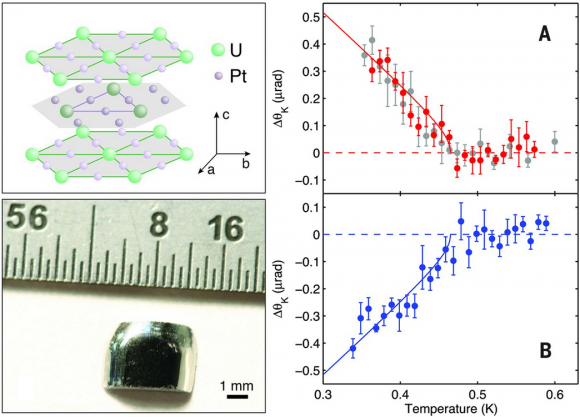
La superconductividad de UPt3 fue descubierta en 1984, con una temperatura de transición Tc ~526 mK. Se descubrió que presenta dos fases superconductoras con temperaturas de transición Tc=Tc+ y Tc− separadas ~50 mK. Como el estado supercondutor de un sistema de fermiones pesados depende de los estados electrónicos de tipo cuasipartícula, sus propiedades dependen de su estructura cristalina. La estructura cristalina de UPt3 es el grupo puntual D6h (6|mmm). Las dos fases superconductoras tienen su origen en la paridad de las representaciones del grupo Dh6. Según la teoría BCS modificada las representaciones de paridad par (E1g y E2g) y de paridad impar (E1u y E2u) dan lugar a cuasipartículas que se acoplan de forma diferente para formar dos tipos de pares de Cooper que se condensan en dos dos fases superconductoras con temperatura de transición próxima. Además, la existencia de estas dos fases permite, según la teoría, que el parámetro de orden superconductor sea complejo en lugar de real, con lo que se observa una violación de la simetría de inversión temporal. Sin embargo, se han descrito variantes de esta teoría que permiten que el parámetro de orden sera real, con lo que esta simetría se preserva. En esta situación, la última palabra la tiene el experimento.
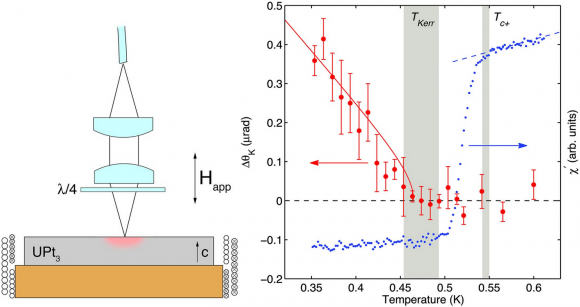
La respuesta ante luz incidente polarizada de los dos estados superconductores es diferente si se viola la simetría de inversión temporal. Aparece una diferencia de fase que puede ser medida experimentalmente. En el cristal utilizado en el nuevo artículo se tiene Tc+ = 553 mK (±2 mK) y se ha ajustado el láser para medir el efecto Kerr polar a una temperatura TKerr ~ 460 mK ~ Tc–.
Al incidir la luz polarizada dos electrones en un átomo de uranio pasan a un nivel atómico 5f con una energía U+J si forman un estado singlete con espín igual a cero y U−J si forman un estado triplete con espín igual a uno, donde U es la interacción eléctrica Coulombiana entre los dos electrones que ocupan el estado 5f y J es la interacción de intercambio según la regla de Hund. Para U < J el resultado es una interacción atractiva entre ambos electrones, que se pueden hibridar dentro del mismo átomo de uranio si sus espines son paralelos. Cuando sus espines son antiparalelos la interacción mutua es repulsiva.
El coeficiente de absorción de luz polarizada circulamente a izquierdas o a derechas depende del momento angular total del par de electrones en el estado 5f. Como la luz con polarización lineal es una superposición de fotones con polarización circular a izquierda y a derechas, la absorción diferencial en ambos casos produce una rotación del ángulo de polarización de la luz. Este resultado ha sido observado y confirma la violación de la simetría temporal en el superconductor UPt3. Además, sugiere que esta violación también ocurre en los demás sistemas de fermiones pesados que son superconductores exóticos.
[PARA USUARIOS DE MENEAME] Esta entrada ha sido portada en este agregador de noticias y todos los comentarios parecen indicar que nadie ha entendido qué es lo que se ha logrado. Voy a tratar de explicar ¿qué es un superconductor? ¿qué es la teoría BCS? ¿qué relación tiene con la simetría de inversión temporal?
Los materiales que conducen la electricidad a temperatura ambiente (como los metales) tienen resistencia eléctrica. En 1911, H. Kammerlingh Onnes descubrió que el mercurio (Hg) por debajo de 4,1K conduce la electricidad sin resistencia eléctrica. Hay varios tipos de superconductores. Los superconductores de tipo I, como el mercurio y otros 29 metales puros, son superconductores por debajo de cierta temperatura crítica y por debajo de cierto campo magnético crítico. Presentan el efecto Meissner, que impide que un campo magnético pueda penetrar en su interior. Su utilidad práctica es limitada porque no soportan campos magnéticos intensos.
En 1930 se descubrió que ciertas aleaciones son superconductoras (como niobio-titanio, NbTi, cuya temperatura de transición es 10 K y cuyo campo magnético crítico son 15 T). Se llaman superconductores de tipo II y soportan campos magnéticos mucho más intensos, por lo que tienen muchas aplicaciones en la construcción de imanes (como los del LHC en el CERN). Por debajo de la temperatura crítica, estos superconductores presentan dos estados simultáneos, uno normal y otro superconductor. En 1986 se descubrió que algunos cupratos (compuestos de cobre) son superconductores a alta temperatura (el récord son 243 K) y en 2008 se hizo lo propio con los pnicturos (compuestos de hierro). Hay muchos tipos de superconductores que presentan propiedades diferentes.
¿Por qué un material se vuelve superconductor a baja temperatura? John Bardeen, Leon Cooper y Robert Schrieffer descubrieron en 1957 una teoría que explica perfectamente el comportamiento de los superconductores de tipo I y lograron el Premio Nobel en 1972. La teoría BCS (por Bardeen-Cooper-Schrieffer) afirma que los electrones forman parejas (pares de Cooper) gracias a su interacción con la red cristalina. En lenguaje cuántico, los electrones intercambian fonones. Recomiendo leer una explicación sencilla en Enrique Borja, «Cooper, con un par,» Cuentos Cuánticos, 26 Abr 2013.
La idea básica es un electrón en movimiento atrae a los átomos de la red cristalina, originando una onda en su dirección de movimiento que atrae a otro electrón que se mueve en dirección opuesta. Esto provoca una interacción de largo alcanza (unos 100 nm) entre ambos electrones mediada por las ondas en la red cristalina. En una diagrama de Feynman, ambos electrones interaccionan vía un fonón (vibración elemental de la red cristalina).
Los electrones son fermiones, cumplen el principio de exclusión de Pauli, pero los pares de Cooper son bosones y a baja temperatura forman un estado condensado de Bose-Einstein (todos los pares de Cooper se comportan como un «macro-átomo» con un estado cuántico común a todos ellos). Este estado cuántico macroscópico es el responsable de la superconductividad.
¿Cómo influye la configuración electrónica en los iones de la red? Por el principio de exclusión de Pauli, los electrones se colocan en capas u orbitales (configuración electrónica) alrededor de los núcleos. Estos orbitales están descritos por tres números cuánticos: el principal (n), el azimutal (l) y el magnético (m). El azimutal se representa por las letras s (0), p (1), d (2) y f (3). Las ondas que se producen en la red cristalina según la teoría BCS dependen de este número y los superconductores se clasifican en tipo onda-s, onda-p, onda-d y onda-f. La supeconductores de tipo I son tipo onda-s. La mayoría de los superconductores de alta temperatura son tipo onda-d.
La diferencia entre los orbitales s, p, d y f es el momento angular del ión (que determina el momento angular del fonón que media la interacción entre los electrones del par de Cooper). Los orbitales s son «esféricos» y por tanto respetan la simetría rotacional. Sin embargo, los demás tipos de orbitales no lo son y la simetría rotacional está rota.
La teoría BCS aplicada a iones con momento angular, superconductores tipo onda-p, onda-d y onda-f, fue desarrollada (como indico más arriba) por Anderson y Morel en 1961. Sin embargo, no explica los superconductores de alta temperatura. Aún así, predice fenómenos muy interesantes, como la violación de la simetría de inversión temporal para superconductores tipo onda-f. Fenómeno que ha sido verificado por primera vez en un experimento y motivo de la noticia de esta entrada.
¿Qué tiene que ver todo esto con la inversión temporal? Cuando los pares de Cooper están formados por electrones, siempre se cumple la simetría de inversión temporal. En un sólido conductor los electrones viajan casi de forma libre por todo el cristal y ocupan estados fermiónicos. Para un valor del impulso p hay dos posibles estados electrónicos, uno con la componente z del momento angular de espín positiva y otro negativa. Cuando se tiene simetría de inversión temporal, la energía de estos electrones respecto a su impulso tiene la propiedad Ep = E–p, por cada electrón en un estado con energía Ep tenemos otro de la misma energía pero impulso y momento magnético en sentido contrario.
Sin embargo, en un sólido conductor puede haber estados de muchos electrones que se comportan de forma colectiva como si fueran una sola partícula, llamados cuasipartículas. Estas cuasipartículas pueden comportarse como bosones (si como los pares de Cooper tienen un número par de electrones) o como fermiones (si tienen un número impar). En este último caso, la teoría BCS permite la aparición de «pares de Cooper» formados por pares de cuasipartículas.
Estas cuasipartículas son fermiones, pero sus propiedades, como es obvio, no son idénticas a las de los electrones. En los llamados «sistemas de fermiones de pesados» se comportan como «electrones» de gran masa (fermiones pesados). En estos materiales se pueden formar pares de Cooper. Al tratarse de cuasipartículas, sus estados pueden violar la simetría de inversión temporal, es decir, puede ocurrir que la energía de las dos cuasipartículas que forman un par de Cooper no sea exactamente idéntica (recuerda una cuasipartícula deforma la red cristalina y la otra siente dicho efecto al pasar en dirección opuesta por dicha región). En este caso se viola la simetría de inversión temporal.



Si quieres divulgar, ponte al nivel de tus potenciales lectores; no escribas artículos que sólo tu mismo eres capaz de entender. No he entendido nada pese a que estoy seguro de que es un artículo correctísimo. Como no expliques las cosas con flores y abejas el 99,999% de la gente que acabe aquí no se va a enterar.
José Luís, es que se supone que Francis hace las entradas pensando en estudiantes de universidad y profesores. Por eso al lector que busca simple divulgación ciertas entradas (como esta) le costarán mucho comprender.
José Luis, mi objetivo es motivar a profundizar. Si te interesa el asunto, en mi entrada tienes las palabras clave, profundiza en la web y disfruta aprendiendo. Quien quiera que le cuenten con flores y abejas los últimos resultados sobre superconductores tendrá que buscar en otro lugar. La ventaja de haber pasado primero por aquí es que sabrá qué palabras clave buscar y las sabrá el mismo día en el que se ha publicado el nuevo avance.
Saludos
Francis
José, mira este otro blog, te resultará más accesible:
http://www.thespectrumofriemannium.com/2012/11/07/log050-why-riemannium/#point1
Por cierto, el segundo de los homenajeados en esa dedicatoria… pues como que ya tienes el gusto.
Y sí, lo de «más accesible» era una ironía… relativa. ¿Sabes la última? No lo comentes en voz alta, pero… dicen (repito: dicen) que también hay blogs de abogados para abogados. ¡Horror!
Divulgar no tiene por qué significar que lo tiene que entender un niño de 4 años o una persona sin formación específica. Eso es una parte tan solo, importante, muy importante, pero no todo.
Hay cosas que son imposibles de explicar a gente sin una formación básica sin destrozar por completo el sentido de lo que se pretende explicar. La ciencia es una montaña enorme que se construye con el esfuerzo de mucha gente y para entender lo que pasa en las partes más altas hay que escalar. No queda otra.
No todo se puede explicar con abejitas. El problema de la divulgación es que implica traducir un lenguaje riguroso y sistemático en un lenguaje impreciso y eso si se abusa, acaba perdiendo toda rigurosidad y conexión con la realidad. Y así pasa, que hay mucha divulgación por ahí de conceptos avanzados que lo único que hacen es hacer daño y confundir más todavía.
Y todo tiene cabida: divulgación para todos los públicos y divulgación especializada. No pasa nada.
Totalmente de acuerdo. No hay quien lo entienda. Ahora, si lo que quiere es crear un blog para físicos cuánticos y demás, pues adelante.
Hola José Luis, un consejo por si quieres entender las notas sobre nuevos temas que te interesen aunque te abrumen o excedan: las lees igual. Verás que con el tiempo al leer otras tantas sobre el mismo tema y mismo nivel subrepticiamente comprenderás de que se trata el asunto. A mi me resulta. Salu2.
Francisco, si tu objetico es motivar a profundizar creo que estás muy lejos de conseguirlo. Te limitas a describir los resultados pero no motivas. No dices las implicaciones del estudio mas allá de «violar la simetría de la inversión temporal». ¿Qué es eso? ¿Qué implica? ¿Qué podríamos hacer con ello en un futuro? No sé,… pajas mentales que motiven al personal, que lo hagan soñar, que lo asombren, que lo ilusionen con las espectativas. Si te limitas únicamente a describir perfectísimamente (eso sí), tus artículos no serán mucho mas excitantes que una guía telefónica. Y todo esto te lo digo porque como principal objetivo de tu blog pones que es divulgar.
¿Y que hay de gente como yo que les interesa más este tipo de divulgación? A mi Francis sí me motiva a profundizar en ciertos temas. Lo que me vengo a referir es que de divulgación «básica» (que no requiere conocimientos especializados) hay un montón, pero especializada hay poca (o al menos a mí me cuesta mucho encontrarla tan bien explicada).
Yo creo que ha de haber de todo. Así, todos contentos. Es que no pensáis en que sí hay gente que le gustan las cosas explicadas así. ¿Queréis entonces que para nosotros no haya este tipo de divulgación?
Con todos mis respetos, sois un poco pesados con el tema del nivel y la dificultad. Os basáis en que todo lo que se publica se tiene que escribir específicamente para vosotros y por eso os quejáis.
La divulgación tiene, y debe tener, muchos niveles. Tiene que haber libros de ciencia para niños, para gente no científica pero con un cierto nivel cultural, para científicos de otros campos, para científicos del mismo campo y un largo etcétera. El hecho de que Francis dedique algo de su tiempo a seleccionar y resumir publicaciones recientes nos viene muy bien a muchos, que pasamos por aquí para echar un ojo a lo que se está haciendo. Si el nivel es demasiado alto para algunos es tan fácil como irse a otras entradas, a otros blogs, o a un libro de divulgación, pero no intentéis quitarnos esto a los demás.
En primer lugar, mi profunda admiración y agradecimiento a Francis (y al resto de colaboradores de este blog).
Y en segundo, mi comprensión a quienes se sienten abrumados (yo soy uno de ellos, si bien me gusta leer este tipo de artículos aun a sabiendas de que no entenderé el 99% de lo que se diga) por el nivel de los temas tratados. Esta sensación, al menos en mi caso, ha crecido desde que se han ido adhiriendo nuevos bloggeros a naukas (provenientes de otros blogs) y a priori casi nunca sé si el artículo es «accesible» a mi nivel o no. Estaba pensando en este sentido que quizás fuese útil un código cromático, algo similar a las pistas de esquí, para que los no iniciados estemos avisados al entrar al artículo.
En cualquier lugar, muchas gracias a todos por esta maravillosa labor de divulgación que realizáis que, como bien resaltaba un comentario anterior, se debe realizar a todos los niveles y no solo para los profanos (como soy yo).
Yo también agradezco a Francis este blog, cuya virtud es que va un poco más allá de la pura divulgación.
También reconozco que no siempre estoy al nivel (sobre todo en física de partículas) pero aún así me gusta que no todo sea divulgación para legos.
Una pregunta: Si no hay simetría de inversión temporal, significa que este sistema no conserva la energía¿?
Supongo que tu pregunta apunta hacia el Teorema de Noether que afirma que se conserva la energía siempre que el sistema sea invariante respecto de traslaciones temporales.
Pues no se responderte y estoy igual de intrigado que tú, (no soy físico, solo un aficionado que consulta esta página)
Creo entender que el Teorema de Noether se deduce de la formulación clásica de la física y por eso no sé si es aplicable a la mecánica cuántica. Por otro lado no estoy seguro que “traslación temporal” sea lo mismo que “rotura de la simetría de inversión temporal”
Ojalá el autor del blog o alguno de los físicos que lo visitan nos pueda sacar de dudas.
Pues no son lo mismo. La primera conserva energía, la segunda conserva paridad temporal:
http://en.wikipedia.org/wiki/Symmetry_(physics)#Conservation_laws_and_symmetry
¿Qué significa la rotura de la segunda? La respuesta en ENTRADAS RELACIONADAS:
https://francis.naukas.com/2009/12/22/la-violacion-de-la-simetria-t-de-inversion-temporal-y-el-origen-de-la-flecha-del-tiempo/
Saludos
Si leen inglés, aquí hay una respuesta buena:
physics.stackexchange.com/questions/44628/cpt-violation-and-symmetry-conservation-laws
En resumen, translaciones temporales no son lo mismo que inversión temporal. Translación temporal es una transformación continua, es decir, puedes tomar translaciones temporales cada vez más pequeñas hasta cero. Inversión temporal es una transformación discreta que da vuelta la flecha de tiempo, hacia adelante (+1, por ejemplo) o hacia atrás (-1). Son transformaciones de simetría diferentes, y la inversión temporal de hecho no es una simetría de la naturaleza.
Pues muchísimas gracias tanto a Andrés Guzmán como a Pelau
Porque la ironia? No era necesario lo de usuarios de meneame, jejeje. En terminos matematicos diria, que es muy dificil y tedioso, que cada vez que se quiera explicar una integral, una derivada, un teorema, una demostracion, tengamos que empezar diciendo: «La matematica es una ciencia que surgio por la necesidad del hombre de cuantificar las cosas, las 4 operaciones basicas son…….y bla bla bla», o lo que seria aun peor: «La primera letra del alfabeto es la A, la segunda es la B…..etc,etc» Existe bibliografia para todos los niveles y todas las carreras universitarias comenzaron en el Jardin de infantes para 3 años, sin embargo, en una clase de Optoelectronica, el temario no empieza con la lectura de Caperuzita y el lobo. Habra que sentar las baes necesarias para entender los articulos que aqui se publican, o de lo contrario no volver por aqui nunca si no se entiende lo escrito. Lo digo con total respeto y sin animo de ofender a nadie, pero si yo quisiera participar de un foro de fisioterapia, no pretenderia que me expliquen en ese lugar los puntos de insercion muscular del cuadriceps, porque eso deberia saberse desde anatomia de primer año. Saludos
¡Por supuesto que era necesario! 🙂 Los contra-argumentos están bien, pero los contra-ejemplos están mejor.
El estupendo blog de amarashiki es un ejemplo de nivel verdaderamente alto. Por contraste, el de Francis parece apto para todo público 😉
O sea: que dos blogs pueden ser igualmente excelentes y a la vez completamente distintos, según a qué potenciales lectores están orientados.
O sea del o sea: que hay divulgación para todos los gustos y niveles, incluyendo blogs de físicos para físicos.
¿Por qué usé la ironía? Por su nivel de contraste, precisamente. El humor es cosa seria.
¿Por qué dije que esa ironía era relativa? Porque su validez depende de los conocimientos y preferencias del lector. Yo carezco de base matemática y aun así logro seguir las asociaciones de conceptos con las que amarashiki «juega» de manera tan lúcida como amena.
¿Por qué tengo que ponerme a explicar todo esto? Porque, vaya casualidad, evidentemente se me fue la mano con el nivel del irony-o-meter 😀
Saludos.