La energía oscura es el gran misterio de la física del siglo XXI. La densidad de energía oscura coincide con la (probable) masa de los neutrinos. ¿Casualidad o causalidad? La física italiana Licia Verde (ICREA, Univ. Barcelona) y varios colegas proponen que la masa de los neutrinos depende del campo escalar responsable de la energía oscura. La masa de los neutrinos crece hasta que adquieren su masa actual justo en el momento en el que la energía oscura domina el universo. Sugerente, aunque quizás muy exótico.
En el Tour de Francia, imagina un ciclista que se acerca a un puerto de montaña cuya pendiente crece poco a poco. Para lograr mantener la velocidad de pedaleo constante necesita un desarrollo lo más blando posible que minimice su esfuerzo físico. Para ello cambia a un piñón más grande y usa el plato más pequeño. Gracias a ello, incluso cuando las fuerzas escasean, el ciclista siempre avanza. Aunque parezca que está congelado en la carretera. La misma idea aparece en la fenomenología del campo escalar propuesta por Verde y sus colegas. La energía oscura y la dinámica de los neutrinos se congelan aunque su evolución no se detiene ni marcha hacia atrás.
El artículo es Fergus Simpson, Raul Jimenez, …, Licia Verde, «Dark energy from the motions of neutrinos,» arXiv:1607.02515 [astro-ph.CO]; me he enterado gracias a Ethan Siegel, «Could Dark Energy Be Caused By Frozen Neutrinos?» Starts With A Bang, 13 Jul 2016. Recomiendo en este blog «La energía oscura, la constante cosmológica y la masa de los neutrinos,» LCMF, 10 Ago 2015.
Por cierto, la idea de que la masa de los neutrinos es variable y está acoplada al campo escalar responsable de la energía oscura no es nueva. Ya fue propuesta en el año 2000 por P. Q. Hung, «Sterile Neutrino and Accelerating Universe,» arXiv:hep-ph/0010126. El problema de este tipo de modelos es que suelen ser inestables y requieren ajustes finos del potencial del campo escalar para evitar dicha inestabilidad. Un buen resumen de la situación en Ole Eggers Bjælde, Anthony W Brookfield, …, Domenico Tocchini-Valentini, «Neutrino dark energy—revisiting the stability issue,» J. Cosmol. Astropart. Phys. JCAP 0801: 026 (2008), doi: 10.1088/1475-7516/2008/01/026, arXiv:0705.2018 [astro-ph].
La idea del majorón también es antigua y se remonta al menos hasta Y. Chikashige, R. N. Mohapatra, R. D. Peccei, «Spontaneously Broken Lepton Number and Cosmological Constraints on the Neutrino Mass Spectrum,» Phys. Rev. Lett. 45: 1926 (1980), doi: 10.1103/PhysRevLett.45.1926; el nuevo artículo de Verde y sus colegas combina muchas ideas que llevan mucho tiempo propuestas.
[PS 19 Jul 2016] Este modelo podría ser solución de la reciente tensión entre las medidas de la expansión cósmica observada en Adam G. Riess, Lucas M. Macri, …, Ryan J. Foley, «A 2.4% Determination of the Local Value of the Hubble Constant,» arXiv:1604.01424 [astro-ph.CO]. El propio Reiss propone una idea similar (ver por ejemplo Joshua Sokol, «Ghostly neutrino could be behind cosmic expansion mystery,» NewScientist, 08 Jun 2016).
Esta figura ilustra la evolución con la expansión del universo de la densidad de energía de sus cuatro grandes componentes (normalizadas para que la densidad actual sea la unidad): la energía oscura (DE), la materia oscura (CDM), los fotones (γ) y los neutrinos (ν). La dominancia de la energía oscura sobre la materia oscura es muy reciente a escala cósmica. Más aún, la energía oscura empieza a ser relevante cuando dejan de serlo los neutrinos. Todo ello apunta a un modelo dinámico para la energía oscura basado en un hipotético campo escalar (idea de principios de los 1980) acoplado de alguna forma con los neutrinos.
¿Cuál es el origen del nuevo campo escalar? En el modelo estándar de la física de partículas la única simetría global libre de anomalías es la diferencia entre el número bariónico B y el número leptónico L. El nuevo artículo propone que esta simetría B−L es continua y se rompe de forma espontánea dando lugar a un bosón de Goldstone sin masa llamado majorón. Este bosón es el responsable de dar masa a los neutrinos en forma análoga como le da masa a los electrones el campo de Higgs.
¿Cómo se resuelve el problema de la coincidencia? En las primeras etapas de la expansión del universo, cuando la energía oscura es despreciable, los neutrinos tienen un masa despreciable y se comportan como partículas ultrarrelativistas. Nada cambia en el modelo cosmológico de consenso. Pero el campo escalar crece sin pausa, como el ciclista que sube la montaña, y la masa de los neutrinos crece. Como resultado su contribución al contenido del universo se reduce mientras que la contribución de la energía oscura crece. Esta última empieza a dominar ambas curvas se cruzan y el valor de la densidad de la energía oscura coincide aproximadamente con la masa de los neutrinos en dicho momento.
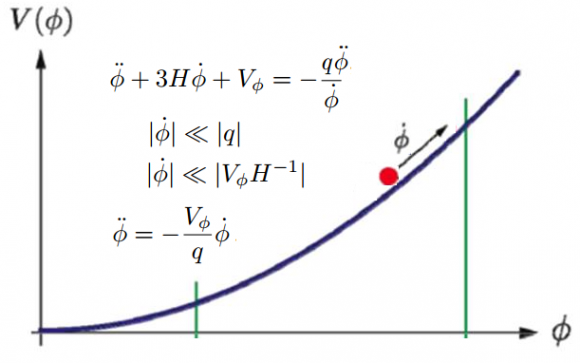
Los modelos en los que la masa de los neutrinos es dinámica y varía con el tiempo suelen ser inestables. Para evitarlo hay que introducir ajustes finos en el potencial de la ecuación de Klein-Gordon del campo. El nuevo modelo de Verde y sus colegas introduce un término que depende de la derivada del logaritmo de la derivada del campo. Gracias a ello la dinámica se vuelve casi independiente de los parámetros del potencial usado. Así se evita el ajuste fino potencial del campo y se resuelve el problema de la coincidencia.
¿Qué predicciones observables realiza el nuevo modelo? Para que funcione los neutrinos tienen que ser fermiones de Majorana con una masa de unos 60 meV. En dicho caso se observará la desintegración doble beta sin neutrinos que nunca se ha observado y busca el experimento español NEXT en el Laboratorio Subterráneo de Canfranc (LSC). Este experimento y otros en curso determinarán la masa de los neutrinos si es superior a 20 meV. En caso contrario el modelo se podrá descartar. Aunque se podría salvar si los neutrinos fueran partículas de Dirac con menor masa y existieran neutrinos diestros estériles con una masa de cientos de MeV.
Los neutrinos generados por la supernova SN1987A que fueron observados en la Tierra permiten restringir el acoplamiento entre el majorón y el neutrino electrónico. Se obtiene una cota superior de 4 × 10−7 para neutrinos de Majorana y de 0,01 para neutrinos de Dirac. Este acoplo también puede ser estudiado de forma experimental. Finalmente, la ecuación de estado de la energía oscura sea w≠1 (en lugar del valor w=1 que predice una constante cosmológica). Esto se podrá estudiar usando medidas de precisión del fondo cósmico de microondas.
En resumen, el modelo combina varias ideas que ya habían sido propuestas logrando la solución a algunas de ellas. Su mayor problema es que es un modelo clásico y su versión cuántica podría estar sujeta a ciertas anomalías que podrían introducir problemas. Futuros estudios tendrán que aclarar si este modelo es realmente prometedor o presenta problemas internas que sus propios autores no son capaces de ver.




Buenas Francis,
Buenas Francis,
No veo como este modelo puede resolver el problema de la constante cosmológica:
https://en.wikipedia.org/wiki/Cosmological_constant_problem
¿Realmente tiene potencial para hacerlo cundo se consiga ‘cuantizar’ utilizando la QFT?
Saludos.
El modelo pretende resolver el problema de la energía oscura, no el problema de la constante cosmológica. Por ello asume que Λ es exactamente cero.
Genial artículo. Lo deja todo muy bien explicado. Realmente, los neutrinos son los superhéroes de las partículas. Por cierto, he encontrado un vídeo que explica muy bien las oscilaciones de neutrinos: https://gabrielrosselloblog.wordpress.com/2017/02/24/que-son-los-neutrinos/
Por si es de interés.
Saludos,
Grabiel, un vídeo de Crespo (Quantum Fracture), @QuantumFracture. Su canal de youtube siempre es una buena recomendación. Crespo ha sido responsable de los vídeos youtube del IFT UAM/CSIC durante el año pasado. Otro canal muy recomendable.