En 2009 el físico Petr Hořava introdujo una gravedad cuántica no relativista (que no es invariante Lorentz). En el caso proyectable es una teoría renormalizable en 3+1 dimensiones; de hecho, la primera teoría cuántica de la gravedad que lo es (los teorías con derivadas altas lo son, pero violan la unitariedad*). El joven físico español Mario Herrero-Valea y varios colegas publica hoy en ArXiv que dicha teoría, además, es asintóticamente libre en 2+1 dimensiones (las teorías con derivadas altas también lo son). Por tanto, el acoplamiento entre los gravitones disminuye a cortas distancias o a grandes energías, por lo que los gravitones se comportan como si fueran partículas libres (lo mismo pasa con quarks y gluones en la QCD en 3+1). Un gran avance hacia una demostración en 3+1 dimensiones, que además muestra que el futuro de la gravedad cuántica de Hořava–Lifshitz es muy prometedor.
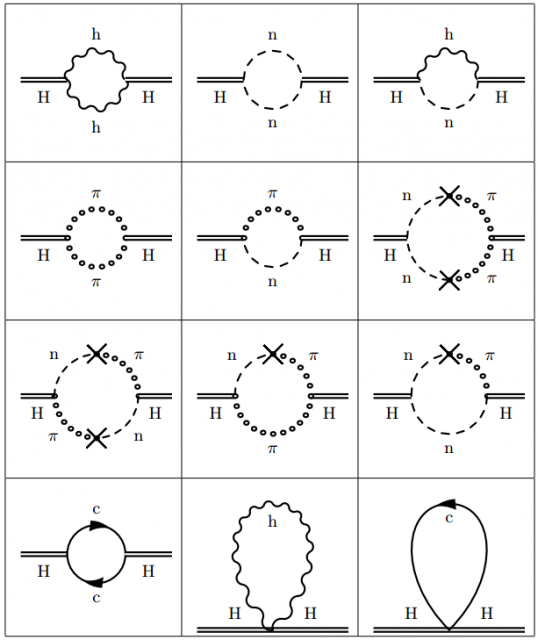
En la gravedad de Hořava–Lifshitz se parte de una foliación del espaciotiempo (se separa el tiempo del espacio) basada en una función N(t,x) llamada lapso. El caso proyectable supone que el lapso solo depende del tiempo, N ≡ N(t). En dicho caso los cálculos cuánticos se simplifican porque se puede asumir que N=1. La teoría presenta tres constantes de acoplamiento, pero solo dos son físicamente independientes, llamadas G y λ. Las funciones beta para ambas constantes (véase la figura) tienen dos puntos fijos, (G,λ) = (0,1/2) y (G,λ) = (0,15/14). Este último es regular y asintóticamente libre.
El artículo es Andrei O. Barvinsky, Diego Blas, …, Christian F. Steinwachs, «Hořava gravity is asymptotically free (in 2+1 dimensions),» Phys. Rev. Lett. 119: 211301 (20 Nov 2017), doi: 10.1103/PhysRevLett.119.211301, arXiv:1706.06809 [hep-th]. Te recomiendo leer también en este blog «La gravedad cuántica no relativista de Horava es renormalizable», LCMF, 09 Dic 2015, y «Nueva moda entre los físicos teóricos: la teoría cuántica renormalizable para la gravedad de Petr Hořava», LCMF, 23 Jun 2009, entre otras. Por cierto, la ř de Hořava se pronuncia como en el caso del músico Dvořák, es decir, algo así como «Horsava» y «Vorsak».
Los detalles del cálculo están más allá de mis conocimientos. Lo más interesante desde el punto de vista divulgativo es que la gravedad de Hořava no proyectable es coherente con todos las observaciones gravitacionales actuales; por ello, no puede ser descartada a día de hoy. Difiera de la teoría general de la relatividad a alta energía, pero eso no es un problema, sino más bien una virtud, ya que en dicho régimen no tenemos observaciones. Aún así, su gran defecto desde el punto de vista puramente teórico es que las bondades de la teoría proyectable no han sido demostradas para la teoría no proyectable. Se requieren futuros avances. Físicos jóvenes, como mi amigo Mario, tienen todavía mucho trabajo por delante para estudiar la versión no proyectable de la teoría.
Hořava en 2009 mostró que su teoría parecía renormalizable contando potencias y conjeturó que podría ser asintóticamente libre. La renormalizabilidad es un hito que ya se ha logrado (aunque en el caso proyectable). Ahora se logra la demostración de que es asintóticamente libre (aunque también en el caso proyectable y solo en 2+1 dimensiones). Sin lugar a dudas, la violación de la simetría de Lorentz, quizás acompañada de una violación de la simetría CPT, parece cada día más razonable a la escalas de energía cercanas a las de Planck.
(*) La teoría de Einstein tiene derivadas de la métrica hasta orden dos y no es renormalizable porque su constante de acoplamiento tiene dimensiones. Hay teorías de la gravitación generalizadas que incluyen términos con derivadas de mayor orden que son renormalizables. Pero tienen varios problemas, siendo el más importante que presentan dos tipos de partículas. Además de los gravitones (partículas de espín dos sin masa), aparecen partículas masivas de tipo gravitón, pero con una energía cinética negativa, llamadas «fantasmas» (ghosts). La existencia de estos ghosts hace que la teoría no sea unitaria, es decir, que en ciertas interacciones las probabilidades sean mayores de la unidad o negativas. No se conoce un mecanismo o simetría que elimine estos ghosts, por lo que se considera que estas teorías con derivadas de mayor orden, aunque sean renormalizables (algo que se sabe desde los 1970), no son una solución adecuada al problema de la gravitación cuántica.



“Petr Hořava introdujo una gravedad cuántica no relativista (que no es invariante Lorentz)”
¿No “mata” eso de entrada cualquier teoría? Por lo que sé, la invariancia Lorentz no ha sido puesta en duda por ningún experimento en los últimos 100 años.
Gracias y saludos.
Albert, si la escala de energía donde aparece la rotura de la simetría Lorentz es suficientemente alta (cercana a la escala de Planck) no hay ninguna evidencia en contra. La teoría de cuerdas es la única que asume dicha invarianza a todas laa energías; todas las demás alternativas (hay cientos) asumen una rotura de esta simetría (al menos en la escala de Planck).
La invarianza de Lorentz es fundamental, violarla lleva a severas inconsistencias, móbiles perpetuos http://motls.blogspot.mx/2008/04/lorentz-violation-makes-perpetuum.html , teóricamente no puedes garantizar invarianza CPT, luego es muy probable que la teoría tenga procesos que la violen, el ser no unitaria implica pérdida de información y rompe los principios más fundamentales de la mecánica cuántica. Es decir no es consistente ni como teoría relativista, ni como teoría cuántica.
Tal vez diga una barbaridad, pero me pone a pensar la propiedad «ser asintóticamente libre» para una teoría cuántica de gravedad. El verdadero problema de la gravedad cuántica (como Francis a divulgado en otras ocasiones) no es cuantizar la teoría, tampoco es describir gravitones «de baja energía», SUGRA resuleve este problema incluso a tres loops (además esta el interesantísmo caso de N=8, D=4), el problema es describir la dinámica de los gravitones «en acoplo fuerte» o sus colisiones a alta energía, encontrar una teoría asintónticamente libre remueve la posibilidad de tratar con agujeros negros o el big bang ¿Qué es una teoría de gravedad cuántica sin agujeros negros?
Sin embargo es muy interesante de cualquier manera, puede ser leído en forma negativa como evidencia de que incluso una «teoría cuántica de gravedad» que no tiene materia , que no tiene otras interacciones, sin posibilidad de agujeros negros y trivial en cuanto a su dinámica de grupo de renormalización no puede ser consistente.
Tal vez «la teoría correcta» necesita por consistencia satisfacer restricciones que la naturaleza resuelve incluyendo los campos y la dinámica específica que observamos. Un poco a la manera de Sugra, la gravedad es parte de un multiplete que contiene materia (gravitinos) y luego es parte inseparable del sector materia.
Ramiro, podemos imaginar un mecanismo parecido al confinamiento en QCD para las singularidades; a cierta distancia el acoplamiento crece fuertemente, aparentando una singularidad a menor distancia, donde en realidad solo hay un conjunto de gravitones libres. Si la escala de energía asociada a la libertad asintótica es alta no se vería afectada la fenomenología clásica «a baja energía» (agujeros negros, modelos cosmológicos, …).
Muy interesante comentario Francis 🙂
Tiene usted razón, el límite IR reproduce la gravedad de Einstein, luego deben ser admisibles soluciones con singularidades. Es astuto recurrir a un mecanismo como el confinamiento de QCD para lograr estados ligados clásicamente singulares 🙂
Si dicho mecanismo no ha sido propuesto sería trabajo muy interesante para investigar.
Gracias por el comentario
La interacción gravitón-gravitón la ha trabajado Alexandre Deur y como resultado obtuvo que esta interacción podría producir los efectos equivalentes a una materia oscura.
Francis ya lo comentó en su momento en este blog y es un trabajo al que yo creo que se le ha prestado poca atención.
Curioseando:
Es verdad que de esto se ha hablado en el blog de Francis https://francis.naukas.com/2012/07/30/los-agujeros-negros-como-condensados-de-bose-einstein-de-gravitones/
Y se habla en la interesante línea en la que Francis respondió mi comentario: Con una analogía QCD y gravedad.
Hay muchos paralelismos muy intrigantes entre teorías de gravedad y cromodinámica cuántica. Por ejemplo está ADS/CFT, también tenemos lo de (Yang-Mills)^2=Gravedad, La dualidad cinemática-color, Los modelos duales que intentaron alguna vez describir la física de los hadrones, la construcción de Sugawara y las álgebras de corriente que intentaron lo mismo.
En el ámbito de la teoría de cuerdas podeís pensar a la cuerda abierta como un meson y la cuerda cerrada como una gluebola. Aquí recordamos que los modos tipo Yang -Mills están la cuerda abierta y los modos graviton en la cerrada. Con el advenimiento de las teorías de alto espín hay especulación sobre cuerdas abiertas (mesones) como estados ligados de «preones de alto espín» (quarks).
La física del plasma de quarks y gluones (ignorando de forma brutal el fascinante diagrama de fases de este régimen) es el sector trans-Hagedorn donde QCD «se libera».
¿Cómo es la física trans-Hagedorn? en teoría de cuerdas. ¿Qué pasa cuando las cuerdas se deconfinan y aparecen los preones de alto espín?, estas son preguntas muy importantes… incluso en el contexto de M theory (porque el volumen de mundo de un stack de M5 branas se entiende como el régimen de deconfinamiento de las little string theories)
Es fascinante el paralelismo entre las dos teorías.