Hasta ahora, la gran sorpresa científica del año 2018 ha sido que el grafeno bicapa con ángulo mágico es superconductor [LCMF, 05 Mar 2018]. La superconductividad emerge de un estado aislante de tipo Mott, al que se retorna tras la aplicación de un campo magnético. Físicos del MIT han propuesto un modelo de Hubbard local con dos orbitales para explicar las correlaciones electrónicas que originan del estado Mott en la estructura de moiré del grafeno bicapa. Chema Pizarro, María José Calderón y Leni Bascones, del Instituto de Ciencia de Materiales de Madrid (CSIC), han estudiado si dicho modelo es compatible con las observaciones experimentales del grupo de Jarillo-Herrero (MIT). Sus resultados indican que las correlaciones electrónicas locales son insuficientes. Por tanto, habrá que considerar el efecto de las correlaciones no locales. Un resultado que me parece muy relevante hacia el secreto de la superconductividad en el grafeno bicapa.
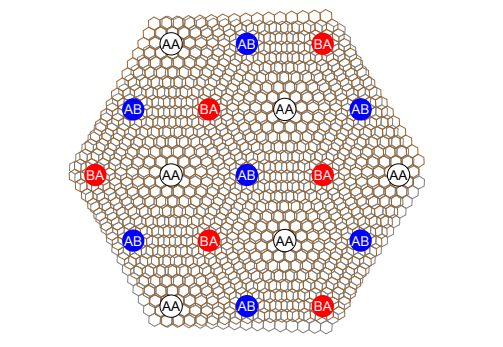
El modelo de Hubbard (1963) describe las cuasipartículas de tipo electrón y hueco en un sólido para explicar su conductividad. Estas cuasipartículas pueden saltar (por efecto túnel) de un sitio a otro de la red (centro del patrón de moiré en el caso del grafeno bicapa) y cuando saltan a un sitio ya ocupado aparece una interacción descrita por cierto potencial efectivo. El modelo de Hubbard permite describir las transiciones de fase entre aislante, conductor y superconductor, incluyendo el estado aislante de Mott. [PS 26 May 2018] El patrón de moiré en la superred tiene simetría triangular con la densidad electrónica centrada en las zonas AA; pero esta simetría no preserva los conos de Dirac. La solución es considerar una simetría de panel de abeja (honeycomb), con orbitales centrados en las zonas AB y BA; pero como la densidad electrónica está en la zona AA, los orbitales efectivos aparentan tener tres lóbulos que se dirigen a cada zona AA. Esta solución sugiere el uso de un modelo de Hubbard con dos orbitales; este modelo está también justificado porque la estructura de bandas del grafeno presenta dos valles (mínimos/máximos en la estructura de banda) situados en los conos de Dirac, que en la superred de moiré se solapan. [/PS]
[PS 26 May 2018] Todo modelo de Hubbard describe interacciones locales, pero permite que las correlaciones electrónicas sean tanto locales como no locales, según la aproximación con la que se estudie. Pero, como el estudio computacional de estas últimas es muy costoso, lo habitual es solo tener en cuenta las primeras. El nuevo trabajo de Bascones y sus colegas indica que son suficientes y que se han de tener en cuenta las correlaciones no locales para describir cómo desaparece la superconductividad en la bicapa de grafeno. Para el modelo de Hubbard con dos orbitales aún no se han publicado estudios que incorporen las correlaciones no locales; habrá que extender los estudios ya realizados con el modelo de Hubbard con un solo orbital, en el que se ha propuesto que estas correlaciones no locales son relevantes para la superconductividad en cupratos. [/PS]
Sin lugar a dudas, los próximos meses prometen ser apasionantes en el camino hacia el modelo teórico que describa la superconductividad en el grafeno bicapa. El nuevo artículo es J. M. Pizarro, M. J. Calderón, E. Bascones, «The nature of correlations in the insulating states of twisted bilayer graphene,» arXiv:1805.07303 [cond-mat.str-el]; estuve hablando con Leni de este interesante tema cuando nos visitó en Málaga el pasado 27 de abril [LCMF, 26 Abr 2018]. El modelo de Hubbard con dos orbitales para el grafeno bicapa ha sido propuesto en Noah F. Q. Yuan, Liang Fu, «A Model for Metal-Insulator Transition in Graphene Superlattices and Beyond,» arXiv:1803.09699 [cond-mat.str-el], y en Hoi Chun Po, Liujun Zou, …, T. Senthil, «Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene,» arXiv:1803.09742 [cond-mat.str-el]; y modelos similares por Long Zhang, «Low-energy Moiré Band Formed by Dirac Zero Modes in Twisted Bilayer Graphene,» arXiv:1804.09047 [cond-mat.mes-hall]; y Jian Kang, Oskar Vafek, «Symmetry, maximally localized Wannier states, and low energy model for the twisted bilayer graphene narrow bands,» arXiv:1805.04918 [cond-mat.str-el].
[PS 26 May 2018] Leni Bascones ha sido tan amable de enviarme una serie de comentarios sobre esta entrada por correo electrónico. En ellos se incluyen correcciones a ciertos errores y aclaraciones a ciertos puntos que no estaban del todo claros. He incorporado dichas correcciones con mi propia redacción. Muchas gracias, Leni. [/PS]
La estructura de bandas del grafeno muestra dos conos de Dirac y cuatro estados asociados, en concreto, dos cuasipartículas tipo fermión (electrón) sin masa efectiva y de quiralidad opuesta, y dos tipo antifermión (hueco) sin masa efectiva. El grafeno bicapa con ángulo mágico (θ ~ 1,1º) muestra un patrón de moiré y una estructura de bandas plana resultado de la degeneración de los conos de Dirac de cada monocapa de grafeno; la carga electrónica se concentra en las regiones centrales (AA) del patrón de moiré, que forman una red triangular análoga a la del grafeno monocapa, pero de arista mucho más grande; en cada celda unidad de la superred, [PS 26 May 2018] en las bandas más cercanas al punto de neutralidad [/PS], se pueden acomodar hasta cuatro cuasipartículas, con lo que la carga puede variar de −4e hasta +4e. En el estado neutro hay dos electrones (cuasipartículas de tipo electrón) por celda de moiré en lugar de las cuatro que caben, es decir, el coeficiente de rellenado por sitio es x=1/2; por debajo de una temperatura de 4 kelvin aparece el estado aislante de tipo Mott con una carga de de −2e hasta +2e por celda unidad de la superred. La superconductividad emerge de este estado aislante Mott cuando la temperatura decrece por debajo de Tc = 1.7 kelvin y el coeficiente de rellenado por sitio es x=1/4.
El modelo de Hubbard con dos orbitales describe el estado de Mott del grafeno bicapa con ángulo mágico sin campos magnéticos externos. Por tanto, parece razonable estudiar la posible transición a un estado superconductor. En este modelo el coeficiente de rellenado en cada celda unidad se define como x = n/(2 N), donde n es el número de cuasipartículas de tipo electrón localizadas en dicha celda y N es el número de orbitales disponibles en dicho sitio. Para el grafeno bicapa se tiene x = 1/4, 1/2, y 3/4. Para x=1/2 tenemos dos electrones por celda, cuatro en la celda de Moiré, con lo que el sistema se comporta como un semimetal en estado neutro. Los estados aislantes de tipo Mott aparecen para x=1/4 y x=3/4, con uno y tres electrones por celda (dos y seis por celda de Moiré); el potencial de interacción del modelo de Hubbard Uc(x) debe cumplir Uc(1/4) < Uc(1/2), luego el sistema es un aislante para x=1/4 y un metal para x=1/2. El estado aislante se vuelve metálico conforme se incrementa la temperatura o se aplican campos magnéticos intensos.
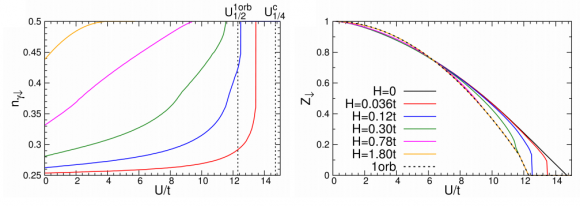
Bascones y sus colegas estudian el modelo de Hubbard con dos orbitales usando la técnica de espín esclavo (slave spin), muy usada en el estudio de los superconductores de hierro (la especialidad de su grupo de investigación). Esta técnica conduce a resultados similares a la teoría dinámica del campo medio (DMFT, por Dynamical Mean Field Theory), y facilita el estudio de los estados para x < 1/2. Los resultados experimentales indican que para x=1/4 el estado aislante de Mott desaparece para campos magnéticos H ∼ 3−6 teslas (es decir, el sistema se vuelve más metálico bajo un intenso campo magnético). Los resultados de la técnica del espín esclavo contradicen este resultado; el estado metálico no se recupera cuando se aplican campos magnéticos intensos. El origen de esta discrepancia se encuentra la hipótesis de localidad. De hecho, Bascones y sus colegas sugieren en su artículo que la no localidad es necesaria para explicar la superconductividad en el grafeno bicapa.
En resumen, el camino hacia el modelo teórico que describa la superconductividad en el grafeno bicapa con ángulo mágico promete ser apasionante. Por ahora, todo indica que habrá que usar un modelo con correlaciones eletrónicas no locales. El desarrollo de modelos que incorporen estos efectos no locales podría ser el camino que nos lleve a desvelar el misterio de la superconductividad de alta temperatura en cupratos. Bascones y sus colegas nos ofrecen una pista, que Uc(1/4) < Uc(1/2), aunque aún no se sabe si esta desigualdad será preservada por las correlaciones no locales. Como siempre, habrá que estar al tanto de hacia dónde nos conduce esta sugerente pista.



Joe, como mola salir en tu blog tras años de leerte desde el anonimato. ¡Qué honor!
Chema, un placer.
Gracias Francis por mantenernos al día. Un honor también saludar a J.M. Pizarro.
¿Qué recorrido se puede prever a esta línea de investigación al hablar de altas temperaturas? Es decir, la máxima a la que se supone que podrían funcionar este tipo de superconductores. Saludos!
Yavi, no sé qué opinará Chema, pero el objetivo es entender el origen; no creo que se pueda incrementar mucho la temperatura crítica (para el grafeno bicapa es 1,7 kelvin, que está muy alejada del récord en cupratos que es 134 kelvin). Una vez entendamos el origen podremos soñar con diseñar nuevos materiales con una temperatura crítica superior a 134 kelvin.
Hola Yavi! Pues creo que lo primero es entender si el grafeno bicapa es un superconductor convencional (en los que el «pegamento» de los pares de Cooper lo dan los fonones de la red) o no convencional. Vamos, cada día sale un nuevo trabajo sobre ello en arXiv.
Después de clarificar esto, no sé hasta que punto son de «fiables» las teorías que hay para predecir las Tc, si resulta que es un superconductor no convencional. Aprovecho y contesto a Francis aquí también: en 2015 se descubrió un superconductor (¡convencional! Nada de cupratos ni superconductores de hierro) que tiene una ¡¡Tc=203K!!; la trampa es que hay que aplicar un montón de presión (creo recordar que son unos 200 y pico GPa). Os cuento un poco para que busquéis más info en la red por si estáis interesados o interesadas: el compuesto padre es H2S y al aplicarle presión se transforma en H3S. Creo que los materiales que tienen H y se comportan de forma convencional tienden a dar altas Tc cuando aplicas presión (como el soñado H metálico…).
Bueno, lo que más mola de este sistema es que abre un montón de posibilidades para estudiar el diagrama de fases en los que hay estás cosas tan curiosas como aislantes de Mott o superconductividad. Cómo son heteroestructuras de materiales 2D es superfácil ir variando el dopaje para encontrar estas fases; de normal, en los demás superconductores primero tienes que crecer el cristal del material y doparlo (os dejo la reflexión de que muchos de ellos son tóxicos y nada limpios…), lo que no siempre es perfecto y mete un «desorden» que puede cambiar las propiedades, te salen materiales «policristalinos», es decir, hay varias orientaciones dentro del cristal, lo que dificulta mucho las medidas y el interpretarlas, etc. Para el grafeno bicapa, basta con exfoliar y hacer 2 capas de grafeno -> pegarlas a un sustrato -> rotarlas mecánicamente -> pegarlas entre sí (lo que es fácil porque entran en juego fuerzas de Van der Waals) -> ponerles un par de terminales -> y aplicar un voltaje, y hala! ya has dopado tu sistema simplemente dandole la vueltecita a la ruedecita de tu aplicador de tensión.
«Superconductividad a 203 K (-70 °C) bajo presiones muy altas» LCMF, 02 Jul 2015
Muchas gracias a ambos por las respuestas :))