
En 1974 el físico teórico Kip Thorne (Premio Nobel en 2017) calculó que un agujero negro en rotación con un disco de acreción puede alcanzar como mucho el 99.8% de su velocidad máxima. Se acaba de publicar en The Astrophysical Journal que el agujero negro en el sistema binario 4U 1630–47 alcanza una velocidad de rotación del (92 ± 4)% del valor máximo. Este número se estima al ajustar con un modelo teórico las observaciones de rayos X realizadas durante el brote de 2016 gracias a los telescopios espaciales AstroSat, Chandra y MAXI. Hasta donde me consta se trata del agujero negro de tipo Kerr cuyo momento angular es mayor entre todos los observados hasta ahora.
Por cierto, el agujero negro Gargantúa que se puede disfrutar en la película Interstellar (2014) de Christopher Nolan rota con un momento angular del 60% del valor máximo. Las imágenes calculadas por el software DNGR (Double Negative Gravitational Renderer) para un valor del 99.9% no gustaron al director. Sin embargo, para que en la superficie del planeta Miller una hora corresponda a siete años lejos de Gargantúa se requiere un valor del 99.999 999 999 999% del valor máximo. Kip Thorne aceptó a regañadientes que en el guión de la película la dilatación temporal fuera tan extrema, a pesar de que se requería superar el límite que él mismo obtuvo en 1974, pues era la única manera de que el padre y la hija se reunieran cuando ella ya era muy anciana.
El nuevo artículo es Mayukh Pahari, Sudip Bhattacharyya, …, Norbert S. Schulz, «AstroSat and Chandra View of the High Soft State of 4U 1630–47 (4U 1630–472): Evidence of the Disk Wind and a Rapidly Spinning Black Hole,» The Astrophysical Journal 867: 86 (02 Nov 2018), doi: 10.3847/1538-4357/aae53b, arXiv:1810.01275 [astro-ph.HE].

La velocidad de rotación de un agujero negro se mide con el llamado parámetro de espín a = c J/(G M²), donde J es el momento angular, M es la masa, G es la constante de gravitación universal y c es la velocidad de la luz en el vacío; nota que a es adimensional ya que [m/s][kg m²/s]/([m³/(kg s²)] [kg²]. Este parámetro se encuentra entre 0 ≤ a ≤ 1, siendo un agujero negro extremal el que alcanza a = 1. Los agujeros negros en rotación se observan en sistemas binarios gracias a la emisión de rayos X de su disco de acreción (materia que roban de la estrella compañera). El brote de 2006 de la binaria de rayos X llamada 4U 1630-47 se observó para energías por debajo de 10 keV (soft X-rays), resultando una señal nula para energías entre 15 y 50 keV (hard X-rays). La ausencia de detección del brote en rayos X duros es clave para la estimación de la alta velocidad de rotación observada.
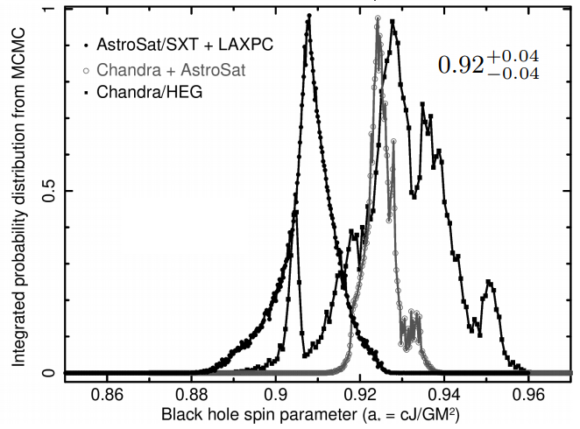
Se han usado modelos de Montecarlo para la simulación de la emisión del disco de acreción y la estimación de la velocidad de rotación del agujero negro. No se conoce su masa (pues aún no se ha observado su estrella compañera), pero se estima a partir de las emisiones en rayos X de su disco de acreción que ronda 10 ± 0.1 masas solares. Por supuesto, el resultado para el parámetro a depende de los datos observacionales que se ajusten (esta figura muestra las tres distribuciones de probabilidad obtenidas); el valor de consenso es a = 0.92 ± 0.04 a tres sigmas (99.7% de intervalo confianza). En cualquier caso, parece claro que el valor es superior al 88%, lo implica que la nueva observación constituye el récord actual.


«Por cierto, el agujero negro Gargantúa que se puede disfrutar en la película Interstellar (2014) de Christopher Nolan rota con un momento angular del 60% del valor máximo. Las imágenes calculadas por el software DNGR (Double Negative Gravitational Renderer) para un valor del 99.9% no gustaron al director. Sin embargo, para que en la superficie del planeta Miller una hora corresponda a siete años lejos de Gargantúa se requiere un valor del 99.999 999 999 999% del valor máximo»
Si para que ambos se reencuentren siendo ella anciana, el valor tenía que ser de 99.99…%, ¿a qué te refieres cuando dices que rota con con un 60% del valor máximo? lo entiendo como una contradicción.
A parte de la dilatación temporal, qué otras consecuencias tiene este valor? me imagino que la fuerza de la gravedad, es así?
Javier, el agujero negro que se ve en la película es diferente del agujero que tendría que verse (para explicar el guión), pero manda el director y guionista (Nolan), no el productor ejecutivo y asesor científico (Thorne).
Gracias por el interesante post.
1) Me parece que hay una errata en el parámetro de Kerr en el cuarto párrafo, debería ser a =(cJ/G(M^2)) en lugar de a = JM/c.
2) Una observación nerd que me recordó la palabra «extremal» es que un agujero negro extremal de Kerr es «holográficamente» equivalente a una CFT quiral con carga central c dada por c = 12J (en unidades de Planck). Se puede leer en el abstract de este artículo clásico: https://arxiv.org/abs/0809.4266 ; evidentemente este resultado vale para un agujero negro con a=1 sobre un fondo AdS vacío (y de cinco dimensiones), pero puede ser divertido ver el orden de magnitud de la carga central que arroja el cálculo.
Asumiendo que el sistema 4U 1630–47 tiene diez masas solares y a = .92 para el mismo se puede obtener que J = 2.88×10^77 (en unidades de Planck) y que la carga central sería c = 3.78×10^78.
Sólo una curiosidad sin moraleja.
Gracias, Ramiro, tienes toda la razón, lo cambio.
Cómo debió ser el guión de esa pelicula, con un agujero negro a un 60% de su velocidad.
Bryan, el planeta Miller no podría haber estando tan cerca, luego cambiaría completamente toda su geofísica; además, la dilatación del tiempo en dicho planeta hubiera sido mucho menor, una hora en su superficie habría sido como una hora y pico en la Tierra, con lo que Cooper nunca hubiera conocido a su hija anciana; etc. Habría que haber cambiado el guión completamente.
Hola. Perdón por plantear aquí una cuestión tan elemental (la verdad es que me da un poco de vergüenza preguntarlo). No entiendo por qué nada puede escapar de un agujero negro. Se dice que es porque hay que alcanzar una velocidad superior a la de la luz para hacerlo y nada en el universo puede alcanzarla. Pero, ¿no se puede abandonar un cuerpo a cualquier velocidad? Cuando se habla de velocidad de escape, yo siempre he entendido que basta con alcanzar esa velocidad para poder escapar de la influencia gravitatoria del cuerpo y ya no hay que aplicar más fuerza, pero que eso no significa que no se pueda abandonar a una velocidad menor, aplicando, por ejemplo, una fuerza constante durante un gran intervalo de tiempo. Se podría imaginar, tal vez, una escalera de enorme longitud y de un material fantástico que fuera desde el suelo hasta un montón de miles de kilómetros más allá de la Tierra. En teoría, cualquier persona equipada con oxígeno, víveres y tal, podría subirla poquito a poquito, aplicando fuerza al subir cada peldaño (que sería un poquito menor cada vez, ya que la intensidad del campo gravitatorio disminuiría al aumentar la distancia a la superficie).
A lo mejor lo que se quiere decir es que, espontáneamente, ningún objeto dejado caer a un agujero negro, puede escapar por sus propios medios. Pero tal vez se podría especular que algún hipotético y exótico fenómeno cuántico en el interior del agujero lanzara una especie de chorro o rayo hacia fuera que pudiera empujar al objeto que cae y alejarlo del agujero. Si la fuerza que ejerciera ese chorro fuera prolongada en el tiempo, podría conseguir que el objeto cruzara hacia afuera el horizonte de sucesos, aunque nunca se superase la velocidad de la luz, ¿no?
Antonio pregunta: ¿no se puede abandonar un cuerpo a cualquier velocidad? No, no se puede. Hay una velocidad máxima que es inalcanzable para un cuerpo con masa que coincide con la velocidad de la luz en el vacío (porque las partículas de luz no tienen masa).
«Algún hipotético y exótico fenómeno cuántico …» La radiación de Hawking es una emisión de radiación por parte del agujero negro que esta caliente a cierta temperatura (demasiado pequeña para ser medida). Pero no es correcto interpretarla como que «algo» escapa del interior del agujero lanzara. Si te interesa el tema en este blog tienes muchas explicaciones de esta hipotética radiación cuántica descubierta por Hawking.
Hola la pregunta de Antonio se me hace muy interesante creo que debes de llamarle velocidad de escape se debería de llamarla velocidad para seguir en rotación y no caer porque es verdad que se puede ir a muy poca velocidad y salir de la atmósfera hasta el espacio igual podría suceder en un agujero negro nada más que las fuerzas de atracción son tan fuertes ahí que desgarraria los átomos y no habría ninguna estructura sólida ni cuerpo que lo soportara
Si según Thorne no se puede superar el 99.8% de su velocidad máxima, ¿qué ocurre con el momento angular de toda la materia que cae al agujero? El momento ha de conservarse ¿no?.
Santaklaus, el momento angular de la materia que entra en el horizonte de sucesos se suma al momento angular del agujero negro. El límite de Thorne para el momento angular máximo del agujero negro con disco de acreción tiene su origen en la radiación emitida por la materia del disco de acreción; a mayor momento angular mayor radiación, lo que implica un curva picado con un límite máximo. Si quieres consultar el sencillo cálculo, lo tienes en K. S. Thorne, «Disk-Accretion onto a Black Hole. II. Evolution of the Hole,» Astrophysical Journal 191: 507-520 (1974), http://adsabs.harvard.edu/full/1974ApJ…191..507T
A propósito de las teorías sobre la gravedad y lo que hay en el interior del horizonte de sucesos de un AN, se me ocurre deducir que: 1- si sólo hay espacio-tiempo vacío y curvado, implica que la masa se ha transformado en energía y por lo tanto sólo queda el efecto de la gravedad (sin masa). Entonces, tendremos que la gravedad es un efecto «holográfico» de otra dimensión, lo que confirmaría una de las hipótesis sobre la naturaleza de esta fuerza. 2- Por el contrario, si dentro del horizonte de sucesos hay un cuerpo compacto (resultante del hecho que al detenerse el tiempo la masa nunca termina de «caer»), tendremos que la gravedad sigue siendo un efecto de la materia. Espero que alguno pueda aportar algo al respecto, pese a que escribo el comentario sobre un artículo que ya tiene varios meses. Desde ya muchas gracias si alguien se toma la molestia.
Ignoramos la teoría definitiva de la gravitación cuántica, así que estas cuestiones siguen sin respuesta. Cualquiera de las posibilidades que propones son posibles pero a día de hoy es imposible discernirlas.
Saludos. Mis felicitaciones al(los) resposable(s) de esta web. Es encomiable que se trabaje para hacer llegar el conocimiento científico al mayor número de personas posibles, en un lenguaje accesible. Muchas gracias.
No soy físico. Mi campo profesional tiene que ver con la Ingeniería de la Telecomunicación, Electrónica, Sistemas de Información e Informática. Pero me apasionan los temas científicos sobre Astronomía, Fisíca y Astrofísica. Sin embargo, de tendencia «muy incrédulo», puedo llegar a ser muy «tozudo» cuando no veo algo claro.
Sobre el tema de los agujeros negros (AN), llevo ya bastante tiempo con una «mosca revoloteando por detrás de mis orejas». Cuando he tenido tiempo he intentado buscar más información en la red, pero sin éxito. Aunque no tiene que ver directamente con la masa, carga y/o velocidad de rotación, MAXIMAS POSIBLES para un AN (como ya tratasteis en otros de vuestros artículos), sí está relacionado con ello.
Y el curioso y «desafiante» comentario de Antonio me ha animado a comentarlo.
Sé que el horizonte de sucesos (HS) de un AN no es una «barrera física», sino un «cálculo matemático» que indica el radio de un AN (¿distancia aproximada hasta la singularidad?) en donde la «VELOCIDAD DE ESCAPE» (VE) sería igual o mayor a la velocidad de la luz (VL). Y se afirma categóricamente que «ningún objeto» que «traspase el HZ» puede volver a salir. Parece que se le pinta como una especie de «barrera espacio-temporal» que «aislaría al objeto» del resto del universo (UNV).
Pero ya hace tiempo que realicé algunos cálculos sencillos que hace que me «incomode» la afirmación anterior. Puede que haya cometído algún error. Lo explico (escribo las formulas linealmente porque no puedo poner los símbolos de fraccion o de exponentes):
Si la fórmula del radio del HZ de un AN sin carga ni «giro»; R = (2 x M x G) : ( C x C ) es correcta;
Y si la fórmula de atracción de dos «astros» en el espacio ; F = (G x M1 x M2) : (d x d) es correcta;
… se deduce que mientras más masivo es un AN, menor es la fuerza de atracción sufrida por un objeto en las inmediaciones del HZ hacia el centro del propio AN.
EJEMPLO 1: AN de 1 Masa Solar (MS) :
Radio de HZ es de unos 3.000 metros (m) ó 3 Kilometros (Km)
La aceleración (ACL) en el HZ sería de unos 15.000.000.000.000 de m por segundo al cuadrado (m p s c)
EJEMPLO 2: AN de 1.000 Masas Solares (MS) :
Radio de HZ es de unos 3.000.000 metros (m) ó 3.000 Kilometros (Km)
La aceleración (ACL) en el HZ sería de unos 15.000.000.000 de m p s c
EJEMPLO 3: AN de 1.000.000 Masas Solares (MS) :
Radio de HZ es de unos 3.000.000 Km
La aceleración (ACL) en el HZ sería de unos 15.000.000 de m p s c
EJEMPLO 4: AN ultramasivo de 1.000.000.000 Masas Solares (MS) :
Radio de HZ es de unos 3.000.000.000 Km
La aceleración (ACL) en el HZ sería de unos 15.000 de m p s c
EJEMPLO 5: AN ultramasivo de 1.000.000.000.000 Masas Solares (MS) :
Radio de HZ es de unos 3.000.000.000.000 Km
La aceleración (ACL) en el HZ sería de unos 15 de m p s c
Así que en un AN de masa solar, si pudiéramos colocar un objeto «inmóvil» en la proximidad del HZ, seía atraído hacia el interior, alcanzando la velocidad de la luz en menos de unos 20 microsegundos.
En este caso, si estrara al AN una persona, las diferencias de fuerzas de atracción gravitatoria entre la cabeza y los pies sería tan grande que le estirarían y lo desgarrarían (efecto espaguetización).
En el ejemplo 3, el objeto sería igualmente atraído y «estirado», pero con una aceleración (menor) de 15.000.000 de m p s c. Y tardaría unos 20 segundos e alcanzar la VL.
Pero en el ejemplo 5 la cosa cambia. Suponemos un AN sin carga, sin «giro», «aislado» sin disco de accrecion. El objeto sufriría una aceleración de «solo» 15 m p s c. Una «gravedad» eqivalente a la de la terrestre mas un 50%. Una astronauta con un buen traje espacial no moriría de momento. No sufriría fuerzas gravitatorias de marea. Y tardaría más de 7 meses en alcanzar la VL.
Obviando los «problemas» para llegar y permanecer allí, en esas condiciones y con esa fuerza de gravedad tan baja, no veo ningún impedimento para que un «satélite» se quedara en órbita al AN a 20 Km, 2 Km, o a 200 m del horizonte de sucesos. O una hipotética estación espacial con astronautas a bordo.
Se podría bajar cualquier «maquinaria» sujeta con un cable grua. O a un astronauta. Y ¿hay alguna razón para que no se le pueda volver a subir?
Y rizando el rizo, si se equipara un «dron espacial» con propulsores con una autonomía de 20 ó 30 minutos para contrarrestar una gravedad de 1 a 2 Gs (iónico, plasma,ramjet, etc), ¿por qué no podría entrar en el HS del AN ultramasivo durante 5 minutos y luego volver a salir?
He leido en algunas web que ya se teoriza que efectivamente un ser humano podría ENTRAR en el HS de un AN supermasivo y NO morir inmediatamente. Pero todas dicen QUE NO SE PODRIA VOLVER A SALIR.
Quizá me he equivocado en los cálculos, o algo se me escapa. Pero en esta caso particular de agujero negro supermasivo, no «veo» ninguna razón para admitir que se pueda entrar en el Horizonte de Sucesos, y sin embargo, categoriar que «NO SE PUEDE SALIR».
Disculpad la extensión de mi comentario. Pero no sabría cómo explicar estas dudas de una forma más concisa. Muchas gracias.
Keo, usas el límite de Roche de la gravitación newtoniana, que no aplica en gravitación relativista; de hecho, no existen órbitas estables, como ocurre en el caso newtoniano. Aún así, hay órbitas metaestables de larga vida, un análogo relativista a las órbitas estables newtonianas; todo agujero negro tiene una curva ISCO (innermost stable circular orbit). Para un agujero negro de Schwarzchild su radio es unas tres veces el radio del agujero negro; si te acercas más, no puedes mantener una órbita metaestable de larga vida.
¿Cómo la nave Endurance en la película Interstellar se acerca más a Gargantúa (que se representa con una rotación del 60 % de la velocidad máxima? Lo cuento en este blog (busca las piezas si te interesa), porque en un agujero negro en rotación (tipo Kerr) la órbita ISCO es más pequeña. Para la película era necesario que Gargantúa rotara al 99.99 999 999 999 99 % de la velocidad máxima; por desgracia, los cálculos físicos sugieren que un agujero negro así no puede ser físico, no puede existir; ninguno puede rotar más allá del 99.8 % de la velocidad máxima. Además, un agujero que rote tan rápido tiene una imagen muy turbulenta, desagradable para el gusto del director de la película. Recuerda que la película es una película y está repleta de especulaciones salvajes.
Saludos Francisco. Muchas gracias por su rapidísima respuesta.
(Lamento que debido a mi situación familiar yo no haya podido responder con anterioridad).
Quizá me expresé mal. Yo en ningún momento estaba comentando los cálculos físicos «super-amañados» de la película , que obviamente tienen su razón de ser por motivos estéticos y artísticos.
Estaba planteando una situación hipotética de un agujero negro «ultra-super-masivo» de 1 Billon de masas solares (billón español, no anglosajón; 1.000.000.000.000). Situado en el centro de una de las burbujas «vacias» que existen en la estructura a gran escala de nuestro universo, sin «nada» alrededor en un radio de 100 ó 200 millones de años luz de distancia. Sin «nada que tragar» , es decir , sin disco de acrecion, sin carga y sin giro (sí «demasiado hipotético»… pero puestos a imaginar… en alguno de los 10 elevado a 500 universos que algunos aseguran que podrían existir, yo podría tener las pintas de un unicornio del color del arcoiris).
Así, que bromas aparte, estaba intentando imaginar o entender cuánta fuerza de gravedad, o qué «cantidad de curvatura», sería suficiente para «separar» a esta «bestia de superagujero negro» del resto de nuestro universo. Con las ecuaciones que encontré en Wikipedia y demás, y para esta «bestia» de 1 billon de masas solares los resultados eran:
Un agujero negro ultramasivo de Schwarzschild «aislado» de 1.000.000.000.000 de Masas Solares:
Radio del Horizonte de Sucesos: unos 3.000.000.000.000 Km ó 0,317 años luz.
La fuerza de gravedad en las inmediaciones del Horizonte serían de unos 15 Newtons por Kg.
Y la aceleración de un objeto «colocado inmóvil» cerca sería de 15 metros por segundo al cuadrado.
A 1.000.000 de Km de distancia del Horizonte la fuerza de gravedad variaría mínimamente.
Lo que no veo, es cómo una fuerza de gravedad tan baja ( y / o ¿curvatura tan pequeña? ), me puede separar en esa zona del Horizonte de Sucesos del resto del Universo. Si puedo entrar 5 minutos sin morir, y llevo algún sistema de «propulsión» que me pueda acelerar a 2 ó 3 Gs durante 15 minutos , ¿por qué no puedo «salir»?.
Debe ser, como tú comentas, que las fórmulas que utilizo no son las correctas , y los resultados son erróneos.
No sé si sería posible que alguno de los participantes en este foro , que conociera las ecuaciones correctas de acuerdo con la Teoría de la Relatividad para este hipotético agujero negro ultramasivo de Schwarzschild «aislado» de 1.000.000.000.000 de masas solares, pudiera realizar los cálculos del radio del Horizonte de Sucesos y la fuerza de gravedad en ese punto , o a 1.000.000 de Km de distancia de dicho horizonte.
O me me pudiera facilitar un link con las ecuaciones correctas.
Muchas gracias.
P.D: Adjunto links con información sobre la posibilidad de entrar con vida en un AN ultramasivo.
========================
En Wikipedia ( https://es.wikipedia.org/wiki/Agujero_negro_supermasivo
Un agujero negro supermasivo tiene algunas propiedades interesantes que lo diferencian de otros de menor masa:
La densidad media de un agujero negro supermasivo puede ser muy baja; de hecho puede ser menor que la densidad del agua, si su masa es suficientemente grande. Esto ocurre porque el radio del agujero negro se incrementa linealmente con la masa, por lo que la densidad decae con el cuadrado de la masa, mientras que el volumen es proporcional al cubo del radio de Schwarzschild…
La cantidad anterior es inferior a la densidad del agua cuando la masa supera ciento treinta y seis millones de veces la masa solar (136.000.000 MS).
Las fuerzas de marea en la vecindad del horizonte de sucesos son sensiblemente menores. Dado que el centro de la singularidad está muy alejado del horizonte, un hipotético astronauta viajando hacia el centro del agujero negro no experimentaría fuerzas de marea significativas hasta adentrarse mucho en el agujero negro.
========================
https://www.infobae.com/america/ciencia-america/2021/02/03/descubrieron-una-forma-segura-en-que-los-seres-humanos-podrian-ingresar-en-un-agujero-negro/
Los agujeros negros son de los objetos más abundantes en el universo, de los más misteriosos y también de los más mortales. Para un humano entrar en uno podría significar un desmembramiento infinito del cuerpo, una muerte lenta, muy lenta.
Pero un dúo de físicos del Grinnell College se dedicó a estudiar la manera en que una persona podría aventurarse al interior de un agujero negro y, aunque no podría contar la experiencia, por lo menos, lograría sobrevivir y descubrir lo que se esconde al otro lado.
Lo primero que explican los profesores Leo Rodríguez y Shanshan Rodríguez es que para que esto sea si quiera posible, el agujero negro tiene que ser supermasivo y estar aislado. Y si la persona ingresa, no podría volver a salir ni comunicarse con nadie del mismo lado del universo.
Keo, la intensidad (aceleración/fuerza) gravitacional en el horizonte de sucesos no es lo que define un agujero negro; como bien indicas para agujeros negros supermasivos es muy inferior a la de la superficie terrestre. Lo que diferencia el horizonte de un lugar lejos del horizonte es la mal llamada «velocidad de escape», que en el horizonte iguala a la velocidad de la luz en el vacío. Así, si cruzas el horizonte, aunque sea una región del espaciotiempo prácticamente plana, no existe ninguna posibilidad de que puedas escapar o comunicarte con el exterior, pues es imposible superar la velocidad de la luz en el vacío. Quizás te resulte difícil de imaginar, pero así es, por definición de agujero negro.