
Toma un conjunto finito de números A (en la figura A = {1, 2, 3, 4}); pon los |A| (=4) números en la primera columna y en la última fila de una tabla; rellena dicha tabla con todas sus sumas y todos sus productos cruzados; cuenta el número de sumas distintas |A+A| (=7) y de productos distintos |A A| (=9). En 1983 los matemáticos Paul Erdős y Endre Szemerédi conjeturaron que |A+A|+|A A| ≳ |A|1+δ, con δ > 0, donde b ≳ a se define como a = O(b logc |A|). Por tanto, si hay un gran número de duplicados en la tabla de sumas, entonces hay pocos en la de productos, y viceversa. El joven matemático George Shakan, Univ. Urbana-Champaign, ha probado que δ = 588/1759 ≈ 0.33, o sea que |A+A|+|A A|≳|A|4/3+5/5277.
Por cierto, el primer progreso desde 1983 lo obtuvo Nathanson en 1997 estimando δ = 1/31; en pocos meses Ford lo mejoró hasta δ = 1/15, y Elekes hasta δ = 1/4. En 2005 Solymosi probó δ = 3/11, que mejoró en 2009 hasta δ = 1/3. Konyagin y Shkredov lo subieron hasta δ = 4/3 + 5/9813, para que Rudnev, Shkredov y Stevens lograran en 2016 alcanzar δ = 4/3 + 1/1509. Por otro lado, hay cotas para otros cuerpos de números, como los enteros modulo un número primo 𝔽p, para los que Shakan y Shkredov obtienen δ = 13/61 ≈ 0.21, o sea que |A+A|+|A A|≳|A|6/5+4/305.
Esta reducción del valor de δ respecto a estimaciones previas se ha publicado en los artículos de George Shakan, «On higher energy decompositions and the sum-product phenomenon,» arXiv:1803.04637 [math.NT], y G. Shakan, I. D. Shkredov, «Breaking the 6/5 threshold for sums and products modulo a prime,» arXiv:1806.07091 [math.CO]. Las tablas que incluyo en esta entrada aparecen en el artículo de Kevin Hartnett, «How a Strange Grid Reveals Hidden Connections Between Simple Numbers,» Quanta Magazine, 06 Feb 2019, cuya lectura te recomiendo.

En la conjetura de la suma-producto no es necesario que los números sean consecutivos, ni que estén en progresión aritmética. Pueden ser números arbitrarios (como las fechas de cumpleaños de un grupo de personas o los números de habitantes de una serie de ciudades).

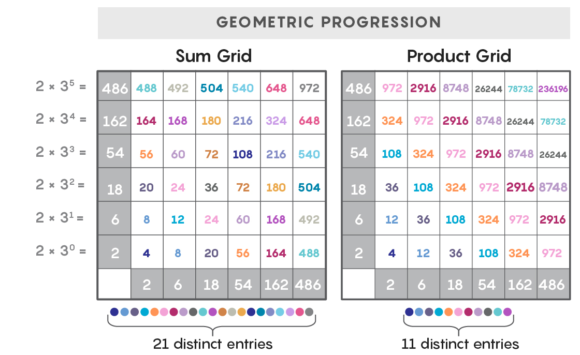
Estas dos tablas que aparecen en el artículo de Quanta Magazine corresponden a progresiones aritméticas y geométricas. Como puedes observar, las progresiones aritméticas conducen a un mayor número de entradas distintas en la tabla de productos que en la de sumas, y en las progresiones geométricas ocurre lo contrario. Cuando los números son aleatorios, puede ocurrir cualquiera de las dos cosas. Se podría esperar que el número fuera próximo a |A|2, sin embargo, Erdős y Szemerédi conjeturaron que una cota mejor sería |A|1+δ, con 0 < δ << 1. ¿Hasta cuánto podrá bajar el valor de δ en los próximos años? Habrá que estar al tanto de los progresos en esta conjetura.


Interesante, y esta conjetura tendrá algo de especial relacionado a los números primos?