Ha vuelto a ser noticia la demostración ontológica del matemático Kurt Gödel (1906–1978) de la existencia de Dios. Se trata de un simple ejercicio de lógica modal que Gödel realizó en 1941 sin mayor interés desde el punto de vista teológico. Su idea era corregir el gran problema de la demostración de San Anselmo. Aunque Gödel era creyente, no era practicante, por lo que nunca habló de la demostración hasta febrero de 1970, cuando pensaba que se acercaba la hora de su muerte. Le enseñó la demostración a su alumno Dana Scott, filósofo y matemático, quien hizo una copia para poderla publicar, pero Gödel no se lo permitió. Tras su muerte, Scott publicó dos versiones de la demostración en 1987 (de hecho, Gödel atesoraba varias). Desde entonces se han publicado muchas otras versiones que refinan los detalles de la demostración. En esta entrada me centraré en la versión de C. Anthony Anderson, “Some emendations of Gödel’s ontological proof,” Faith and Philosophy 7: 291-303, 1990, y su discusión detallada por Christopher Small, “Kurt Gödel’s Ontological Argument,” Part I, Part II & Part III.
 Recomiendo leer la entrada en la wikipedia «Gödel’s ontological proof,» a Trébede, «La prueba matemática de Gödel de la existencia de Dios,» Rescoldos en la trébede, 30 Jun 2011, y la divertida e ingeniosa entrada de Enrique, «Pikachu existe y puedo demostrarlo,» Cuentos Cuánticos, 02 Nov 2013. Prometí mencionar a Pikachu en esta entrada y más abajo lo encontrarás.
Recomiendo leer la entrada en la wikipedia «Gödel’s ontological proof,» a Trébede, «La prueba matemática de Gödel de la existencia de Dios,» Rescoldos en la trébede, 30 Jun 2011, y la divertida e ingeniosa entrada de Enrique, «Pikachu existe y puedo demostrarlo,» Cuentos Cuánticos, 02 Nov 2013. Prometí mencionar a Pikachu en esta entrada y más abajo lo encontrarás.
Ante todo, te aclaro lo que no vas a encontrar en esta entrada: una explicación en detalle la demostración (la figura de abajo es la versión que aparece en la wikipedia). Lo que pretendo es justificar el tipo de demostración siguiendo la línea de la discusión de Christopher Small. Por supuesto, debes tener presente que en todas las demostraciones matemáticas de la existencia de Dios el argumento es similar. Se define un objeto matemático llamado “Dios” que cumple con una propiedad muy sencilla y se introducen una serie de reglas de razonamiento lógico (axiomas) asociados a dicha propiedad. La demostración matemática procede paso a paso hasta asegurar la existencia de este objeto en un universo en el que sean válidas dichas reglas. Nada más y nada menos. No hay ninguna relación entre el objeto matemático “Dios” y lo que tú puedas pensar que es Dios, seas creyente o ateo.
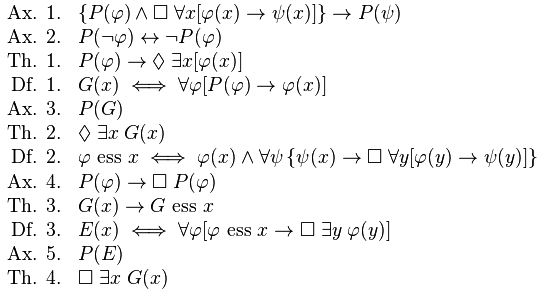 La demostración ontológica de Gödel es una versión moderna del argumento ontológico para la existencia de Dios de San Anselmo de Canterbury (1033–1109), un monje benedictino que fue arzobispo de Canterbury desde 1093 hasta su muerte. Su argumento, de forma resumida, es el siguiente: “Por definición, Dios es aquello de lo cual nada mayor puede concebirse. Por tanto, es imposible concebir que Dios no existe, pues de lo contrario podríamos concebir algo mayor que él, a saber, un Dios que sí exista. Así pues, es inconcebible que Dios no exista; luego existe.»
La demostración ontológica de Gödel es una versión moderna del argumento ontológico para la existencia de Dios de San Anselmo de Canterbury (1033–1109), un monje benedictino que fue arzobispo de Canterbury desde 1093 hasta su muerte. Su argumento, de forma resumida, es el siguiente: “Por definición, Dios es aquello de lo cual nada mayor puede concebirse. Por tanto, es imposible concebir que Dios no existe, pues de lo contrario podríamos concebir algo mayor que él, a saber, un Dios que sí exista. Así pues, es inconcebible que Dios no exista; luego existe.»
Esta demostración utiliza argumentos de lógica modal, aunque la lógica modal no se formalizó de forma rigurosa hasta principios del siglo XX. La razón por la que no se usa la lógica de predicados ya se conocía en la época de Anselmo, se puede demostrar la existencia de Dios de una forma mucho más corta (aunque menos satisfactoria): “Si no es cierto que “Dios existe implica que castigará a los buenos”, entonces Dios existe.” Esta demostración es resultado de la siguiente paradoja de la implicación lógica: Si no es cierto que P implica Q, entonces P. Recuerda que la implicación lógica “P implica Q” significa que si P es falso, “P implica Q” es verdadero, y si P es verdadero, “P implica Q” es verdadero o falso según lo sea Q. La implicación lógica presenta múltiples paradojas, como que si Q es verdadero, entonces “P implica Q” es verdadero para todo P (incluso sin que haya ninguna relación entre P y Q). Estas paradojas resultan extrañas para la intuición, rayando lo absurdo. Para evitar estas paradojas la demostración de Gödel utiliza el sistema S5 de la lógica modal de Lewis y Langford (1932).
El lógico estadounidense Clarence I. Lewis (1883-1964) formalizó en 1918 la lógica modal introduciendo la llamada implicación estricta para evitar las paradojas de la implicación lógica. La lógica modal extiende la lógica de predicados con las nociones modales de “necesidad” (o “es necesario que”), “posibilidad” (o “es posible que”), “imposibilidad” y “contingencia”. Una proposición verdadera es llamada proposición necesaria (por necesariamente verdadera). Una falsa es llamada imposible. Las demás se llaman contingentes. Una proposición posible es la que no es imposible. Son posibles todas las verdaderas y necesarias. Se define P implica estrictamente a Q si y sólo si necesariamente P implica a Q. En esta entrada no puedo discutir en detalle las diferencias entre la lógica de predicados y la lógica modal, ni puedo definir todos los operadores y reglas de inferencia que utiliza. Los interesados encontrarán mucha más información en la wikipedia.
El mayor problema de la lógica modal es la semántica pues no existe una única interpretación (un único universo modelo para dicha lógica). Por ello se suele decir que la semántica de la lógica modal refleja la idea del multiverso (describe todos los universos posibles). Hay varias lógicas modales, pero la más completa y que mejor expresa las intuiciones semánticas de todos los mundos posibles es llamada S5. que incluye el axioma “si es posible que P sea necesario, entonces P es necesario”, que permite razonar que “si P es necesario, es necesario que lo sea”, que “si P es posible, es necesario que lo sea” y que “si P es contingente, es necesario que lo sea”. La gran ventaja de la lógica modal S5 es que se pueden reemplazar todos los operadores modales por cuantificadores cuyo domino son todos los universos posibles.
Demostrar la existencia de Dios en una lógica modal S5 es fácil. Charles Hartshorne ideó en 1962 la siguiente argumentación. Para demostrar que “Dios existe” hay que demostrar que “existe un objeto en un universo que tiene la propiedad de ser máximamente perfecto”. Para ello se argumenta como sigue: Como resulta que “si Dios existe es necesario que exista” y “es posible que Dios exista”, deducimos la conclusión “es necesario que Dios exista.” Omito la formulación en símbolos y la demostración, que son fáciles de encontrar en la web.
Todas las demostraciones que hemos visto hasta ahora se basan en asignar al concepto de “Dios” una propiedad de máximo. La demostración de Gödel, por el contrario, trata de usar un argumento de mínimo, por eso se centra en la “esencia” de las propiedades positivas que caracterizan a Dios. Pero antes de discutirla en más detalle, permíteme una curiosidad para relajar la tensión.
Hay quienes hacen sudokus para pasar el rato y quienes los usan para entrenar su mente. A estos últimos les recomiendo estudiar teoría axiomática de conjuntos. Sólo ellos podrán disfrutar de la demostración de Gödel de la existencia de Dios. Un buen punto de partida es el maravilloso librito de Jesús Monterín, “Teoría axiomática de conjuntos,” Ariel, Barcelona, 1971. He de confesar que, siendo adolescente, estudié este libro gracias al ejemplar que había en la Biblioteca Pública de Fuengirola (supongo que seguirá allí). No lo he vuelto a leer, pero tengo muy buen recuerdo. Rellené libretas enteras repitiendo las demostraciones de mi puño y letra. Hoy en día ya se me ha olvidado todo lo que estudié. Los años no pasan en balde.
 Como ya he comentado el argumento ontológico de Gödel para la existencia de “Dios” es una versión revisada del argumento ontológico de Anselmo. La mejor manera de formalizar un argumento ontológico sobre la existencia de “Dios” es usar la lógica modal. Definir a Dios como creador del universo, como omnipotente o como omnisciente no permite construir una demostración de su existencia utilizando la lógica modal. Por ejemplo, un argumento de tipo “Dios es omnisciente; Dios sabe que existe; luego Dios existe” no se puede formalizar; lo máximo que podríamos demostrar es que “posiblemente Dios existe”, es decir, la existencia de Dios sería una verdad contingente, pero nunca una verdad necesaria.
Como ya he comentado el argumento ontológico de Gödel para la existencia de “Dios” es una versión revisada del argumento ontológico de Anselmo. La mejor manera de formalizar un argumento ontológico sobre la existencia de “Dios” es usar la lógica modal. Definir a Dios como creador del universo, como omnipotente o como omnisciente no permite construir una demostración de su existencia utilizando la lógica modal. Por ejemplo, un argumento de tipo “Dios es omnisciente; Dios sabe que existe; luego Dios existe” no se puede formalizar; lo máximo que podríamos demostrar es que “posiblemente Dios existe”, es decir, la existencia de Dios sería una verdad contingente, pero nunca una verdad necesaria.
La clave para construir una demostración de la existencia necesaria de Dios es definirlo utilizando su esencia. Si definimos que “el Papa es una persona que viste de blanco”, cualquier persona que vista de blanco sería el Papa, lo que es falso. Para definir al Papa tenemos que utilizar una propiedad esencial que le caracterice de forma unívoca; por ejemplo, “el Papa es el obispo de Roma”. Otra propiedad esencial es “llevar puesto el anillo papal.” En general, para definir un objeto sólo debemos usar propiedades esenciales de dicho objeto. En lógica modal una propiedad de un objeto es esencial si es necesario que ese objeto tenga dicha propiedad. Cualquier otra propiedad es contingente y pueden existir otros objetos que tengan dicha propiedad. La esencia de un objeto es una propiedad esencial a partir de la cual se pueden derivar todas las demás propiedades esenciales de dicho individuo. La esencia de ser Papa puede ser “ser el obispo de Roma” que implica la propiedad esencial “llevar puesto el anillo papal” y cualquier otra propiedad esencial.
¿Cuál es la esencia de Dios? Para Anselmo la existencia es una propiedad esencial de Dios, como también lo son que Dios es el creador de todo, que Dios es omnipotente, omnisciente, etc. Dios es aquello por lo que es imposible que exista un ser superior en ningún aspecto. El problema del argumento ontológico de San Anselmo, como criticaron Immnauel Kant y otros filósofos, es que el concepto de «existencia no es una propiedad». Gödel sustituye este concepto por la propiedad de que sea «necesaria su existencia», un cambio sutil para el lego, pero muy importante desde el punto de vista formal, semántico e interpretativo en lógica modal.
Para entender mejor la demostración de Gödel conviene recordar la demostración de San Anselmo escrita en lógica modal. Seguiré aquí la versión del filósofo Charles Hartshorne (1962). El primer axioma de Anselmo es “Axioma 1: Es posible que Dios exista”. Este axioma no distingue entre lo concebible y lo posible. Yo puedo concebir un número entero par mayor que dos que no se puede escribir como la suma de dos números primos. Sin embargo, el hecho de que yo lo conciba como un entero no significa que posiblemente exista. La idea de Anselmo es que es imposible concebir un ser más grande que Dios, por ello propone el “Axioma 2: Si la existencia de Dios es posible, entonces es necesaria”. Para Anselmo Dios tiene como propiedad esencial la máxima perfección. A partir de los dos axiomas anteriores la lógica modal S5 permite demostrar que “Dios existe necesariamente”.
Una parodia del argumento sería la siguiente. Definición: Un Pikachu es un pokémon amarillo que se parece al roedor llamado pika y que existe. Por lo tanto la lógica modal permite demostrar que Pikachu existe. Obviamente, esta demostración no resiste un análisis matemático riguroso. La definición que hemos hecho de un Pikachu no refleja su esencia (aunque quizás en Cuentos Cuánticos no opinen lo mismo).
El mayor problema de la demostración de Anselmo es el primer axioma, ya que la posibilidad de la existencia de Dios no implica la necesidad de la existencia de Dios. Gödel trata de transformar el Axioma 1 en un teorema introduciendo axiomas más fundamentales. Para ello, siguiendo a Gottfried Leibniz, decide dar un rodeo argumental que pasa por describir las propiedades esenciales y la esencia de Dios. Gödel considera que las propiedades esenciales de Dios son propiedades positivas, es decir, son cualidades buenas. Se puede pensar que hay un contenido moral en este concepto. Sin embargo, Gödel no formaliza el contexto moral de estas propiedades, para él una propiedad es positiva en un sentido de pura atribución intrínseca (un concepto metafísico que me llevaría demasiado tiempo discutir aquí). La relación con lo moral o lo estético es una cuestión accidental para Gödel, sin mayor importancia y por tanto no es necesario describirla en la demostración. Quizás el lector opine todo lo contrario (como César @EDocet en este tuit), pero así es la demostración de Gödel.
 Permíteme discutir ahora la demostración de la existencia de Dios de Gödel en su versión de Anderson. Presentaré los axiomas, las definiciones y los teoremas sin demostración (los interesados la pueden estudiar en detalle en la web de Christopher Small). Mi idea es explicar por qué son como son, sin preocuparme por los detalles formales de la demostración. Espero que esto ayude a los lectores interesados en tener una idea de la lógica argumental de la demostración.
Permíteme discutir ahora la demostración de la existencia de Dios de Gödel en su versión de Anderson. Presentaré los axiomas, las definiciones y los teoremas sin demostración (los interesados la pueden estudiar en detalle en la web de Christopher Small). Mi idea es explicar por qué son como son, sin preocuparme por los detalles formales de la demostración. Espero que esto ayude a los lectores interesados en tener una idea de la lógica argumental de la demostración.
Axioma 1: “Una propiedad es positiva si y sólo si su negación es negativa”. Axioma 2: “Una propiedad es positiva si contiene necesariamente una propiedad positiva”. Estos dos axiomas de carácter técnico son necesarios en la lógica modal S5 para demostrar el primer teorema: “Teorema 1: Una propiedad positiva es lógicamente consistente, es decir, existe algún objeto con dicha propiedad y por tanto todo lo positivo es posible”. La consistencia lógica también es llamada ejemplificación, es decir, que si no hay ningún objeto que tenga cierta propiedad, entonces esta propiedad no puede ser positiva. Gödel sigue la línea argumental de Leibniz en que la esencia de Dios es «independiente de la estructura accidental del mundo». Nuestro mundo contiene el bien y el mal, pero el mal de este mundo sólo puede ser accidental y no es necesario. Decir lo contrario contradice el Axioma 2. El Teorema 1 declara que lo bueno (las propiedades positivas) siempre es posible (siempre son posibles), lo que apoya el siguiente principio de Kant (fuerte opositor del argumento ontológico): «Deber ser implica poder ser», es decir, si uno tiene la obligación de hacer algo, entonces debe ser posible hacerlo.
Para definir a Dios como el objeto cuya esencia es la perfección absoluta, primero hay que introducir lo que es la esencia. Definición 1: “Una propiedad es la esencia de un objeto si y sólo si el objeto tiene dicha propiedad y esta propiedad es necesariamente mínima, es decir, todas las propiedades esenciales del objeto se derivan de su esencia.” Nada implica que la esencia sea única, pero la minimalidad sugiere cierta unicidad. La cuestión de si cada individuo tiene una esencia está en el corazón del existencialismo de Jean-Paul Sartre, no entraré en más detalles.
La siguiente etapa del argumento de Gödel es definir el significado de la palabra «Dios”. Definición 2: “Algo es “semejante-a-Dios” si y sólo si posee la esencia de todas las propiedades positivas, es decir, si todas sus propiedades esenciales son positivas y si su esencia es tener todas las propiedades positivas.” Esta definición como tal no implica que haya un único objeto semejante-a-Dios. Además, esta definición tampoco implica que todas las propiedades de Dios sean positivas, sólo sus propiedades esenciales tienen que serlo. Desde el punto de vista matemático lo más importante es que se usa un cuantificador (“todas sus propiedades”) lo que significa que hay que interpretar estas propiedades en todos los mundos posibles. La interpretación de la lógica modal siempre se realiza en el sentido semántico del multiverso (el conjunto de todos los universos posibles).
El tercer concepto que introduce Gödel es la propiedad de existencia necesaria. La crítica de Kant a Anselmo se basa en que la existencia no es una propiedad, luego Gödel define “Definición 3: Decimos que algo existe necesariamente si tiene una propiedad esencial.” Puede parecer obvio que la propiedad ser semejante-a-Dios es positiva, pero es imposible demostrarlo con todo lo anterior. El problema es que no se puede demostrar que tener un conjunto de propiedades positivas sea una propiedad positiva. Luego Gödel introduce el Axioma 3: “Ser semejante-a-Dios es una propiedad positiva.” En este momento Gödel puede demostrar el primer axioma de Anselmo que afirma que posiblemente Dios existe. Corolario 1: “Ser semejante-a-Dios es una propiedad lógicamente consistente, es decir, existe algún objeto con dicha propiedad”. Esto no es una demostración de que Dios existe, pues hay que trabajar más para demostrar que Dios necesariamente existe. Pero el primer gran paso ya ha sido dado.
Si las propiedades positivas de Dios son maximales, tenemos que añadir el siguiente Axioma 4: “La existencia necesaria es una propiedad positiva.” Ahora ya se puede demostrar el siguiente Teorema 2: “Si un objeto es semejante-a-Dios, entonces ser semejante-a-Dios es la esencia de dicho objeto”. Y ya casi se ha acabado la demostración pues para demostrar el teorema final basta seguir el argumento de Anselmo. Teorema 3: “Necesariamente existe un ser semejante-a-Dios.”
¿Se trata de una demostración “correcta” de la existencia de Dios? Obviamente se trata de una demostración matemática correcta en la lógica modal S5, pero cada persona tiene una idea diferente de lo que es Dios. En esta demostración no hay contenido teológico. Quizás algunos filósofos puedan quedar satisfechos, pero en general poca gente lo estará. Incluso si el argumento es correcto en todos sus aspectos, como no se especifica qué es una «atribución pura» para una propiedad positiva, bien se podría haber demostrado que alguna ecuación matemática que rige el universo es lo semejante-a-Dios que necesariamente existe.
¿Se puede sustituir «semejante-a-Dios» por «pikachiano» y obtener una demostración de la existencia de Pikachu? Obviamente, no. Pero si queréis echar unas risas…
PS: Por cierto, en relación a la noticia esta semana sobre el logro de los científicos Christoph Benzmüller, de la Universidad Libre de Berlín, y Bruno Woltzenlogel, de la Universidad Técnica de Viena, me gustaría aclarar que sólo han verificado por ordenador la demostración del matemático Kurt Gödel de la existencia de Dios. El nuevo trabajo de Benzmüller y Woltzenlogel valida la demostración mediante un software de demostración automática de teoremas. Esto no aporta nada nuevo a la demostración, sólo confirma que el software funciona correctamente.
PS (4 Nov 2013): Recomiendo leer a Arturo Quirantes, «Gödel y la demostración de algo llamado Dios,» Naukas, 04 Nov 2013. Confieso que no me gusta el tono ligero de algunos de los razonamientos de mi amigo Arturo, pero se lee fácil y puede ser interesante para muchos lectores de mi entrada.



Existir se define como pasar desde el ” no ser” al “ser” viene de sisto (Estar) y ex(Desde fuera), Por otro lado se sabe por la MC que hay partes de esta definición que quedan obsoletas a pequeña escala, tales como la dualidad o el principio de incertidumbre, por tanto, es una tarea sin fin tratar de demostrar la existencia de algo “en” la realidad, porque su propia definición esta limitada. En ese Caso es mas correcto decir que algo es Real, conceptuando Real en una categoría superior que la realidad, la realidad es perceptible, medible etc. Lo Real es el universo que tratamos de conocer a través de la realidad.
Por lo tanto es mejor evitar tratar con palabras que no corresponden como la palabra Existir y hablar de Real y Realidad solamente.
¿Se puede comparar la sed con la angustia existencial? La primera es real y la segunda existe.
hay cosas que son reales y no existen, por ejemplo la singularidad , eso ocurre porque real y realidad se diferencian, no son lo mismo. la realidad es medible, palpable, inuitiva como la sed.
Magnífico trabajo en el que Francis derrocha todo su ingenio. Felicitaciones:
Alejandro Álvarez
No creo que intentara pasar de axioma a teorema porque son conceptos distintos.
A nadie le importa tus creencias Lol
«aquello de lo cual nada mayor puede concebirse»… eso suena mas bien a intentar demostrar el lema de Zorn, lo cual en Zermelo–Fraenkel equivale al axioma de elección. ¿Podria Godel haber entrado en esto no por argumentos religiosos, sino intentando buscar otros sistemas donde probar el lema de Zorn indepencientemente de AC?
Tú observación es muy buena A Rivero.
Cuando leí la frase con la que abres tu comentario entre comillas pensé exactamente en lo mismo, y de hecho tú pregunta es en facto algo que interesaba a Godel (el mismo creo recordar que mostró la consistencia del esquema Zermelo-Fraenkel+ la negación del axioma de elección).
Entiendo completamente tu intuición y me gusta como lo interpretas, la dificultad creo yo es que «aquello de lo cual nada mayor puede concebirse» en realidad no necesariamente es el elemento maximal que garantiza el lema de zorn, me suena más a que Dios tendría que ser la cota superior de un conjunto parcialmente ordenado de las hipótesis del lema, entonces dudo de la equivalencia.
¿Alguien ha leído algo sobre los intentos de Cris Isham por fundamentar la «lógica» de la escala de planck usando teoría de topos?
Relacionando el tema de Dios con el AC (axioma elección) puede ser interesante echarle un vistazo al paper «God exists» del lógico «relevante» Bob Meyer (que por cierto era cura). http://www.jstor.org/stable/2215186
“Existir se define como pasar desde el ” no ser” al “ser” viene de sisto (Estar) y ex(Desde fuera)”.
Hum…, si algo pasa de no ser a ser, de no existir a existir, ese no ser y no existir tiene movimiento, luego ya era algo antes de pasar a ser y existir. Manifestarse o no manifestarse son cualidades de movimiento, pero no presupone que el ser deje de ser cuando no se manifiesta.
Lo he notado y tiene un extraño parecido al que hay entre una particula y su función de onda, en la doble rendija por ejemplo antes de medirla es función de onda, luego en este caso la función de onda es real y la partícula es la realidad, al interpretarlo como existe o no existe se es demasiado limitante y no hay argumentos suficiente para decir que antes de la medición «existiera» algo como mencionas. Mi opinión al respecto es que antes de la medición no existe nada porque nada puede medirse, pero todos sabemos que hay algo, luego ese algo es «Real» que se manifiesta en la «realidad» al colapsar. Puede parecer juegos de palabras pero la diferencia es que las palabras real y realidad pueden dar solución a la paradoja de la medición pero la palabra existir no, trae puros problemas.
Esto me lleva a pensar que la nada, lo que no es ni existe, no está fuera del ser infinito sino dentro del mismo. Entonces el problema del límite no está fuera sino dentro, esto abre una serie de preguntas físicas, filosóficas y matemáticas interesantes.
Hola, Ramiro. Hay una explicación magnífica del axioma de elección escrita por Shaugan Lavine “Comprendiendo el infinito”, (Fondo de Cultura Económica, 2005). Está en las páginas 119-136.
Citando a Maddy, escribe Lavine que parte de la confusión epistémica que rodea al axioma de elección se debe a una confusión entre conjuntos y propiedades definibles, pero una vez eliminada la confusión el axioma de elección aparece como uno de los axiomas menos problemáticos de la teoría de conjuntos.
Gracias por la recomendación Artemio. Lo voy a leer.
Ramiro, estupendo, es un libro magnífico. Atento al capítulo VII donde Lavine menciona el ataque argumental de Gödel al escepticismo de Poincare, Weyl y Brouwer respecto de la teoría cantoriana de conjuntos 😉
«Si introducimos el siguiente axioma 3…», «si introducimos el siguiente axioma 4…», «si introducimos el siguiente axioma 5…».
Dime lo que quieres que demuestre y lo haré con el suficiente número de axiomas…. Y encima son axiomas a posteriori, cuando los necesitas. Si los introduces cuando lo necesitas, es porque no estas tratando de demostrar si algo es de una forma u otra, estás tratando de ver lo que ya das por supuesto que es así, y nada te detendrá a la hora de introducir todos los axiomas que hagan falta para ello.
david, es al revés, se trata de usar el mínimo de axiomas, no el máximo. El que un matemático se decida por el axioma de elección no es el problema, lo que tiene que hacer es demostrar su consistencia. El axioma de elección surge en el contexto de la teoría cantoriana de conjuntos, contribuye al buen orden de las colecciones combinatorias. Otra cosa diferente es que la comunidad matemática coincida o no, pero la coincidencia y la discrepancia dependen de la consistencia de los argumentos que entran en liza.
La geometría no euclídea falsa con axiomas a la geometría clásica en determinados supuestos, pero un geómetra no puede añadir axiomas a la ligera, tendrá que demostrar la consistencia de sus postulados. No es tan fácil como lo planteas.
Los seres humanos tenemos nociones intrínsecas sobre la geometría, y con los axiomas de Euclides se estableció un sistema que recreaba nuestras nociones (a veces, las cosas no son tan evidentes y por eso se extendió a geometrías no euclídeas, no evidentes desde el principio).
Eso es exactamente lo que hace esta demostración: tiene una noción predefinida de lo que significa Dios, y trata de encontrar el mínimo número de aximoas que lo demuestren. Pero partir sin tener la noción de Dios, y descubrirlo tal como se hace con un teorema, es algo completamente distinto.
Genial como siempre, y gracias por el material que proporcionas.
Darío.
Yo creo que el fallo de ambas demostraciones está en el marco de referencia, grande>>pequeño, que se da por válido como un preaxioma implícito; cuando no está claro en las propiedades que proponen (grandeza San Anselmo o positividad de Göedel). Un número es más grande que otro, principalmente porque el número en sí habla de cantidad, de nada más, por lo que una de sus propiedades intrínsecas, lo que le define, es ser mayor o menor que otro número.
Pero en términos lógicos, un ser no puede ser más perfecto/grande que otro, como mucho lo puede serlo para una categoría, pero no para cualquier categoría imaginable. En el mismo instante que haya algo mejor que Dios en cualquier cosa, Dios dejaría de ser real, pues perdería su razón de ser, la perfección.
Me faltó añadir que muchas de las categorías que hacen Dios Dios son subjetivas, por lo que no pueden ser expresadas matemáticamente y yo puedo tener una idea de bondad diferente a la de otro, por lo que es imposible imaginarse alguien con una bondad perfecta, que satisficiera a todos.
Creo que aqui no se habla del Dios Cristiano en si, sino de un Dios generico digamos, pero vamos, sigue siendo algo tan subjetivo asi como vos decis… Ni hablar que asociar dios a bondad lleva ya una subjetividad implicada. ¿Porque un dios bondadoso es mas creible que uno cruel? ¿Es porque nos cae bien psicologicamente? Hacemos el mismo planteo con cada caracteristica que se le asigna a un dios ¿Porque cruel? ¿Porque indiferente?, y asi…
“Un número es más grande que otro, principalmente porque el número en sí habla de cantidad, de nada más, por lo que una de sus propiedades intrínsecas, lo que le define, es ser mayor o menor que otro número”….
Hum…, los números también son proporciones no sólo cantidad. ¿Es mayor +1 que -1? ¿Es mayor una potencia que una raíz? Si un infinito es mayor que otro, ¿por qué son ambos infinitos?
Tienes razón, no me había parado a pensarlo. Lo que hace mayor a un número que otro es la geometría en el que están definidos, o por decirlo de una manera más prosaica, las reglas matemáticas que los gobiernan, que no tienen porqué ser las habituales.
Es fácil establecer unas reglas matemáticamente consistentes en el que -1 sea mayor que 1.
Cuidado, que yo no quiero tener la razón, no lo digo por tenerla 😉
Pero tal como dices, y sigo a Hegel y Kant en este punto, conviene prestar atención al aspecto relacional de los números, a sus magnitudes extensas y a lo que describen y notan.
david, estamos de acuerdo, pero sólo una nota; tener nociones predifinidas no sólo no es malo sino que es saludable, tú mismo lo escribes: “Los seres humanos tenemos nociones intrínsecas sobre la geometría”, las tenemos porque las necesitamos.
Hay un error extendido en el debate filosófico acerca de los apriorismos, el apriorismo puede surgir de una intuición inesperada y fértil, no todo lo apriorístico es sistemático. Hegel y Kant defendieron las magnitudes extensas, que era un modo de equilibrar el reduccionismo inherente al formalismo matemático.
Explicitado el matiz, coincido contigo.
Nunca entenderé por qué gente aparentemente culta y racional habla de dioses utilizando el singular y las mayúsculas. El pensamiento crítico ayuda bastante a desprenderse de tradiciones y legados localistas, y a dejar de mirarse el ombligo cultural.
Goomer, los cultismos no sólo son culturales sino inerciales, pertenecen a la tradición lingüística. Esto poco tiene que ver con la cultura del escribiente, es un modo de facilitar al lector el hilo de lo que lee. El resto de tu comentario no lo entiendo, no sé quién se mira el ombligo.
«Nunca entenderé por qué», ¿no seria estar predispuesto a no entender?
Adenda. Aunque algunos no lo saben, Hegel y Kant manejaban bien la matemática y la geometría, pero la mirada que posaron sobre ambas es filosófica, lo que añade una perspectiva más amplia que el mero formalismo numérico.
Bajo mi humilde opinión, cualquier forma lógica de buscar a dios llevará unívocamente a encontrar el universo, pues desde el punto de vista lógico universo y dios son equivalentes, es decir, todo lo que existe y pretende demostrarse su existencia bajo primer grado de subordinación.
Bueno, un agnóstico diría que Dios se plantea como un predicado, algo de lo que se habla o se predica. Por el contrario, un creyente lógico y no lógico diría que la divinidad es el sujeto pues cualquier cosa que se predique de la misma es una cualidad del ser divino: estrellas, planetas y criaturas biológicas son aspectos o determinaciones del ser divino, en este sentido no hay nada fuera de la divinidad. En el plano de la mística y la creencia no hay contradicción porque Dios es el sujeto universal, pero en el plano de la lógica el asunto no está tan claro, dependerá de si Dios es sujeto o predicado. Para Hegel el ser divino es un reflejo del mundo, esto conduce a formular un espíritu cultural que vertebre el debate sobre la divinidad conforme a ciertas reglas, no sólo racionales, también emocionales.
Tanto Hegel como Kant se percataron de las dificultades emocionales que tiene el acto de percibir al ser divino, la imposibilidad de acceder a la divinidad se constituye como represión y negatividad. Dado que ambos pensadores construyeron sus discursos filosóficos conforme a la lógica, se mostraron escépticos acerca de la mística y la creencia. Mientras que la fe implanta su discurso en la sociedad como un dato fáctico, irreversible y determinista, la lógica hegeliana transita el camino de la investigación de los conceptos que conducen a la divinidad. Esta vía es neutral y conciliadora con los aspectos racionales y emocionales de la personalidad humana, y por tanto también es tolerante con la fe religiosa. El escepticismo kantiano y hegeliano es posibilista, no se constituye como un a priori, y por tanto está abierto a la mística. El polo racional y religioso del debate tiene dos soluciones: el sectarismo subjetivista e inconmensurable de racionalistas y creyentes, o un marco común de diálogo que obedece a ciertas reglas discursivas donde la emoción forma parte del mismo.
Haber yo les demuestro que dios existe. Supongamos un video juego de computadoras digamos mario bro, que que tiene solo dos opciones, uno, ha diseñado por un programador o dos encierra en si mismo la causa de su propia existencia. Como concibira mario la existencia de un ser creador(programador), no puede siquiera imaginar como es, ya que el esta en una realidad virtual limitada por las reglas que ha.diseñado el programador. No entiende que el ,es un sofware, corriendo en un hardaware, y aunque tenga la nocion de correr y pasar mundos, realmente nunca pasa del pc de nuestro escritorio. Mario, nunca entendera lo que es realmente, porque solo tiene una autodefinicion para si mismo. Definicion dada por lineas de codigo creadas por el programador. Ahora bien. Aun cuando no exista un programador especifico que lo creo, y encierre en si mismo las causas de su propia existencia, entiende que puede aunque no pueda demostrarlo sistemas diferentes relaes o imaginarios compatibles o incompatibles a las reglas de su universo. Un cubo de 28 lados, es imposible, impensable para nosotros en el cual las reglas fisicas que nos gobiernan dictan que solo tienen 8 lados. Pero un sistema regido por reglas diferentes seria mas entendible tal cubo. Todo se reduce entonces a universo de posibilidades, despues de todo mario aun no sabe que nosotros jugamos con el .
Soy un joven de 17 años. Quisiera felicitarle por su artículo, me ha servido muchísimo y por ello también le doy las gracias. Me ha hecho gracia cuando he visto lo del libro de la biblioteca de Fuengirola, yo soy de ahí. Viva Fuengirola y enhorabuena por su trabajo!
Es posible considerar el conjunto de Dioses y probar q es de categorìa II?
Estaba viendo la estructura de la demostración, cada axioma, teorema y colorarios y no veo reglas de inferencia para lograr llegar a una deducción formal de la demostración del T4 o en el texto T3.
Si podrían el último paso sería increible.
Fuente: soy mátematico puro, anexo que soy cristiano así que no estoy en contra de la demostración.
Con todo respeto, si los comentarios solo son intentos por descollar en lógica matemática, estoy perdido y en el lugar equivocado. Solo deseo compartir mi percepción respecto a la lógica matemática y su relación con la idea de Dios. Más que la demostración ontológica de Gödel de la existencia de Dios, son sus teoremas de incompletitud los que prueban para siempre la existencia de verdades no demostrables. La implicación esencial de los teoremas es que la lógica formal, base de todas las ciencias, no puede demostrar de forma absoluta la existencia de Dios, pero tampoco puede demostrar su no existencia. Esa es una prueba absoluta de que la lógica es limitada. Pero los seres humanos por la causa que sea, somos capaces de trascender, al menos por intuición, los límites de la lógica formal; entonces para mí esta sola habilidad humana es la evidencia no formal de que tiene que existir un Algo universal, que aunque no demostrable desde la lógica, la contenga y sea superior a ella.
Es quien afirma la existencia de algo quien debe demostrarlo.
Me parece que tnto la demostración de Godel como su revisión computacional (https://arxiv.org/abs/1308.4526) deben tratarse como lo que son: demostraciones matemáticas. Lo que supone conceptualmente distinguirlo de sus consecuencias epistemológicas, que no son materia de ninguna de esas demostraciones. Ello porque lo que se haga tanto con la demostración de Godel como con su examen computacional a nivel de consecuencias epistemológicas, es asunto externo a las demostraciones. Decir que nada tienen que ver con el Dios cristiano (San Anselmo y Godel lo eran) es bastante atrevido, porque Anselmo no estaba haciendo un ejercicio con Pikachu. Realmente creía en Dios. Asunto distinto es que esas reflexiones queden en manos distintas, de filósofos o de teólogos (aunque nada impide convergencias de reflexiones, a fin de cuentas, todos los filósofos se ocuparon de Dios y muchos teólogos han sido grandes filósofos). Pero lo que no puede decirse es que la demostración de San Anselmo tratada por Godel es un tema irrelevante epistemológicamente hablando.
Cuando te basas en axiomas puedes demostrar que los burros vuelan. Muchos grandes científicos han demostrado que dios no existe (entre otros Hawkings).
Lo que comprueba esto, es que las mejores cualidades humanas están reflejadas por “necesidad” de tal aparente demostración, la “similitud” con el ser humano que la mayoría “esperaría ser” de sí mismo (quien acepta la “personalidad” asignada a Dios); y tal persona refleja quien en su pensamiento de forma “necesaria” lo acepta como tal sin entender el contenido más allá´de la simple idealización; básicamente.
No se puede confirmar o negar la existencia de lo que sea en referencia a DIos; las matemáticas solo explican lo que el ser humano alcanza a comprender como tal. Dios no es un ser humano; y eso es lo que siempre es consistente (necesidad), la posible incorporación «inconsciente» de tal abstracción. La mente humana (P) no es (Q) Dios. Por lo tanto, P no implica Q por «necesidad», sería una contradicción de «contenido necesario» (la primera) y solo para probar que así es (redundancia modal de una mente en expansión), por lo tanto una imposibilidad, pero no una contingencia, segunda contradicción.
Bueno, hasta esto tiene explicación, no «es» lo que se dice «es» en principio.
Y lo de pikachu es todavía más simplón en comparación. Aplicaría a todo personaje principal de cualquier cartoon de manera necesaria (al menos en la mayoría).
El ser humano no se cansa de buscar y creer que Dios esta al alcance de su comprensión «racional», lo cual por necesidad, es un absurdo, pero una «necesidad» inconsciente de su propia naturaleza (progreso), lo cual si es una contingencia, pero comprensible.
Dios no es una representación matemática, simple y sencillamente porque el ser humano refleja su humanidad en tal representación abstracta de Dios, su imperfección intrínseca. Es así de simple.
Me ha encantado el artículo por la forma en que queremos usar el raciocinio, la lógica, incluso la comparación:
«Si definimos que “el Papa es una persona que viste de blanco”, cualquier persona que vista de blanco sería el Papa, lo que es falso. Para definir al Papa tenemos que utilizar una propiedad esencial que le caracterice de forma unívoca; por ejemplo, “el Papa es el obispo de Roma”.
Es cierto que muchos tratamos de saber el por qué de las cosas y cómo funcionan, pero hay cosas que jamás tendrán un por qué y tenerle miedo a la falta de respuesta hace que muchos prefieran ser ateos, o como muchos científicos que prefieren la ciencia antes que la fe, pero por qué?, es una pregunta que no tendrá una respuesta clara por más que la llenes de palabras.
Esta es una historia de un periodista francés, Decoin, que cuenta una gran historia, que creo que hasta que no nos pase, es imposible que lo entendamos catolicoactivo com/dios-para-incrédulos/encontro-a-dios-cuando-pensaba-que-habia-encontrado-la-prueba-de-que-no-existia/, hay un por qué para esto?…. Qué lluevan las hipótesis!!!