Las redes de neuronas artificiales permiten obtener soluciones analíticas aproximadas a ecuaciones diferenciales. Usando un método variacional, la red determina los coeficientes de un desarrollo en serie que minimizan el residuo. Se publica en Science la resolución de la ecuación de Schrödinger de la mecánica cuántica en dos dimensiones para problemas multicuerpo usando este método. Se recurre a un esquema de aprendizaje con refuerzo para encontrar el estado fundamental de varias redes de espines (tipo Ising y Heisenberg). Además, se logra simular su evolución unitaria con el tiempo.
La red para aprendizaje profundo tiene capas ocultas, lo que ha hecho que algunos blogs sugieran una conexión con la interpretación de variables ocultas de la mecánica cuántica. Nada más lejos de la realidad. El nuevo método solo estudia la evolución unitaria (es decir, la evolución determinista en tiempo) de la función de onda, sin poder simular el proceso de medida, el (mal llamado) colapso de la función de onda y el comportamiento probabilístico del sistema cuántico. En lugar de usar un método de Montecarlo, un método en diferencias finitas, en elementos finitos o espectral, se usa una formulación variacional implementada con una red de neuronas artificiales de tipo Boltzmann. Por tanto, no hay ningún tipo de relación con las ideas de variables ocultas en mecánica cuántica.
El artículo es Giuseppe Carleo, Matthias Troyer, «Solving the quantum many-body problem with artificial neural networks,» Science 355: 602-606 (10 Feb 2017), doi: 10.1126/science.aag2302, arXiv:1606.02318 [cond-mat.dis-nn]. Más información en Michael R. Hush, «Machine learning for quantum physics,» Science 355: 580 (10 Feb 2017), doi: 10.1126/science.aam6564. No parece entender muy bien el logro, por lo exagerado de su pieza, Jennifer Ouellette, «AI learns to solve quantum state of many particles at once,» New Scientist, 09 Feb 2017; tampoco, pues menciona variables ocultas, entrelazamiento y espeluznante acción a distancia, John Timmer, «Neural network trained to solve quantum mechanical problems,» Ars Technica, 10 Feb 2017. Una pena, pues son reputados divulgadores.
El método variacional para resolver una ecuación diferencial en derivadas parciales es muy sencillo de explicar. Se toma un desarrollo en serie con n coeficientes indeterminados. Cada término de la serie cumple con las condiciones de contorno de la ecuación. Para un cierto valor de los coeficientes, la sustitución de la serie en la ecuación da un valor diferente de cero (porque no se cumple la ecuación, salvo que sea la solución exacta). Se considera que los coeficientes óptimos son los que minimizan dicho valor (calculado en cierta norma). Por tanto, resolver la ecuación consiste en resolver un problema de optimización. Las redes de neuronas artificiales son un método (tipo caja negra) muy usado para resolver este tipo de problemas.
Para obtener la evolución unitaria de la función de onda se usa una discretización del tiempo. Para cada paso de tiempo se resuelve el correspondiente problema de optimización, usando como aproximación a la solución la solución del paso de tiempo previo. El resultado de todos los métodos variacionales es asintótico, es decir, presenta un error que se acumula conforme pasa el tiempo. Por ello, aunque la solución inicial sea muy buena, conforme evoluciona va dejando de serlo. Lo que no quita que el método sea convergente, es decir, que con un paso de tiempo más pequeño (y mayor coste computacional) se logre un error menor.
En resumen, el que sepa algo de métodos numéricos o de redes de neuronas artificiales se preguntará como este artículo se ha publicado en la prestigiosa revista Science. Pero así son las cosas, la esperanza de publicar algo convencional en el top del top nunca se pierde.


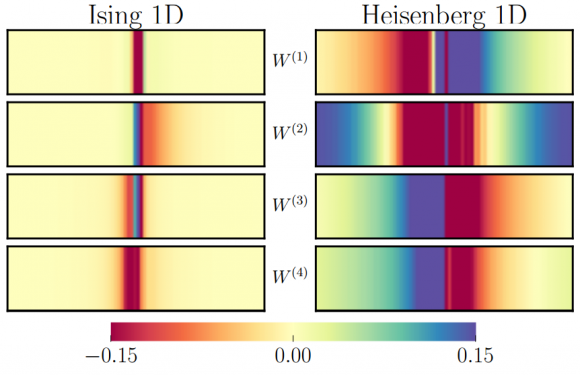
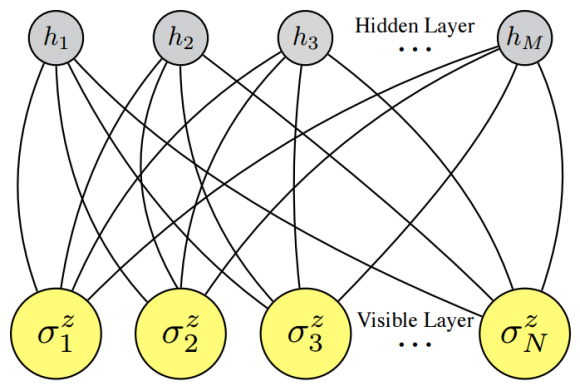


«…lo que ha hecho que algunos blogs sugieran una conexión con la interpretación de variables ocultas…» Madre mía, imaginación no falta, no.
La segunda dejación de variante, sin restar 2 tercios del 3 segmento, quiebra la unidad lineal.
Basta un simple quebrado y 2 incógnitas de Y más 0
No veo porqué no iba a publicarse…
Desde mi punto de vista, Alfonso, no tiene mucho sentido, por que se trata de una máquina de Bolztmann resolviendo ecuaciones diferenciales, que no es poco, pero no es novedoso.
Lo cañero hubiera sido que el sistema fuera capaz de resolver la primera parte, es decir, que dado un problema cualquiera, la máquina determinara como queda la ecuación de Schrödinger para esa realidad física, es decir, qué parámetros son qué en la ecuación; en este caso, la ecuación ya se le da, y lo que hace es resolverla.
Francis, la red de neuronas tipo Bolzman usada, ¿se trata de software simulando el comportamiento de la red de neuronas, o realmente se trata de una máquina, de un hardware con estados de energía reales etc…?
Perico, por supuesto, se trata de un software. Los autores del artículo dicen que le enviarán copia del software a quien lo solicite de forma justificada.
Hacía tiempo que no leía un artículo en el que no entiendo prácticamente nada de lo expuesto.
Supongo que mis conocimientos de diseñador no son lo suficientemente avanzados cómo para entender la mecánica cuántica a estos niveles. Me voy a estudiar un rato 😀