
Las ecuaciones de la teoría de cuerdas pueden ser una poderosa herramienta para analizar algunos estados exóticos de la materia, desde las bolas supercalientes de quarks y gluones, hasta los áltomos superfríos. El año pasado hubo cuatro conferencias internacionales que estimularon la colaboración entre físicos de cuerdas y físicos de la materia condensada. Los escépticos aún se preguntan si esta extraña alianza dará lugar a nuevas ideas o si solo es un matrimonio de conveniencia. La teoría de cuerdas predice la existencia de muchos nuevos estados de la materia, pero verificar estas predicciones es muy difícil y los experimentos decisivos aún están en fase de planificación. ¿Por qué muchos teóricos de cuerdas se dedican ahora a la física de la materia condensada? Dos libros publicados en 2006, «Not Even Wrong» de Peter Woit (no está traducido al español) y «The Trouble With Physics» de Lee Smolin (en español «Las dudas de la física en el siglo XXI»), dos libros que critican el alejamiento de la «teoría de todo» de los experimentos, podrían ser la causa psicológica del acercamiento de los teóricos de cuerdas hacia las aplicaciones en materia condensada en opinión de Joseph Polchinski, uno de los teóricos de cuerdas más famosos que trabaja en el Instituto Kavli de Física Teórica, Santa Bárbara, California. Nos lo ha contado Zeeya Merali, «Collaborative physics: String theory finds a bench mate,» Published online 19 October 2011 | News Feature, Nature 478: 302-304, 20 October 2011.
El noviazgo entre la teoría de cuerdas y la física de la materia condensada comenzó hace 12 años cuando Dam Thanh Son y Andrei Starinets se reunieron en 1999 en Nueva York. Ambos habían sido compañeros de habitación cuando eran estudiantes en la Universidad de Moscú en los 1980. Estos amigos habían perdido el contacto al abandonar Rusia tras la caída del muro. Cuando Son vió los cálculos en teoría de cuerdas de un alumno de doctorado de Starinets, Giuseppe Policastro, reconoció las mismas ecuaciones que él utilizaba para analizar un plasma de quarks y gluones. ¡Cómo era posible! Starinets le explicó que él y Policastro estaban trabajando en una idea propuesta en 1997 por Juan Maldacena, físico argentino que entonces estaba en la Universidad de Harvard en Cambridge, Massachusetts; Maldacena está ahora en el Instituto para Estudio Avanzado de Princeton, New Jersey. Las ecuaciones de Son para el plasma de quarks y gluones en un mundo tridimensional eran equivalentes gracias a la conjetura de Maldacena (correspondencia CFT/AdS o dualidad gauge/gravedad) a las ecuaciones de un campo gravitatorio tetradimensional, un mundo de partículas cuánticas tridimensional era equivalente a un mundo tetradimensional de agujeros negros y cuerdas. En realidad, en la versión original de Maldacena, esta equivalente entre una teoría gauge 4D y una teoría gravitatoria 5D.
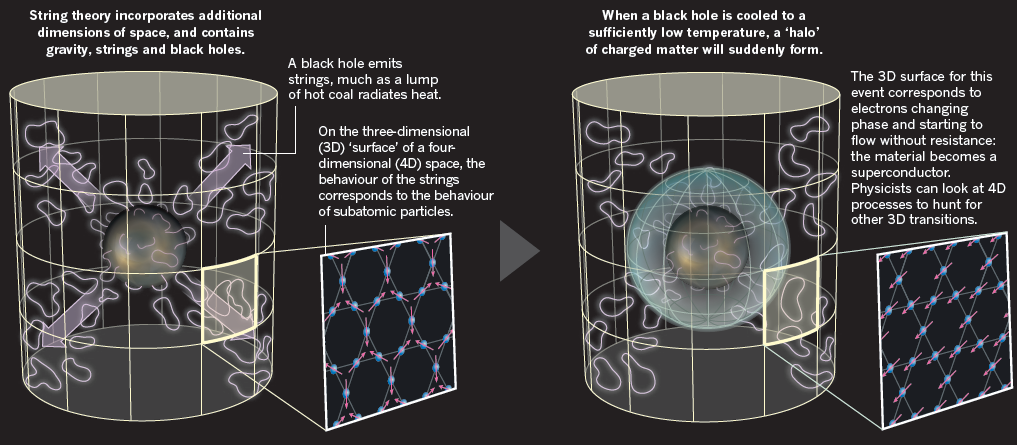
Son y Starinets observaron que que la correspondencia de Maldacena’s podía ser una herramienta matemática poderosa para resolver muchos problemas. En su caso concreto, cálculos cuánticos muy complicados en un plasma de quarks y gluones tridimensional podían ser transformados en cálculos muy sencillos en un espaciotiempo tetradimensional adecuado. Una vez obtenida la respuesta gravitatoria al problema, el resultado se podía escribir en el lenguaje de la teoría de campos. Los físicos de cuerdas dicen que hay un diccionario que relaciona los conceptos físicos entre ambas teorías. Son y Starinets lograron calcular la viscosidad (shear viscosity) de un plasma de quarks y gluones. En 2008, sus predicciones teóricas fueron confirmadas en el RHIC (Relativistic Heavy Ion Collider) en el BNL (Brookhaven National Laboratory), New York. Según un amigo de Son, este artículo fue «el primer artículo útil en teoría de cuerdas.»
Subir Sachdev, un teórico en materia condensada de Harvard, decidió aplicar la teoría de cuerdas al estudio de las transiciones de fase cuánticas (cambios que ocurren en un material a una temperatura muy próxima al cero absoluto cuando los efectos cuánticos empiezan a dominar). El estudio de estos estados exóticos de ciertos materiales, como superconductores de alta temperatura, superfluidos, condensados de Bose-Einstein y metales «extraños,» requería el desarrollo de nuevas herramientas matemáticas y resultó que en teoría de cuerdas dichas herramientas ya habían sido desarrolladas. Sachdev aplicó las ideas de Maldacena a materiales de laboratorio en dos artículos en 2007, uno publicado junto a Son y sus colegas, y otro junto a Sean Hartnoll, teórico de cuerdas de la Universidad de Stanford en California. Gracias a ello la conductividad en los metales extraños en 3D se hizo corresponder con ciertas propiedades de los agujeros negros en 4D, obteniendo resultados que reproducían los obtenidos en laboratorio. Problemas que habían sido imposibles de resolver en 20 años en la física de los metales extraños, parecían doblegados gracias a la teoría de cuerdas. Gracias a la gran reputación de Sachdev, muchos físicos de la materia condensada se empezaron a tomar en serio la necesidad de estudiar teoría de cuerdas.
Según Clifford Johnson, teórico de cuerdas de la Universidad de California del Sur, en Los Angeles, el resultado obtenido en materia condensada, al contrario que el obtenido en el plasma de quarks y gluones, incitó a muchos teóricos de cuerdas a cambiar de tópico, en lugar de estudiar la «teoría de todo» decidieron estudiar problemas físicos contrastables en laboratorio. «Como la miel que atrae a las abjeas,» muchos físicos jóvenes están siendo atraídos a estas nuevas aplicaciones de la teoría de cuerdas en física de la materia condensada. Según Polchinski «ya era hora de que la teoría de cuerdas se acercara a la realidad.» Todo esto tiene un grano de salAunque Polchinski también admite cierto punto de sal cuando afirma que «no creo que los teóricos de cuerdas hayan descubierto aún algo nuevo que los físicos de la materia condensada no supieran ya.» Aún pero, algunas predicciones de la teoría de cuerdas son muy «exóticas» para el punto de visto convencional en materia condensada y aún no han sido verificadas por los experimentos. Para convencer a los escépticos, los teóricos de cuerdas están buscando configuraciones de agujeros negros en teoría de cuerdas que predigan nuevas transiciones de fase aún no observadas por los físicos. Según Sachdev hay muchos problemas en materia condensada en los que se podrían encontrar este tipo de fenómenos.
Según Andrew Green, físico de la materia condensada en la Universidad de St Andrews, Gran Bretaña, todos estos descubrimientos muestran que hasta ahora la teoría de cuerdas ha sido mal interpretada, «tal vez la teoría de cuerdas no es una teoría única de la realidad, sino algo más profundo, un conjunto de principios matemáticos que pueden ser usados para relacionar todas las teorías físicas entre sí. Tal vez la teoría de cuerdas es el nuevo cálculo.»
Esta entrada es una contribución doble, por un lado a la «XXIV Edición del Carnaval de la Física,» hospedada en el blog de astronomía del argentino Gerardo Blanco «Últimas Noticias del Cosmos» (puedes enviar tus posts a «Últimas Noticias del Cosmos» hasta el 25 de octubre), por otro lado a la «Edición 2.7 del Carnaval de Matemáticas,» hospedada en el blog de Daniel Martín Reina «La Aventura de la Ciencia» (puedes enviar tus posts a «La Aventura de la Ciencia» hasta el 23 de octubre). Me gustaría haber escrito dos entradas diferentes… una para cada carnaval, pero ya veremos si me da tiempo, se me está echando el tiempo encima.


Genial entrada, y estoy totalmente de acuerdo, la teoría de cuerdas proporciona matemático un nuevo marco en el que entender procesos físicos reales. Quizás no hayamos llegado a la teoría del todo (afortunadamente en mi opinión) pero hemos aprendido muchas cosas nuevas que tendrán aplicaciones en distintos campos. Sólo por eso la teoría de cuerdas merece la pena.
Por cierto una pequeña errata (creo)… «correspondencia CDT/AdS» ¿no será CFT/AdS?
Gracias.
Yo me quedo con la cita de Andrew Green. Aunque no me gusta demasiado pensar que los científicos de la física quieran pasarse al cálculo alquímico de la álgebra teórica; espero que alguna teoría pueda condensar todo lo que sea del agrado de los experimentos pasados y futuros – aunque, a estas alturas, como dice un chiste informático: Si Dios tardó sólo 7 días en hacer el mundo eso es porque no tuvo que hacerlo compatible con una versión anterior.
Saludos y felicitaciones por la entrada.
Me temo que mucha gente que se ha saltado el calculo del siglo XX (y el del XIX), las homologias y cohomologias, los grupos de homotopia, invariantes topologicos, y hasta los tensores. Siempre me ha sorprendido que la gente encuentre sorprendentes los resultados matematicos de la teoria de cuerdas… ¡si se trata de barrer una seccion del espacio tiempo con una linea, en vez de un punto! Los geometras llevan un siglo haciendo eso, y no solo con lineas. Y los de cuerdas añaden un principio de accion muy particular, con lo que la teoria es en realidad mucho mas restringinda que la de los geometras. Es como si alguien dijera que «la teoria del tensor de curvatura de Riemann es el nuevo calculus»; te pierdes muchas cosas en ese punto de vista, pero es util para el estudio inicial de un objeto geometrico.
Estoy plenamente seguro de que el álgebra de los tensores tendrá que ser estudiada por neurólogos y psicólogos en un futuro no muy lejano.
Las matemáticas de la teoría de cuerdas y de otras ramas de la física no se restringen a homologías, homotopías, invariantes topológicos o tensores. No tiene nada que ver el tema de la acción. La matemática involucrada en las teorías físicas más en la frontera está en la frontera no sólo de la física sino también de la matemática. De hecho hay resultados en cuerdas que han servido para resolver problemas matemáticos, técnicas que provienen de la teoría cuántica de campos han sido útiles para la catalogación topológica de espacios de dimensiones bajas. Las técnicas espinoriales, los trabajos en geometría no conmutativa, geometría simpléctica, el estudio de algebras de Lie, afines, grupos cuánticos, etc, han venido motivadas y desarrolladas en gran parte por la física. Así que no está de más darle el valor que tiene a lo que hacen los físicos y a cómo la física genera nueva matemática, por ejemplo uno de los problemas más importantes es la de la justificación matemática de las integrales de Feynman. Los estudios derivados del operador de Dirac, incluso las distribuciones tuvieron su origen en la física.
A Witten le dieron la medalla Fields, y ya sabemos que eso se le da a avances matemáticos puros.
En fin, que la matemática es la matemática y la física la física, pero la matemática que nos ha traído la teoría de cuerdas no se restringe únicamente a herramientas previamente conocidas por los matemáticos.
El día que se encuentre una teoría -como la de cuerdas, sin ir mas lejos- en la que las partículas se muevan por mas dimensiones que las que conocemos…
…¡el mundo cuántico será determinista¡¡¡
Siempre he sido de la idea de que los fenómenos cuánticos son estadísticos porque las partículas se pasean por unas dimensiones fuera de nuestro alcance, y hacen y deshacen a su antojo, mas allá de nuestra capacidad de medir o calcular.
En un mundo en el que no existiera la tercera dimensión -digamos, la altura-, sus habitantes nos considerarían impredecibles porque éramos capaces de traspasar las paredes de su casa mediante un «curioso efecto túnel»: El simple hecho de pasar por encima de una raya pintada en el suelo.
Nunca podrían saber cuando íbamos a traspasar su pared, y por supuesto no serían capaces de percibirnos mientras nos desplazábamos por la tercera dimensión.
Abuela, mucho tiempo sin saber de tí por este foro… me alegra que vuelvas a comentar, porque tus comentarios siempre ponen los pies en la tierra y a este blog a veces le hacen falta.
En cuanto a lo que comentas sobre la posibilidad de que la teoría de cuerdas explique la mecánica cuántica, a modo de teoría de variables ocultas de la que observamos su comportamiento estadístico, te comento que muchos teóricos de cuerdas pensaban que algún día se podría lograr.
Pero la teoría de cuerdas clásica (relativista) es muy diferente a la teoría de cuerdas cuántica (y relativista), donde las cuerdas se rigen por las leyes de la física cuánfica. En la teoría clásica se admite un número arbitrario de dimensiones y hay muchísimos problemas (como la predicción de taquiones y la falta de unicidad). La teoría cuántica fija el número de dimensiones extra y resuelve casi todos estos problemas (incluso es «única» ya que hay solo 5 versiones duales entre sí). El problema de la versión cuántica es que asume como axiomas los de la mecánica cuántica y por tanto no puede predecir las reglas de la mecánica cuántica. Hacerlo sería como una pescadilla que se muerde la cola. Lo mismo le pasa a la versión en 11D (teoría M).
Saludos
Francis
Hola,
La teoria de cuerdas clasica no tiene «muchisimos problemas». De hecho, no tiene ninguno, es una teoria perfectamente bien definida, en cualquier numero de dimensiones. Asimismo no predice taquiones: la prediccion del taquion aparece cuando se cuantiza la Teoria de cuerdas bosonica, es un estado cuantico de la teoria bosonica.
En cuanto a la Teoria M, no se puede decir que utilice las reglas usuales de la mecanica cuantica para su cuantizacion, ya que nunca ha sido cuantizada. En concreto, la Teoria de Cuerdas se puede cuantizar porque la worldsheet es dos dimensional, pero en 11 dimensiones no hay cuerdas, hay otros tipos de membranas, cuya cuantizacion del worldvolume no ha sido lograda (aunque muchos papers se han escrito sobre ello).
Me hace gracia tu comentario, porque para explicar justo lo que comentas recurro a exactamente lo contrario:
– El hecho de que las partículas se entrelacen me da a pensar que conforman un sistema y con menos grados de libertad.
– Cuando un electrón se salta de su posición me da a pensar que tal vez se conformen por partes que no veo y que se intercambian sin tocarse.
– Cuando a una subpartícula le da por tomar dos direcciones a la vez, me da a pensar que esa subpartícula debe ser un conjunto de algo.
etc.
Lo siento, pero un universo que no sea plano no lo concibo.
Un momento, me perdí, ¿el universo es plano?
Eso es lo que pienso, principalmente porque antepongo un solo experimento a toda una amalgama de calibraciones.
Pero vamos, si un físico tiene que elegir entre las 4 dimensiones de Einstein y un modelo (que bien podría ser un álgebra de Lie, bien no tendría la obligación de serlo – porque el movimiento browniano no parece del todo compatible con las álgebras de Lie, pero claro, a lo mejor si se parte de un universo a gran escala sí se puede imponer el criterio de continuidad…, yo no sé) hecho por un menda, está claro.
En cualquier caso, sólo soy un mero informático. Cuando veo que algo no me convence mucho, pues simplemente lo digo. Malo sería que alguien haya expuesto fórmulas bastante concluyentes y que no se le haya hecho caso sólo por no estar afiliado a ninguna comunidad. Pero como yo ese mundo no lo conozco…
Contado así suena hasta bonito y todo, Pero, ¿no es y sería un tanto desolador que tuvieramos que recurrir a realidades inobservables a un nivel tan fundamental como la dimensionalidad del espacio?
No sé, el efecto túnel es una propiedad de las ondas. Se puede observar incluso con las huellas dactilares en un vaso lleno de agua, en el que se produce reflexión interna total, y sin embargo se pueden ver las huellas dactilares del dedo debido a las ondas evanescentes. No le veo ningun misterio, como tampoco veo misterio en que la materia sea inmaterial (curioso, ¿no?) y tenga cierta extensión espacial.
¿Que son las matemáticas? ¿Por que una herramienta «inventada» por los hombres describe tan detalladamente casi todos los fenómenos que existen en nuestro universo?
Como respuesta a la primera pregunta me gusta la que expone Keith Devlin en su libro «el lenguaje de las matemáticas»: «Las matemáticas son la ciencia de las estructuras. Las matemáticas estudian las características de estructuras abstractas: estructuras numéricas, de formas, de movimiento, de comportamiento, de repeticiones de sucesos aleatorios… Además estas estructuras pueden ser reales o imaginarias, visuales o mentales, estáticas o dinámicas, cualitativas o cuantitativas. Por ejemplo: la aritmética y la teoría de números estudian las estructuras de los números y del proceso de contar, la geometría las estructuras de las formas, el cálculo las estructuras del movimiento, la lógica estudia las estructuras del razonamiento, la probabilidad estudia las estructuras del azar y la topología las estructuras de la proximidad y la posición» Estas «estructuras» EXISTEN de alguna forma, algunas físicamente (como las formas o el movimiento) y otras de forma más abstracta (como los números o la lógica) pero es evidente que aunque ciertamente muchas «normas o reglas» de la estructura matemática son «inventadas» por los hombres, estas reglas están basadas en estructuras que existen en el universo INDEPENDIENTEMENTE DE LOS MATEMÁTICOS. Esto explicaría la segunda pregunta y porque nosotros (pobres mortales) tenemos acceso a través de las matemáticas a la explicación del comportamiento de las estructuras más profundas del universo.
Respecto a la teoría de cuerdas y la dualidad ADS/CFT (que es de lo que quería hablar XD) quiero decir lo siguiente: un mismo fenómeno físico puede ser descrito por varias formulaciones matemáticas distintas (y al revés una misma formulación matemática puede describir varios fenómenos físicos distintos). Estas dualidades permiten a los físicos-matemáticos elegir la formulación más adecuada que haga los cálculos más sencillos. Sin embargo uno podría preguntarse: ¿Que puñetas puede tener en común el comportamiento del plasma quark-glúon con el comportamiento de agujeros negros en dimensiones superiores? (hablando a groso modo). Evidentemente yo no se la respuesta sin embargo Lubos en su artículo «Perfect fluids, string theory, and black holes» nos da una pista de una posible relación (resumiendo muchísimo): el comportamiento del plasma quark-gluón como un líquido perfecto es consecuencia de un «acoplamiento fuerte». Este acoplamiento fuerte produce una disminución de los grados de libertad del sistema (un líquido tiene menos grados de libertad que un gas), a medida que se incrementa el acoplamiento fuerte se puede establecer un límite al que tiende el sistema y ese límite coincide precisamente con el comportamiento de un agujero negro que surge de «limitar» los grados de libertad del sistema (aunque represente de forma «dual» una situación de máxima entropía).
Absolutamente impresionante el poder de las matemáticas.
No veo la relación entre los teoremas de Gödel y la hipótesis «estas reglas están basadas en estructuras que existen en el universo INDEPENDIENTEMENTE DE LOS MATEMÁTICOS”, pues lo que demostró Gödel, hablando en forma aproximada, es que los sistemas formales no pueden quedar totalmente definidos, mientras que la hipótesis trata sobre la idea «platónica» de las matemáticas, vigente actualmente, creo que su mayor defensor es Roger Penrose.
Un sistema formal ya sabes que se basa en axiomas, teoremas y lógica bivalente; Gödel demuestra que siempre habrá teoremas indecidibles (quizá son ciertos, pero no podemos demostrarlos).
Por otro lado la idea platónica viene del hecho de la curiosa coincidencia entre descubrimientos matemáticos y naturaleza; por ejemplo, ciertos matemáticos, generalizando la geometría, van y enuncian las geometrias no lineales, que en principio eran meras construcciones abstractas sin relación alguna con la realidad, pero no mucho tiempo después resulta que se ajustan como un guante con la teoría de la relatividad general. Hay innumerables ejemplos como éste, en los primeros capítulos de «En busca de la realidad» de Penrose se defiende ésta visión platónica.
Así que, sinceramente, creo que has confundido nabos con patatas, por así decirlo.
Por otra parte el libro que recomiendas se ve interesante, aunque los detalles «vitales» de las humillaciones no me interesan para nada, no son ciencia, más bien son chismes.
Saludos
Por cierto Francis (perdón por salirme del tema) ¿Has oído los rumores de nueva física que proceden del análisis de datos de CMS? Se han detectado eventos con varios leptones y con pérdida de momento (alguna partícula ladrona) que no pueden ser explicados por el SM. Hay muchas posibilidades de que solo sea una fluctuación estadística pero otros como Lubos ya ven indicios de supersimetría. De todas formas habrá que estar atentos a estos resultados, si ATLAS los confirma sería espectacular.
A la hora de la verdad, el único que no va a estar en la fiesta del LHC, va a ser el invitado estrella: Mr. Higgs.
Tom, el álgebra es la algamasa de las interpretaciones físicas. Si sabes que ciertas operaciones experimentales cumplen alguna clase de simetría, puedes diseñar un operador que, a partir del ladrillo, pueda constituir un hermoso edificio.
El ejemplo más claro está en la física de Newton: experimentando con lo que pudo, nos endosó las ecuaciones diferenciales, que es el padrenuestro de lo macroscópico. De esta manera, si a través de las matemáticas, vemos una simetría que sólo se conocía experimentalmente, eso sería también un hallazgo: no una melodía compuesta por las mismas notas.
Lo malo que podemos tener algunos (espero que por mi limitación en matemáticas no me pase lo mismo) es pensar que la física es susceptible de poder interpretarse mediante nuestros lenguajes racionales basados en lo que vemos…, parece más evidente que debamos construir una notación especial (un álgebra) en base a cómo vemos que funcionan las cosas.
Por otro lado, cuando veo que dos naturalezas diferentes coinciden en el modelo yo lo que veo es, por definición, una simetría. Lo que quiere decir que podemos perfectamente incluir un grado de libertad sólo para definir la diferencia de esa naturaleza. O también, podemos decir que no es más que una mera casualidad. Nadie nos dice que nuestra teoría es la correcta, pero es posible que podamos explicar con una cosas que con la otra no se pueda.
Saludos.
Yo creo que es el nuevo Islam.
Tom, te ha hecho una pregunta – no te ha pedido que le cuentes tu vida. Cuando tu modelo crezca preséntalo en sociedad como un adulto.
Porque importa la aceleración relativa al observador. El electrón «puede pensar» que está siendo acelerado en lugar de estar en un campo gravitatorio, pero si tu lo ves en reposo, tú no ves radiación.
En primero de carrera veíamos que el campo magnético era un efecto relativista; el hermano de la estación verá el campo electromagnético de la carga en movimiento mientras que el observador del tren, en reposo respecto a la carga, solo verá el campo electrostático. Si nos movemos a la misma velocidad que las cargas de las corrientes se tienen que cumplir las leyes de la electrostática
El fotón cuando se mueve en un campo gravitatorio pierde energia, en la forma de disminución de la frecuéncia (corrimiento al rojo).
felicitaciones a todos…..son candidatos a trabajar en el CERN.
Hay un solo eterno que se divierte con su existencia-claro,la de
ustedes-y por si créen que no es así…lean salmos,en la biblia.
Miren….pa´sence un día leyendo Los Salmos,,,en la noche an-
tes de dormir…encomiéndense…..van a ver ustedes si al día
siguiente no van a tener soluciones….HAA!!! no dejen de tener
lápiz y papel a la mano…..copien inmediato al sueño.
gracias no se olviden de darlas…al eterno por supuesto.