La mayoría de los físicos expertos en superconductividad opinan que el modelo de Hubbard (1963) describe la superconductividad en los cupratos y otros superconductores no convencionales. Por desgracia, el modelo es tan complicado que aún no lo sabemos, ni siquiera si describe el efecto Meissner y otras propiedades superconductoras. Por fortuna, se acaba de publicar en Science que el modelo de Hubbard bidimensional dopado al 12.5% tiene un estado fundamental con electrones apareados y superconductividad de tipo d; así se confirma una conjetura abierta desde 1987. ¿Supone un paso relevante hacia la teoría definitiva de la superconductividad de alta temperatura? Aún no lo sabemos, aunque habrás oído que algunos medios así lo han proclamado.
El modelo ha sido resuelto numéricamente mediante una técnica llamada grupo de renormalización de la matriz densidad (DMRG); la diferencia con simulaciones previas es que se han usado 20 000 estados (un número mucho mayor que el usado en estudios previos). Se observan ondas de densidad de carga (CDW) y ondas de densidad de espín (SDW), pero no se observan ondas de densidad de pares (PDW). Tampoco se logran explicar otras propiedades de los superconductores no convencionales, como la resistividad lineal en función de la temperatura. Queda mucho trabajo de investigación pendiente en el estudio de los estados fuertemente correlados de este modelo de Hubbard para que se pueda afirmar que se ha dado un paso de gigante hacia la deseada teoría de la superconductividad hTc.
Habrá que estar al tanto sobre los progresos de este modelo (por cierto, tras su aparición en arXiv en junio de 2018 solo ha sido citado tres veces y de forma tangencial). El artículo es Hong-Chen Jiang, Thomas P. Devereaux, «Superconductivity in the doped Hubbard model and its interplay with next-nearest hopping t′,» Science 365: 1424-1428 (27 Sep 2019), doi: https://doi.org/10.1126/science.aal5304, arXiv:1806.01465 [cond-mat.str-el] (05 Jun 2018). Seguro que has leído a Javier Jiménez, «El secreto mejor guardado de la superconductividad estaba justo delante de nuestras narices: tras 33 años, empezamos a entenderla,» Xataka, 27 Sep 2019.

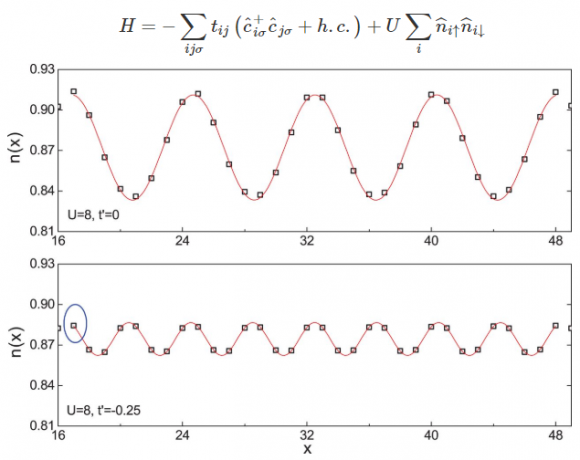
El modelo de Hubbard bidimensional asume que las cuasipartículas de tipo electrón (o hueco) están localizadas en ciertos lugares (sites) de la red cristalina del material, pudiendo saltar (hopping) entre estos. En cada sitio puede haber 0, 1, o 2 electrones; hay un electrón en el estado de neutralidad (aislante tipo Mott), hay dos electrones en el estado dopado con un electrón y hay cero electrones en el estado dopado con un hueco. En cada sitio los electrones están sometidos a una interacción coulombiana repulsiva descrita por la constante U. Además, existe cierta probabilidad tij de que un electrón salte entre los sitios i y j; en el modelo usado en el nuevo artículo en Science solo se considera el salto entre sitios vecinos (j=i±1), con probabilidad t, y el salto hasta el sitio más próximo a un vecino (j=i±2), con probabilidad t′ (el resto de los valores de tij son nulos).
Para simplificar las simulaciones por ordenador, se ha considerado una geometría cilíndrica para la red cuadrada (es decir, se han usado condiciones de contorno periódicas en una red rectangular con N = Lx × Ly sitios). En las simulaciones se ha considerado un dopado con huecos a una concentración δ = 12.5% en cilindros con Ly = 4 y Lx = 64. Se tomado un valor de referencia t = 1 y un valor t′ = −0.25 (que se comparado con t′ = 0), e interacciones U = 8 y U = 12. La magnetización se ha fijado a cero. Los interesados en más detalles sobre las simulaciones deben consultar la información suplementaria del artículo (así como un manual sobre simulacionas DMRG) [PDF].
La observación de stripes (tanto en CDW como en SDW) es la gran aportación de este nuevo trabajo. Todo indica que la interacción entre los órdenes superconductor y tipo stripe es la responsable de la sensibilidad de la superconductividad en el modelo de Hubbard estudiado al parámetro t′. Sin embargo, aún quedan muchas incógnitas por resolver antes de que se pueda proclamar que se ha avanzado hacia la teoría definitiva de la superconductividad no convencional de alta temperatura.


Hola, no sé si la pregunta es muy tonta pero, cual es el estado supercoductor en este modelo? Pares de electrones como en el modelo BCS? Han podido simular un estado superconductor los autores del artículo aparte de las ondas de densidad de carga y spin?
Angel, se ha calculado la función de correlación de pares (de Cooper), llamada Φ, que se muestra en la segunda figura de mi pieza Φyy (donde se muestra su valor en función de la longitud del cilindro Lx).
En simulaciones teóricas pasan muchas cosas, pero es necesario la comprobación mediante experimentos físicos. Teoría y práctica se deben encontrar.
Siempre he visto esto de la superconductividad, un tema muy complicado. Mucho más que la teoría microscópica de la ley de ohm, de los conductores eléctricos.
No se si hay alguna correlación entre las propiedades físicas de los materiales, a temperatura ambiente, con la temperatura crítica de superconducción; que nos permita conocer, si un trozo de material (una cerámica, un compuesto intermetálico, un carburo, un …), tendrá una Tc alta, o si esta será baja. Pero, desde que ha caido, el coeficiente de Hall (regla de Chapnik), como medida; y probablemente también el modulo de comprensibilidad (bulk modulus), y lafunción de trabajo (Work function). Apartir de ahora, será más difícil esta tarea.
En otro tema, https://francis.naukas.com/2014/02/23/grafeno-y-celulas-solares/ , he leído que » Los que trabajamos en efectos ópticos no lineales exóticos nunca perdemos la esperanza de que algún día se descubra un material con las propiedades que añoramos. Como no se pierde nada soñando, además nos gustaría que sus propiedades no lineales se observaran con luz de baja intensidad. Un futuro que, conforme uno envejece, parece más imposible cada día. Pero quien sabe, murallas más grandes han caído.»
¿ A qué murallas más grandes que ya han caído, te refieres? ¿Por que esta de óptica no lineal, más pequeña, no ha caído todavía?
No parece que, con la computación completamente óptica, se puedan contruir videoconsolas de juegos cuánticas, para videojuegos de tipo arcade 2D. Que mejoren en mucho a los actuales… Más bien, podrian recrear realidades artificiales o simuladas, como peliculas como Matrix, Tron, o la de las Holocubiertas de las películas de Star Trek. En fin, siempre nos quedará Pari…, esto, los ordenadores electrónicos, para videojuegos de tipo arcade 2D.