
La multiplicación C = A · B de dos matrices cuadradas n×n tiene un coste computacional de n3 productos y n3−n2 sumas con el algoritmo que multiplica filas por columnas (n productos y n–1 sumas) para obtener las n2 componentes del resultado. Usando la técnica de divide y vencerás se puede reducir el coste a nω productos con 2 < ω ≪ 3, incrementando el número de sumas; se aprovecha que la multiplicación de pequeñas matrices k×k se puede hacer con menos de k3 productos; el récord actual es ω = 2.3728596 de Alman y Williams (2020). Nature publica AlphaTensor, la nueva inteligencia artificial de DeepMind (Google), que descubre nuevos algoritmos de multiplicación de matrices que superan a los humanos. La mejora actual es pequeña, pero AlphaTensor ofrece nuevas ideas a los humanos sobre cómo construir nuevos algoritmos. Además, AlphaTensor puede minimizar el tiempo de ejecución del algoritmo en un microprocesador concreto; pues la latencia en ciclos de reloj de las operaciones de suma y producto en coma flotante depende mucho de la arquitectura interna del microprocesador, de su sistema de vectorización y de sus cachés de instrucciones y datos. AlphaTensor promete el algoritmo óptimo para un procesador concreto.
DeepMind empezó a desarrollar inteligencias artificiales para ganar a juegos Atari, al ajedrez y al go. Su idea con AlphaTensor es transformar el desarrollo de un algoritmo en un juego. Strassen (1969) desarrolló la representación tensorial del algoritmo para la multiplicación matricial (n,m,p) de matrices n×m y m×p dando una matriz n×p; consiste en tres matrices de n2×N, m2×N y p2×N con números en ℤ2 = {−1, 0 y 1} que representa el algoritmo con N productos. Combinando un algoritmo de Montecarlo que genera de forma aleatoria columnas de estas matrices, AlphaTensor juega a seleccionar la mejor para ganar el juego obteniendo el valor mínimo de N. AlphaTensor ha reproducido los mejores algoritmos humanos y mejorado algunos de ellos; para (4,4,4) y (5,5,5) su mejor algoritmo tiene 47 y 96 productos, cuando el mejor humano tenía 49 y 98, y para (4,4,5) y (4,5,5) usa 63 y 76, en lugar de 64 y 80. Por cierto, se ha publicado en arXiv un algoritmo para (5,5,5) que usa solo 95 productos gracias (en parte inspirado en el algoritmo de AlphaTensor).
AlphaTensor acaba de nacer y seguro que nos deparará muchas sorpresas en los próximos años. Además, seguro que podrá adaptarse a otros algoritmos de álgebra numérica, como la resolución de sistemas lineales o la factorización de matrices. Sin lugar a dudas las inteligencias artificiales ayudarán a muchos informáticos y matemáticos a desarrollar nuevos algoritmos. El artículo es Alhussein Fawzi, …, Demis Hassabis, Pushmeet Kohli, «Discovering faster matrix multiplication algorithms with reinforcement learning,» Nature 610: 47-53 (05 Oct 2022), doi: https://doi.org/10.1038/s41586-022-05172-4; más información divulgativa en «Artificial intelligence finds faster algorithms for multiplying matrices», Research Briefings, Nature (05 Oct 2022), doi: https://doi.org/10.1038/d41586-022-03023-w. El artículo sobre (5,5,5) es Manuel Kauers, Jakob Moosbauer, «The FBHHRBNRSSSHK-Algorithm for Multiplication in Z5×52 is still not the end of the story,» arXiv:2210.04045 [cs.SC] (08 Oct 2022), doi: https://doi.org/10.48550/arXiv.2210.04045.
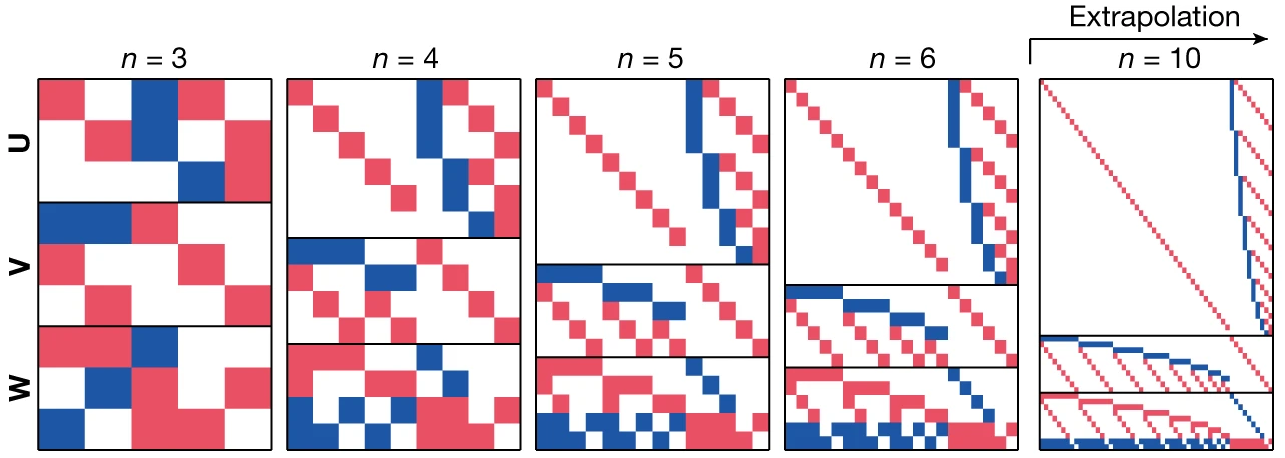
En mi opinión lo más relevante de AlphaTensor es que ofrece ideas novedosas sobre cómo construir nuevos algoritmos para la multiplicación de matrices. Para ayudar a los humanos lo mejor es colorear las tres matrices de la representación tensorial (U, V y W) con rojo (+1), azul (−1) y blanco (0). En esta figura se ha hecho para el producto de una matriz antisimétrica (A = −Aᵀ) por un vector; un matemático puede generalizar el patrón de colores observado para obtener un algoritmo para matrices de tamaño arbitrario.
Quizás te preguntas, ¿para qué sirve obtener algoritmos de multiplicación de matrices pequeñas? La idea es aprovechar la técnica divide y vencerás para diseñar algoritmos. En 1969, Strassen observó que para calcular el producto de dos matrices n×n podemos dividirla en cuatro submatrices (n/2)×(n/2) y aplicar un algoritmo para matrices 2×2 (implementado de forma que no se use que el producto es conmutativo); y para el producto de submatrices (n/2)×(n/2) podemos hacer lo diviéndolos en submatrices de (n/4)×(n/4); y así sucesivamente n/8, n/16, etc. hasta repetir el proceso log2(n) veces. La implementación más sencilla de este procedimiento es usar un algoritmo recursivo, como se presenta en el capítulo 4 de Cormen et al., «Introduction to Algorithms,» MIT Press (2009). Como el mejor algoritmo (2,2,2) usa 7 productos, en lugar de 8 (=23), con este algoritmo de Strassen se reduce el coste desde n3 hasta nω con ω = log2(7) = 2.807. El algoritmo de Strassen (wikipedia) se puede mejorar bastante usando una partición en un mayor número de bloques; por ejemplo, como (4,4,4) usa 47 productos en lugar de 64, el coste se reduce a nω con ω = log4(47) = 2.777.

Este tipo de algoritmos se puede mejorar mucho más en la línea del algoritmo de Coppersmith y Winograd de 1990 que redujo el coste hasta nω con ω = 2.3755; el mejor a día de hoy es el de Alman y Williams de 2020 con ω = 2.3728596. Como puedes ver en esta figura de la wikipedia, parece que la imaginación humana para desarrollar algoritmos de multiplicación de matrices ha alcanzado su límite. La opinión de muchos expertos no es que haya una obstrucción matemática detrás de este límite, sino que la causa es la explosión combinatoria en el número de posibles algoritmos. La gran conjetura abierta en Análisis Numérico es que el algoritmo óptimo podrá reducir el costo hasta ω = 2+ε, donde ε será muy pequeño (infinitesimal). Hay indicios indirectos que apuntan a que así debe ser, pero hasta ahora reducir el valor de ω está rayando lo imposible. Mi esperanza, y supongo que la de muchos expertos, es que AlphaTensor ofrezca nuevas ideas a los humanos expertos en el desarrollo de este tipo de algoritmos que permitan obtener ω < 2.37.

AlphaZero revolucionó el ajedrez, AlphaGo hizo lo mismo con el go; ambos juegan a nivel superhumano. Ahora mismo los grandes jugadores del ajedrez y del go estudian el juego de estas inteligencias artificiales para aprender estrategias novedosas que nunca se le ocurrieron a un humano. AlphaTensor ha logrado emular a los humanos sin usar ningún tipo de heurístico (igual que sus ancestros ganaban a los juegos de Atari sin saber qué era jugar a un juego Atari) y en algunos casos (en rojo en esta tabla) ha logrado superar a los humanos. No parece un gran éxito, pero AlphaTensor acaba de nacer y no se explotará todo su potencial hasta dentro de unos años.
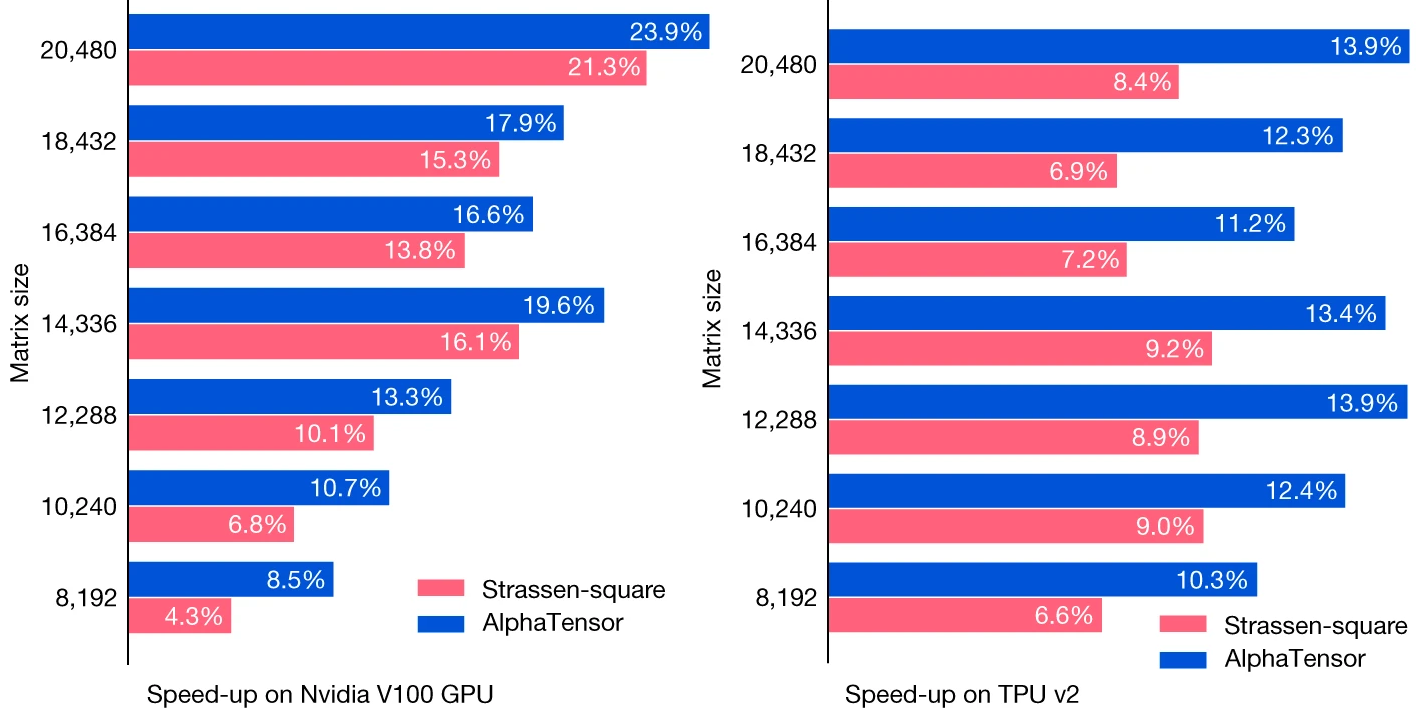
El algoritmo de Strassen y el mejor algoritmo de AlphaTensor para n = 213 = 8192 se han aplicado a matrices de tamaño n = 213 + m 211, con m = 0, 1, …, 6, es decir, n = 8192, 10240, …, 20480. En la figura se muestra el speed-up (la mejora en rendimiento) obtenida con el algoritmo de Strassen (en rojo) y el de AlphaTensor (en azul) tanto en una implementación en GPU como una en TPU; se observa que AlphaTensor obtiene una mayor mejora de rendimiento. La aplicación de AlphaTensor a algoritmos como el de Coppersmith y Winograd ofrecerá un speed-up aún mayor.
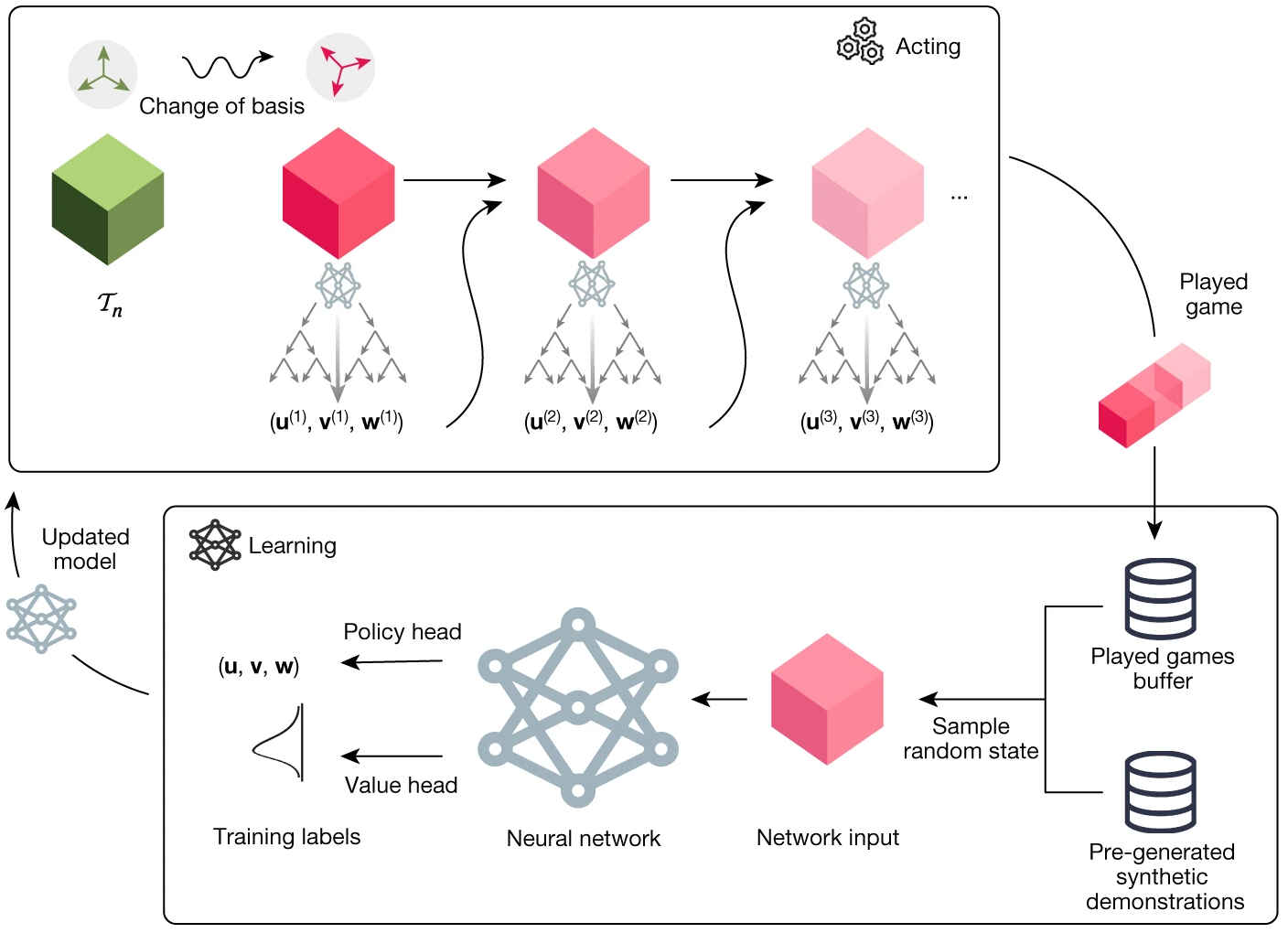
No entraré en los detalles del funcionamiento de AlphaTensor, que en rigor son poco novedosos. Lo que me gustaría destacar es que, igual que AlphaFold ha revolucionario la biología molecular, en los próximos años AlphaTensor promete revolucionar los algoritmos de álgebra numérica. Quizás lo más interesante es su flexibilidad a la hora de optimizar un algoritmo para una arquitectura concreta. Debo recordar que en las unidades de procesamiento numérico en coma flotante de los microprocesadores actuales hay muy poca diferencia en el coste (latencia en ciclos de reloj) de una suma y un producto (para tu procesador de Intel son 3 y 4 ciclos de reloj; una división es mucho más costosa, entre 5 y 12 ciclos de reloj); además, en el tiempo de ejecución influye mucho la jerarquía de la memoria y la comunicación de datos a través del bus.
En resumen, lo más interesante de AlphaTensor es el desarrollo de algoritmos que optimicen el tiempo real de ejecución de un algoritmo; de esta forma se desarrollarán algoritmos de álgebra numérica básica optimizados de forma específica para un ordenador concreto (que bien podría ser el tuyo). Esto podría ser realidad en pocos años y revolucionará la eficiencia de las simulaciones numéricas (como las necesarias en viodeojuegos, algo que agradecerán muchísimos los aficionados a los deportes electrónicos). Nos encontramos ante una revolución en ciernes.


Si no estamos en el punto de debatir y legislar la i.a poco faltará.
Entiendo que ninguna i.a trabajará con más información que la dispuesta por el ser humano para dicha i.a,
tambien es cierto que la i.a opera toda esa información de una manera menos sesgada, pudiendo obtener resultados diferentes, incluso mejores, pero tambien peores.
No sesgamos la información por gusto, es por superviciencia. Una i.a que no tiene los mismos sesgos no mira por nuestra supervivencia y bienestar, solo concluye cosas.
Dicho eso, Alphatensor es un claro ejemplo de buen uso de la i.a, ojalá mantengamos este rumbo, muy interesante pieza Francis.
Francis, en el mundo de los algoritmos para futuras computadoras cuánticas ¿Se ha desarrollado algún algoritmo que reduzca el clásico ω = 2+ε?
Sí, Pedro, hay algoritmos para multiplicar matrices binarias con un coste O(n^2) y para ciertas matrices especiales con coste o(n^2) . Pero aplicar dichos algoritmos al producto de matrices de números flotantes no parece prometedor. En mi opinión, nunca se usarán ordenadores cuánticos para multiplicar números en coma flotante.
Pero si transforman esos números de coma flotante en enteros de coma fija si no andan muy desparejos… luego solo hay que ajustar el punto decimal y listo. No será el mismo cálculo exacto pero sí aproximado…
Ojo, estoy preguntando, no afirmando.
Rfog, las operaciones en coma flotante están microprogramadas en la unidad de procesado de coma flotante integrada en el microprocesador; los nuevos algoritmos de multiplicación de matrices no tienen aplicación en los algoritmos microcableados (al menos por lo que yo he leído, debo confesar que estas cosas las estudié hace más de 30 años).
Pedro, parece que tienes en mente las películas de ciencia ficción como modelo de lo que pueden hacer las IA. Lo que aparece en las películas de ciencia ficción no será alcanzable con las IA durante este siglo. Y quizás nunca.
Justo no tenía en la mente ciencia ficción Francis, pensaba en el tema de los papers y que las i.a puedan escribir papers y pasar revisión por pares.
Me preocupa el filtro humano que debe existir entre las conclusiones de una i.a y la toma de acciones a partir de dichas conclusiones.
(Pero no me preocupa para cosas como Alphatensor, en este caso viene genial)
Pedro, ya hay IA que escriben papers y que han pasado una revisión por pares (laxa). En diez años serán indistinguibles un paper humano de uno de una IA. Ya se han desarrollado IA que detectan la producción de IA creativas. Pero el futuro de las IA creativas pasa por una ley que obligará a introducir «marcas de agua» que permitan diferenciar entre la producción creativa humana y la de las IA.
Francis, parece que se habla de la cota inferior del caso general A·B, pero parecería que haya speedups importantes al considerar la aparición de factores como 0 o K (k=1, …), o incluso relaciones menos obvias (m{i,j}=m{j,i}, …) que en la práctica son revisados en muchos algoritmos para aplicar una u otra estrategia (sin pretender cubrir un caso general u óptimo, tan sólo práctico). Parecería entonces que no sólo para una arquitectura concreta, sino que, podría obtenerse un algoritmo adaptativo que en la práctica rebajara el valor de ω aún más. ¿Hay trabajos al respecto o no merece la pena ese tipo de optimizaciones en la práctica?
Gracias Francis por tus entradas.
Josejuan, la estructura de la matriz es clave para la optimización de algoritmos de álgebra numérica (de hecho, casi la totalidad de las matrices usadas en ingeniería y ciencia tienen estructura). Hay muchísimos trabajos sobre este tema y por supuesto que merece la pena en la práctica. Por ejemplo, para una matriz dispersa (sparse) con O(n) elementos no nulos el coste computacional de las operaciones matriciales es O(n).
Me parece relevante el párrafo siguiente para elucidar los límites de la IA:
AlphaTensor ha logrado emular a los humanos sin usar ningún tipo de heurístico (igual que sus ancestros ganaban a los juegos de Atari sin saber qué era jugar a un juego Atari) y en algunos casos (en rojo en esta tabla) ha logrado superar a los humanos.
Saber o no saber que se está jugando o a qué se está jugando es la clave de vuelta. En este sentido buenas son todavía las opiniones de Turing.
Saludos
«Saber o no saber que se está jugando o a qué se está jugando es la clave de vuelta.»
Y si jugáramos tú y yo ¿cómo tú sabrías que yo lo se?
Y otra duda, Francis, ¿Se ha conseguido modelizar un juego para IA tal que ésta se dedicara a optimizar algún problema de tipo NP, por si sonara la flauta y lo resolviera en un tiempo polinomico?
Pedro, el problema de diseñar nuevos algoritmos de multiplicación de matrices es un problema NP. Y no, ninguna IA, logrará un imposible (aunque aún no haya sido demostrado matemáticamente).
Ostras, claro…es NP
Hola Francis. Como siempre es un placer leerte y también escucharte en directo, como he podido comprobar en persona. Respecto a este tema, no acabo de entender la razón por la cual en la medida de complejidad algorítmica únicamente se hace referencia al número de productos. Tal y cómo bien explicas, no hay tanta diferencia entre productos y sumas, por lo que una medida (rank) más adecuada quizás sería una ponderación de productos y sumas, en vez de usar únicamente los productos.
Nacho, la razón es que la técnica divide y vencerás del algoritmo de Straseen se basa una recursión sobre los productos. Por ello se considera el producto como la operación clave.
Francis, crees que la IA será capaz de resolver algunos de los grandes problemas de la matemática de manera autónoma durante este siglo? Algún problema del Milenio o de la lista de Smale o aún estamos lejos de ese punto? Llegaremos algún día?
No, Paco, creo que ninguna IA resolverá uno de esos problemas. Obviamente, espero equivocarme, pues la mayoría de estos problemas no serán resueltos en el siglo XXI y me gustaría poder estudiar la demostración de todos ellos.
Entiendo que una ia no puede resolver lo que las matemáticas no puede resolver.
Al igual sucede en el juego de la vida de conway, puedes emular la criba de eratóstenes generando todos los números primos y pensar ingenuamente que entonces el juego debe poder expresar la distribución de los primos, pero no, no existe ninguna condición inicial y posterior patrón que describa la distribución de los primos dentro del juego.
Pedro, las IA actuales no razonan, solo buscan en un gran espacio de soluciones la mejor para un problema dado; de hecho, necesitan ejemplos de resultados posibles como guía (el llamado entrenamiento); así es imposible obtener la demostración matemática de problemas realmente difíciles. En un futuro, quizás dentro de unas décadas, las IA serán capaces de razonar, lo que les guiará en la exploración del espacio de soluciones; sin embargo, no creo que puedan prescindir de los ejemplos de resultados posibles (del entrenamiento); por ello no creo que sean capaces de obtener la demostración matemática de problemas realmente difíciles (cuya demostración es única y completamente diferente de todas las demostraciones matemáticas previas; en la mayoría de los casos estas demostraciones requieren crear una nueva área de las matemáticas, con lo que no existen teoremas y demostraciones previas en dicha área inexistente).
Hace un par de coffe breaks, Francis, hablabas del superdeterninismo; no sé si hay visto esta joyita de Hossenfelder , donde nos devela que físicos como Nicolas Gsin o Zellinger no tienen ni idea de lo que implica realmente las desigualdades de Bell, y obviamente Bell tampoco se enteraba. 7000 comentarios de agradecidos legos. Aviso: Hay que estar relajado para verlo.
https://youtu.be/ytyjgIyegDI
Pedro, le leí hace tiempo en «Does Superdeterminism save Quantum Mechanics? Or Does It Kill Free Will and Destroy Science?» http://backreaction.blogspot.com/2021/12/does-superdeterminism-save-quantum.html Sabine se apropia del término introducido por Bell, pero lo redefine a su manera (que difiere de la original de Bell y la posterior de otros). En cualquier caso, esto es muy sencillo, te convence Sabine y aceptas su redefinición, o no te convence y no la aceptas. No hay más que discutir. En mi opinión, lo que opine Sabine es irrelevante.
Sí, tienes toda la razón, pero lo doloroso son las formas torticeras…el problema no es su opinión, ni sus papers, todo eso es física, es la manipulación aprovechando una posición de autoridad que da el estar dentro del mundo académico.